Завдання 603
Вісімдесят тисяч (80 000); сто сорок тисяч (140 000); двісті п'ять тисяч (205 000); шістсот тисяч триста (600 300); шістсот тисяч (600 000); тридцять тисяч тридцять (30 300); сімсот сімдесят сім тисяч сімдесят сім (777 077)
Нулі в записах чисел означають відсутність розрядів.
600 000 = 6 сот. тис.
30 300 = 3 дес. тис + 3 сот.
777 077 = 7 сот. тис. + 7 дес. тис. + 7 од. тис. + 7 дес. + 7 од.
Завдання 604 Сума розрядних доданків
70 000 + 3000 + 800 + 20 + 5 = 73 825
600 000 + 10 000 + 6000 + 60 + 8 = 616 068
400 000 + 30 000 + 100 + 10 + 4 = 430 114
20 000 + 400 + 6 = 20 406
30 000 + 50 + 3 = 30 053
80 000 + 800 + 8 = 80 808
Завдання 605 Числа, які розташовані в натуральному ряді між числами.
2 980 і 2 100 (2 981, 2 982, 2 983, …, 2 097, 2 098, 2 099)
5 596 і 5 604 (5 597, 5 598, 5 599, …, 5 601, 5 602, 5 603)
30 520 і 30 525 (30 521, 30 522, 30 523, 30 524)
42 389 і 42 393 (42 390, 42 391, 42 392)
415 997 і 416 002 (415 998, 415 999, 416 000, 416 001)
8 997 і 9 000 (8 998, 8 999)
Завдання 606
|
80000 + 320 = 80320 8000 + 137 = 8137 51000 + 951 = 51951 |
70338 – 338 = 70000 70338 – 70000 = 338 70338 – 70338 = 0 |
200000 • З = 600000 100000 • 8 = 800000 600000 : 2 = 300000 |
Завдання 607
76 249 – 249 = 76 тис. 249 од. – 249 од. = 76 тис. = 76 000
84 311 – 84 000 = 84 тис. 311 од. – 84 тис. = 311 од. = 311
324 432 – 324 000 = 324 тис. 432 од. – 324 тис. = 432 од. = 432
Завдання 608
|
Місткість бідона |
Кількість бідонів |
Загальна місткість |
|
9 л |
? |
810 л |
|
? |
?, на 9 менше |
стільки само |
До супермаркету привезли 810 л молока у малих бідонах по 9 л. Стільки само молока привезли у великих бідонах. Яка місткість великого бідона, якщо їх привезли на 9 бідонів менше, ніж малих?
Розв’язання
1) 810 : 9 = 90 (б.) – малих бідонів
2) 90 – 9 = 81 (б.) – великих бідонів
3) 810 : 81 = 10 (л.)
Відповідь: місткість великого бідона 10 літрів.
|
Місткість бідона |
Кількість бідонів |
Загальна місткість |
|
? |
?, на 9 більше |
стільки само |
|
10 л |
? |
810 л |
До супермаркету привезли 810 л молока у великих бідонах по 10 л. Стільки само молока привезли у малих бідонах. Яка місткість малого бідона, якщо їх привезли на 9 бідонів більше, ніж великих?
Розв’язання
1) 810 : 10 = 81 (б.) – великих бідонів
2) 81 + 9 = 90 (б.) – малих бідонів
3) 810 : 90 = 9 (л)
Відповідь: місткість одного малого бідона 9 літрів.
Завдання 609
|
Місткість |
Кількість упаковок |
Всього упаковок |
Загальна місткість |
|
|
Вода |
8 пл. |
? |
?
|
720 пл |
|
Сік |
9 пл. |
?, у 2 рази менше |
стільки само |
Розв’язання
1) 720 : 8 = 90 (уп.) – упаковок води
2) 720 : 2 = 360 (пл.) – пляшок соку
3) 360 : 9 = 40 (уп.) – упаковок соку
4) 90 + 40 = 130 (уп.)
Відповідь: 130 упаковок води і соку привезли до магазину.
10 • 10 • 10 < 100 • 100 (хибна числова нерівність 1000 < 10 000)
743 + 159 > 1 000 – 97 (хибна числова нерівність 902 > 903)
3 050 – 50 < 20 000 + 10 000 (істинна числова нерівність 3 000 < 30 000)
2 700 + 1 300 = 4 000 (числова рівність)
Відомо, що маса 1 л чистої води дорівнює 1 кг. Чому дорівнює маса 10 л води? 100 л? 1000 л? 2000 л? 50 000 л?
|
1 л = 1 кг
10 л = 10 кг
|
100 л = 100 кг
1000 л = 1000 кг
|
2000 л = 2000 кг
50000 л = 50000 кг
|
Яку частину тонни становить маса 500 л води? 50 л? 10 л?
|
500 л = 1/2 т
|
50 л = 1/20 т
|
10 л = 1/100 т
|
Скільки тонн важить 40 000 л, 80 000 л, 700 000 л води?
|
40000 л = 40 т
|
80000 л = 80 т
|
700000 л = 700 т
|
Завдання 612
|
100 = 99 + 1 100 = 90 + 10 1000 = 999 + 1 1000 = 990 + 10 1000 = 900 + 100 |
10000 = 9999 + 1 10000 = 9990 + 10 10000 = 9900 + 100 10000 = 9000 + 1000 |
100000 = 99999 + 1 100000 = 99990 + 10 100000 = 99900 + 100 100000 = 99000 + 1000 100000 = 90000 + 10000 |
Завдання 613
|
Ціна |
Маса |
Вартість |
|
|
Персики |
35 грн |
? |
однакова
|
|
Яблука |
?, на 7 грн менша |
20 кг |
Розв’язання
1) 35 – 7 = 28 (грн) – ціна яблук
2) 28 • 20 = 560 (грн) – вартість яблук (персиків)
3) 560 : 35 = 16 (кг)
Відповідь: купили 16 кілограмів персиків.
Дослідження.
Кількість базових (основних) слів, щоб назвати будь-яке натуральне число в межах мільйона: 13 (один, два, три, чотири, п’ять, шість, сім, вісім, дев’ять, десять, сто, тисяч, мільйон).
Примітка Одинадцять, двадцять — такі слова похідні з уже відомих базових слів, тому їх не пишемо.
Від 7 до 15 (7, 8, 9, 10, 11, 12, 13, 14, 15)
Від 90 до 113 (90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113)
Від 230 до 249 (230, 231, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249)
Від 1 058 до 1 064 (1058, 1059, 1060, 1061, 1062, 1063)
Від 2 058 до 2 064 (2058, 2059, 2060, 2061, 2062, 2063, 2064)
Від 10 058 до 10 064 (10058, 10059, 10060, 10061, 10062, 10063, 10064)
Від 3 333 до 3 325 (3333, 3332, 3331, 3330, 3329, 3328, 3327, 3326, 3325)
Від 4 997 до 5 007 (4997, 4998, 4999, 5000, 5001, 5002, 5003, 5004, 5005, 5006, 5007)
Від 100 до 200: 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200
Від 500 до 400: 500, 490, 480, 470, 460, 450, 440, 430, 420, 410, 400
Від 4000 до 4150: 4000, 4010, 4020, 4030, 4040, 4050, 4060, 4070, 4080, 4090, 4100, 4110, 4120, 4130, 4140, 4150
Від 2000 до 1970: 2000, 1990, 1980, 1970
Від 25 800 до 26 050: 25800, 25810, 25820, 25830, 25840, 25850, 25860, 25870, 25880, 25890, 25900, 25910, 25920, 25930, 25940, 25950, 25960, 25970, 25980, 25990, 26000, 26010, 26020, 26030, 26040, 26050
Від 40 060 до 40 000: 40060, 40050, 40040, 40030, 40020, 40010, 40000
2 сот. З дес. 5 од. = 200 + 30 + 5 = 235
5 тис. 2 сот. З дес. 5 од = 5 000 + 200 + 30 + 5 = 5 235
4 дес. тис. 5 тис. 2 сот. З дес. 5 од. = 40 000 + 5 000 + 200 + 30 + 5 = 45 235
6 тис. 4 сот. 2 дес. З од. = 6 000 + 400 + 20 + 3 = 6 423
7 дес. тис. 6 тис. 4 сот. 2 дес. З од. = 70 000 + 6 000 + 400 + 20 + 3 = 76 423
4 сот. тис. 7 дес. тис. 6 тис. 4 сот. 2 дес. З од. = 400 000 + 70 000 + 6 000 + 400 + 20 + 3 =
= 476 423
Найбільше число: 476 423, бо має найбільшу кількість розрядних одиниць.
1) 1 234 > 1 233, бо число 1 234 йде після 1 233.
2) 31 105 > 3 110, бо число 31 105 має більше цифр.
3) 42 229 < 42 230, бо більше одиниць старшого розряду.
|
77 324 > 67 324 |
25 504 < 26 504 |
2451 < 2452 |
Завдання 620
38 – х > 25, якщо х = 0, 1, 2, 3, 4
425 – х > 415, якщо х = 0, 1, 2, 3, 4
у • 3 < 30, якщо у = 0, 1, 2, 3, 4
у • 4 < 80, якщо у = 0, 1, 2, 3, 4, 5
х : 5 > 4, якщо х = 21, 22, 23, 24, 25
х : 10 < 5, якщо х = 0, 1, 2, 3, 4, 5
Для шкільної бібліотеки закупили 12 українсько-англійських словників, по 60 грн кожний, і 15 українсько-французьких словників, по 55 грн кожен. Вартість яких словників більша і на скільки? Запиши розв’язання задачі виразом.
Вираз: 55 • 15 – 60 • 12 = 105 (грн)
Відповідь: на 105 гривень більша вартість українсько-французьких словників, ніж українсько-англійських словників.
|
5300 – 300 = 5000 7800 – 7 000 = 800 4250 – 4 200 = 50 |
9000 – 2000 = 7000 24200 – 24000 = 200 10999 – 10990 = 9 |
40075 – 75 = 40000 637150 – 37150 = 600000 110000 + 13000 = 123000 |
Завдання 623
794 < 1□□□ (більше цифр)
24□□ > 19□□ (більше одиниць старшого розряду)
7□□□□ > 8□□□ (більше цифр)
654□ < 655□ (менше одиниць старшого розряду)
1□□□ > □99 (більше цифр)
3□□□ < 39 999 (менше цифр).
Для ремонту бібліотеки купили 7 однакових банок фарби, по 49 грн кожна, і 11 однакових банок лаку, по 57 грн кожна. Яка вартість усієї покупки?
Розв’язання
1) 49 • 7 = 343 (грн) – вартість фарби
2) 37 • 11 = 407 (грн) – вартість лаку
3) 343 + 407 = 750 (грн)
Відповідь: вартість усієї покупки 750 гривень.
Склади обернену задачу, у якій шуканим було б число 57.
Для ремонту бібліотеки купили 7 однакових банок фарби, ціною по 49 грн кожна, і 11 однакових банок лаку. Яка ціна лаку, якщо вартість усієї покупки рівна 750 гривень?
Розв’язання
1) 49 • 7 = 343 (грн) – вартість фарб
2) 750 – 343 = 407 (грн) – вартість лаку
3) 407 : 11 = 37 (грн)
Відповідь: ціна лаку 37 гривень.
Центр кола, яке доторкається до сторін квадрата, знаходиться в точці перетину діагоналей квадрата.
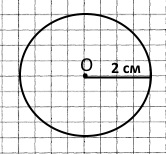
Радіус такого кола дорівнює половині сторони квадрата: 4 см : 2 = 2 см.