Інші завдання дивись тут...

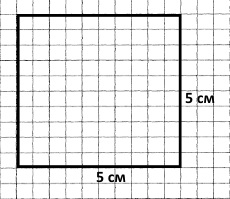
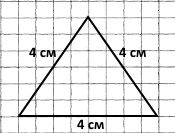
Завдання 621 Запиши дробовим числом, яка частина фігури зафарбована.

2/6, 1/4, 1/2, 3/8 

 

Завдання 622 Дроби в порядку зростання: 

1/200, 2/200, 5/200, 10/200, 20/200, 50/200, 100/200, 200/200

 

Завдання 623

а) що більше: 1/2 від 10 см чи 1/5 від 10 см;

1/2 від 10 см = 10 см : 2 = 5 см

1/5 від 10 см = 10 см : 5 = 2 см

1/2 від 10 см > 1/5 від 10 см

б) що менше: 1/3 від 300 кг чи 1/4 від 300 кг.

1/3 від 300 кг = 300 кг : 3 = 100 кг

1/4 від 300 кг = 300 кг : 4 = 75 кг

1/3 від 300 кг > 1/4 від 300 кг

Інше виконання: 1/2 > 1/5, 1/3 > 1/4

 

Завдання 624

Для оздоблення сцени шкільного театру використали 16 мотків кольорових стрічок. Мотків червоного кольору було 1/8, блакитного — 3/8 від числа усіх мотків, а решта мотків — зеленого кольору. Скільки зелених мотків використали для оздоблення сцени?

Розв’язання

1) 16 : 8 • 1 = 2 (м.) — червоного кольору

2) 16 : 8 • 3 = 6 (м.) – блакитного кольору

3) 6 + 2 = 8 (м.) – червоного і блакитного кольору разом

4) 16 – 8 = 8 (м.) – зеленого кольору

Відповідь: для оздоблення сцени використали 8 зелених мотків стрічок.

 

Завдання 625

3/8 від 16 = 16 : 8 • 3 = 6

3/5 від 60 хв = 60 хв : 5 • 3 = 36 хв

4/10 від 1 км = 1000 м : 10 • 4 = 400 м

 

Завдання 626

1) За схематичним рисунком і записом другої дії № 624 поясни, як знайти величину дробу від цілого.

2) Спробуй прочитати математичне твердження, записане латинськими буквами.

Щоб знайти значення a/b від с, потрібно с поділити на b, а потім результат помножити на а.

 

Завдання 627

а) Урок у першому класі тривав 7/12 год. Скільки хвилин тривав урок?

7/12 год = 60 хв : 12 • 7 = 35 хв – тривалість уроку в першому класі

б) Урок у сьомому класі тривав 3/4 год. На скільки хвилин довше тривав урок у сьомому класі, ніж у першому?

3/4 год = 1 год : 4 • 3 = 60 хв : 4 • 3 = 45 хв – тривалість уроку в сьомому класі

45 – 35 = 10 (хв) – на скільки хвилин довше тривав урок у сьомому класі

 

Завдання 628

Відстань між Харковом і Луганськом 330 км. 4/11 цього шляху автомобіль проїхав зі швидкістю 60 км/год. Скільки годин автомобіль був у дорозі, якщо решту відстані він їхав зі швидкістю 70 км/год? З’ясуй, чи правильно складено схему за текстом задачі. Які найменування потрібно дописати біля числових даних?

Розв’язання

1) 330 : 11 • 4 = 120 (км) – проїхав зі швидкістю 60 км/год

2) 120 : 60 = 2 (год) – був у дорозі до зміни швидкості

3) 330 – 120 = 210 (км) – решта відстань

4) 210 : 70 = 3 (год) – час подолання решти шляху

5) 2 + 3 = 5 (год) – час у дорозі.

Відповідь: автомобіль був у дорозі 5 год.

 

Завдання 629

Білка може стрибнути в довжину на 14 м, а кінь — на 4/7 цієї довжини. Чому дорівнює довжина стрибка коня? 

^{Короткий запис}

^{Білка — 14 м}

^{Кінь — ?, на 4/7 довжини}

Розв’язання

14 : 7 • 4 = 8 (м)

Відповідь: довжина стрибка коня 8 метрів.

Порівняй цю відстань з шириною твого класу чи твоєї кімнати. Ширина моєї кімнати 4 м — це у два рази менше, ніж довжина стрибка коня. 

 

Завдання 630

Побудуй круг, радіус якого 2 см. Проведи в ньому діаметр AB. З’єднай будь-яку точку C кола з кінцями діаметра.

Яка фігура утворилася? Утвориться трикутник.

Знайди периметр утвореної фігури. Периметр утвореного трикутника дорівнює сумі 4 см і довжин двох інших сторін.

 

Завдання 631

Пінгвін може перебувати під водою 18 хв, а морж — 5/9 цього часу. На скільки довше перебуває під водою пінгвін, ніж морж?

Розв'язання

1) 18 : 9 • 5 = 10 (хв) – час під водою для моржа

2) 18 – 10 = 8 (хв)

Відповідь: на 8 хв довше перебуває під водою пігнвін, ніж морж.

 

Завдання 632

Практична робота.

Тема. Моделювання цілого з його частин.

Обладнання. Аркуші кольорового паперу, циркуль, олівець, лінійка, ножиці.

Хід роботи

1) Побудуй круг, радіус якого 5 см.

2) Виріж його. Зроби ще 4 копії таких кругів.

3) Розріж кожний круг навпіл. Скільки половинок кругів утворилося? 10

5 • 2 = 10

4) Чи може бути 2 однакові половинки? 4, 5, 10 однакових  половинок? Може бути

5) Чи можна твої відповіді записати так? Можна

6) Спробуй з 10 половинок знову скласти круги. Отримаємо 5 кругів.

7) Скільки цілих кругів можна скласти з 9 половинок? Чотири цілих і половину або 4 і 1/2.

9 : 2 = 4 (ост. 1)

 

Завдання 633 Прочитай дробові числа

1/2 (одна друга); 1/6 (одна шостих); 3/6 (три шостих); 5/6 (п'ять шостих) ;  6/6 (шість шостих);  12/6 (дванадцять шостих)

 

Завдання 634

Довжина стрибка звичайної білки 15 м, це становить 1/4 довжини стрибка білки-летяги. Чому дорівнює довжина стрибка білки-летяги?

^{Короткий запис}

^{Білка — 15 м, це становить 1/4 довжини}

^{Кінь — ?}

Розв’язання

15 : 1 • 4 = 60 (м)

Відповідь: довжина стрибка білки-летяги 60 м.

 

Завдання 635

Маса 3/4 кавуна 9 кг. Яка маса цілого кавуна?

Розв’язання

1) 9 кг : 3 = 3 кг — маса 1 частини кавуна.

2) З кг • 4 = 12 кг

Відповідь: маса цілого кавуна 12 кг.

 

Завдання 636

У пасажирському потязі є 12 купейних вагонів, що становить 2/3 усіх вагонів, решта — плацкартні. Скільки плацкартних вагонів у потязі?

^{Короткий запис}

^{Купейних — 12 в., це становить 2/3 усіх вагонів}

^{Плацкартних — ?, решта}

Розв’язання

1) 12 : 2 • 3 = 18 (в.) – купейні вагони.

2) 18 – 12 = 6 (в.)

Відповідь: у потязі 6 плацкартних вагонів.

Щоб знайти число за значенням його дробу, потрібно дане число поділити на чисельник дробу і одержаний результат помножити на його знаменник.

 

Завдання 637

Відстань від Чернівців до Києва 560 км, що становить 4/5 відстані від Чернівців до Чернігова через Київ. Яка відстань між Чернівцями і Черніговом через Київ? Яка відстань від Києва до Чернігова? Доповни схему. Спробуй розв’язати задачу різними способами.

Розв’язання

1-й спосіб

1) 560 : 4 • 5 = 700 (км) – від Чернівців до Чернігова

2) 700 – 560 = 140 (км) – від Києва до Чернігова

2-й спосіб

1) 560 : 4 = 140 (км) – відстань від Києва до Чернігова.

2) 140 + 560 = 700 (км) – відстань від Чернівців до Чернігова.

Відповідь: між Чернівцями і Черніговом 700 км, а від Києва до Чернігова 140 км.

 

Завдання 638

20 дм • 5 = 100 дм 20 дм : 5 = 4 дм З дм 4 см : 17 = 34 см : 17 = 2 см 5 см 6 мм : 8 = 56 мм : 8 = 7 мм	15 т : З = 5 т 15 т 3 ц : З = 5 т 1 ц 15 т 5 ц : 5 = 3 т 1 ц З ц 50 кг : 7 = 350 кг : 7 = 50 кг
12 год : 2 = 6 год 1 год : 2 = 60 хв : 2 = 30 хв 5 год : 2 = 300 хв : 2 = 150 хв = 2 год 30 хв 5 год 40 хв : 17 = 340 хв : 17 = 20 хв

Завдання 639

Учні й учениці четвертого класу зібрали для класної бібліотеки 96 книжок. Література про тварин становила 1/6, пригодницькі книжки — 2/6 усіх книжок, книги про фантастичні події — 1/4 залишку, а решта — казки. Скільки книжок кожної тематики зібрали діти?

^{Короткий запис}

^{Усіх — 96 кн.}

^{Про тварин — 1/6 усіх кн.}

^{Пригодницькі — 2/6 усіх кн.}

^{Фантастичні — 1/4 залишку}

^{Казки — решта}
Розв'язання

1) 96 : 6 = 16 (кн.) – книжки про тварин

2) 96 : 6 • 2 = 32 (кн.) – пригодницькі книжки

3) 16 + 32 = 48 (кн.) – пригодницькі і книжки про тварин разом

4) 96 – 48 = 48 (кн.) – залишок

5) 48 : 4 = 12 (кн.) – книги про фантастичні події

6) 96 – (48 + 12) = 36 (кн.) – казки

Відповідь: діти зібрали 16 книжок про тварин, 32 пригодницькі книжки, 12 книжок про фантастичні події, 36 казок.

 

Завдання 641

Господиня засіяла морквою 20 м² землі, що становить 1/12 всієї площі земельної ділянки, відведеної під городні культури. Площа під городніми культурами становить 1/5 площі дачної ділянки. Чому дорівнює площа подвір’я, якщо вона становить 3/24 площі всієї дачної ділянки?

Розв'язання

1) 20 • 12 = 240 (м²) – площа під городніми культурами

2) 240 • 5 = 1200 (м²) – площа дачної ділянки

3) 1200 : 24 • 3 = 150 (м²) – площа подвір'я

Відповідь: площа подвір'я 150 м².

 

Завдання 642

1) Від туристичної бази одночасно в протилежних напрямах вийшли 2 лижники. Швидкість одного з них 10 км/год, а швидкість іншого — становила 4/5 швидкості першого. Якою буде відстань між ними через 3 год?

Завдання 643

Периметр рівностороннього трикутника 12 см, що становить 6/10 периметра квадрата. На скільки сантиметрів сторона квадрата довша від сторони трикутника?

Завдання 644

а) Ціна порції морозива зменшилася на 6 грн. Це становить 3/10  попередньої ціни. Якою була ціна морозива?

Відповідь: ціна морозива 20 грн.

б) Ми пройшли 900 м. Це становить 9/20 запланованого шляху. Скільки метрів нам доведеться ще йти?

Відповідь: ще доведеться йти на 1100 метрів.

 

Завдання 645 Знайди число за значенням його дробу, якщо

а) 2/5 числа становить 30; 30 : 2 • 5 = 15 • 5 = 75

б) 5/100 числа — це 200. 200 : 5 • 100 = 40 • 100 = 4000

 

Завдання 646

Швидкість польоту бджіл без нектару приблизно 60 км/год, а з нектаром — 18 км/год. Яку відстань долає бджола за 45 хв польоту з нектаром і без нього? Визнач швидкість руху бджоли в метрах за хвилину.

 

Завдання 647

Бджола може зависнути в повітрі. Для цього вона робить 250 помахів крилами за 1 с. Скільки помахів крилами бджола зробить за 7 с висіння в повітрі?

^{Короткий запис}

^{1 с. — 250 п.}

^{7 с. — ?}

Розв'язання 

х 250

    7

 1750 (п.)

Відповідь: бджола робить 1750 помахів крилами.

 

Завдання 648

Побудуй за зразком.

а) 1) Поділи циркулем коло на 6 рівних частин.

2) З’єднай кожну другу точку на колі. Яка фігура утворилася? Шестикутник

б) 1) Проведи 2 будь-які діаметри кола.

2) З’єднай точки на колі попарно. Яка фігура утворилася? Трикутник

Скільки радіусів і діаметрів можна провести в колі? У крузі? Безліч

Які завдовжки радіуси одного кола, круга? r А діаметри? r • 2

Інші завдання дивись тут...