ГДЗ Істер 5 клас математика завдання 76 – 113 до підручника ВІДПОВІДІ

Числові та буквенні вирази. Рівняння

Завдання 76 Вирази

Числові вирази	Буквенні виоази
1) (7 + 14) – 2 = 21 – 2 = 19 4) 25 + 36 : 9 = 25 + 4 = 29 5) 7 • 3 – 5 • 0 = 21 – 0 = 21	2) (a + b) : 7 3) c – 2 + m 6) р • (2 – а)

Завдання 77 Обчисли значення виразу та дізнаєшся рік заснування міста Кременець Тернопільської області.

3150 – (980 : 28 + 17) • 37 = 1226 (рік)
_980 \| 28 84 35 _140 140 0	+ 35 17 52	х 52 37 364 156 1924	_ 3150 1924 1226

Завдання 78 Знайди значення виразу та пригадаєш рік здобуття незалежности Україною.

2073 – (27 • 82 + 164) : 29 = 1991 (рік)
х 27 82 54 216 2214	+ 2214 164 2378	_2378 \| 29 232 82 _58 58 0	_ 2073 82 1991

Завдання 79

Якщо а = 17, то 1258 : а + 374 = = 1258 : 17 + 374 = 448			Якщо а = 37, то 1258 : а + 374 = = 1258 : 37 + 374 = 408
_1258 \| 17 119 74 _68 68 0	+ 74 374 448	+ 74 374 448	_1258 \| 37 111 34 _148 148 0	+ 34 374 408

Завдання 80

Якщо а = 18186, b = 3879, то b + а : 7 – 1599 = = 3879 + 18186 : 7 – 1599 = 4878
_18186 \| 7 14 2598 _41 35 _68 63 _56 56 0	+ 3879 2598 6477	_ 6477 1599 4878

Завдання 81

Якщо х = 12389, у = 463, то х – 15 • y + 17987 = = 12389 – 15 • 463 + 17987 = 23431
х 463 15 2315 463 6945	_ 12389 6945 5444	+ 5444 17987 23431

Завдання 82 Правила знаходження невідомих компонентів

1) Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.

2) Щоб знайти від’ємник, треба від зменшуваного відняти різницю.

3) Щоб знайти зменшуване, треба до різниці додати від’ємник.

4) Щоб знайти невідомий множник, треба добуток поділити на відомий множник.

5) Щоб знайти ділене, треба частку помножити на дільник.

6) Щоб знайти дільник, треба ділене поділити на частку.

Завдання 83 Рівняння

х + 2971 = 5317 x = 5317 – 2971 x = 2346	12492 – х = 7543 x = 12492 – 7543 х = 4949	х – 72581 = 2143 x = 72581 + 2143 x = 74724	12371 + х = 19002 x = 19002 – 12371 x = 6631
_ 5317 2971 2346	_ 12492 7543 4949	+ 72581 2143 74724	_ 19002 12371 6631

Завдання 84

35492 – х = 9871 x = 35492 – 9871 x = 25 621	х + 2387 = 4005 x = 4005 – 2387 x = 1618	х – 4589 = 987 x = 4589 + 987 x = 5576	13892 + х = 79159 x = 79159 – 13892 x = 65 267
_ 35492 9871 25621	_ 4005 2387 1618	+ 4589 987 5576	_ 79159 13892 65267

Завдання 85

х • 24 = 15 048 x = 15 048 : 24 x = 627	х : 427 = 25 x = 427 • 25 x = 10675	29 008 : х = 37 x = 29 008 : 37 x = 784
_15048 \| 24 144 627 _64 48 _168 168 0	х 427 25 2135 854 10675	_29008 \| 37 259 784 _310 296 _148 148 0

Завдання 86

6426 : х = 42 x = 6426 : 42 x = 153	х : 38 = 529 x = 38 • 529 x = 20102	56 • х = 48 552 x = 48 552 : 56 x = 867
_6426 \| 42 42 153 _222 210 _126 126 0	х 529 38 4232 1587 20102	_48552 \| 56 448 867 _375 336 _392 392 0

Завдання 87 Запиши вираз та знайди його значення:

1) від числа 11 209 відняти добуток 45 і 203; 11 209 – 45 • 203 = 2074	х 203 45 1015 812 9135	_11209 9135 2074
2) до числа 1239 додати частку 6084 і 39. 1239 + 6084 : 39 = 1395	_6084 \| 39 39 156 _218 195 _234 234 0	+1239 156 1395

Завдання 88 Запиши вираз та знайди його значення:

від добутку чисел 307 і 48 відняти частку чисел 14 007 і 69.

307 • 48 – 14 007 : 69 = 14533
х 307 48 2456 1228 14736	_14007 \| 69 138 203 _207 207 0	_ 14736 203 14533

Завдання 89

У північній півкулі карти зоряного неба звіздар нарахував 5425 зірок, а у південній півкулі — на m зірок менше.

1) Вираз: 5425 – m (з.) – кількість зірок у південній півкулі зоряного неба;

2) вираз: 5425 + (5425 – m) (з.) – кількість зірок в обох півкулях зоряного неба.

3) Якщо m = 198, то

5425 – 198 = 5227 (з.)

5425 + (5425 – 198) = 5425 + 5227 = 10 652 (з.)

Відповідь: у південній півкулі 5227 зірок, а в двох півкулях разом 10652 зірки.

Завдання 90

Остап з Орисею наліпили з капустою n вареників, а з м’ясом — на 12 вареників більше.

1) Вираз: n + 12 (в.) – кількість з м’ясом;

2) Вираз: n + (n + 12) (в.) – загальна кількість, які наліпили друзі;

3) Якщо n = 17, то

17 + 12 = 29 (в.)

17 + (17 + 12) = 46 (в.)

Відповідь: з м'ясом 29 вареників, а всього наліпили 46 вареників.

Завдання 91 Рівняння

х + 2726 : 47 = 207

x + 58 = 207

x = 207 – 58

x = 149

_2726 | 47

235 58

_376

376

_ 207

149

х : 42 = 213 + 405

x : 42 = 618

x = 618 • 42

x = 25956

+213

405

618

х 618

1236

2472

25956

Завдання 92 Рівняння

42 • 54 + х = 3041

2268 + x = 3041

x = 3041 – 2268

x = 773

× 42

168

210

2268

_3041

2268

773

х – 432 = 3510 : 78

x – 432 = 45

x = 432 + 45

x = 477

_3510 | 78

312 45

_390

390

+432

477

Завдання 93, 94

Знайди таке значення а, щоб число 7 було розв’язком

а – х • 3 = 9

За умовою x = 7, тому

a – 7 • 3 = 9

a – 21 = 9

a = 30

Відповідь: а = 30

Перевірка: 30 – 7 • 3 = 9

Знайди таке значення b, щоб число 6 було розв’язком

30 : х + b =12

За умовою x = 6, тому

30 : 6 + b = 12

5 + b = 12

b = 12 – 5

b = 7

Відповідь: а = 7

Перевірка: 30 : 6 + 7 = 12

Геометричні фігури на площині

Завдання 95

Фігури: відрізок, точка, коло, квадрат, промінь, кут або ламана, прямокутник, пряма, шестикутник, трикутник, ламана, круг.

Завдання 96

Виміряй відрізки АВ і СВ та порівняй їх довжини.

АВ = 4 см, СВ = 4 см 5 мм.

Оскільки 4 см < 4 см 5 мм, тому AB < CB.

Завдання 97

Побудуй відрізок КL, довжина якого 47 мм.

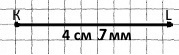
Завдання 98

Визнач «на око» вид кожного кута: гострий, прямий, тупий, гострий, гострий

Перевір за допомогою косинця. Виконай відповідні записи.

Завдання 99

Накресли гострий кут АОВ. Проведи промінь ОК так, щоб кут КОВ був тупим.

Завдання 100 Накресли тупий кут СОВ. Проведи промінь ОМ так, щоб кути СОМ і МОВ були гострими.

Завдання 101 Знайди периметр і площу

1) квадрата зі стороною 5 см;

5 • 4 = 20 (см) – периметр квадрата.

5 • 5 = 25 (см²) – площа квадрата.

2) прямокутника зі сторонами 3 см і 8 см.

(3 + 8) • 2 = 11 • 2 = 22 (см) – периметр прямокутника.

3 • 8 = 24 (см²) – площа прямокутника.

Геометричні фігури на площині

Завдання 102

Площа прямокутника 24 см², а його довжина 6 см. Побудуй цей прямокутник.

24 : 6 = 4 (см) – ширина прямокутника.

Завдання 103

Ширина прямокутника дорівнює 3 см, а його площа — 15 см². Побудуй цей прямокутник.

15 : 3 = 5 см – довжина прямокутника.

Завдання 104

1) Побудуй коло із центром у точці О, радіус якого 25 мм.

2) Проведи діаметр кола СВ та виміряй його довжину у міліметрах. СВ = 50 мм

3) Чи можна стверджувати, що радіус кола удвічі менший за діаметр?

Можна, бо 50 мм : 25 мм = 2

Завдання 105

1) Знайди радіус кола, діаметр якого дорівнює 4 см.

4 : 2 = 2 (см) – радіус кола

2) Побудуй це коло.

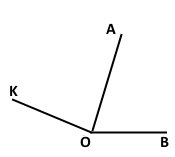
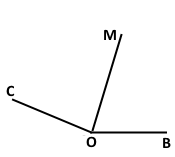
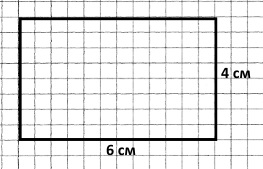
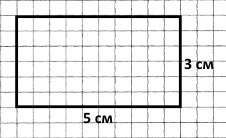
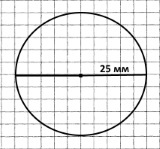
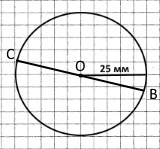
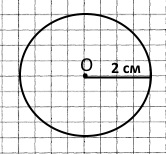
Завдання 106

Знайди периметр п’ятикутника, у якого три сторони по 5 см і дві сторони — по 7 см.

P = 5 • 3 + 7 • 2 = 15 + 14 = 29 (см)

Завдання 107

Знайди периметр шестикутника, у якого чотири сторони по 6 см, а дві — по 8 см.

P = 6 • 4 + 8 • 2 = 24 + 16 = 40 (см)

Завдання 108

Методом підбору знайди сторону квадрата, площа якого дорівнює 9 см²; 36 дм²; 4 м².

формула: S = а • а
9 см² = 3 см • 3 см Відповідь: 3 см.	36 дм² = 6 дм • 6 дм Відповідь: 6 дм.	4 м² = 2 м • 2 м Відповідь: 2 м.