Інші завдання дивись тут... 

Завдання 470

а) 1 —  найменший дільник числа 24;

б) 24 — найбільший дільник числа 24;

в) 2 — найменший простий дільник числа 24.

 

Завдання 471

Так, число 5 спільним дільником чисел 100 і 125.

НСД(100, 125) = 25

 

Завдання 472

Взаємно простими із числом 6 є кілька чисел: 5, 7 і 11,

бо НСД(6;5) = 1, НСД(6;7) = 1, НСД(6;11) = 1

 

Завдання 473

Чи можуть бути взаємно простими будь-які два числа, записані парними цифрами? Ні, бо тоді їхній найбільший спільний дільник не буде дорівнювати 1.

 

Завдання 476

1 — В; 2 — А; 3 — Б

 

Завдання 477 Ознаки подільності чисел

Відомо, що НСД (12, n) = 6. Чи ділиться число:
на 2: так	на 3: так	на 4: ні	на 6: так	на 12: ні

Завдання 478

Яку найбільшу кількість однакових подарунків можна зробити з 12 наліпок і 18 обкладинок?

Розв'язання

НСД(12, 18) = 2 • 3 = 6

Відповідь: А 6.

 

Завдання 479

Яку найбільшу кількість однакових букетів можна скласти з 15 нарцисів і 18 тюльпанів?

Розв'язання

НСД(15, 18) = 3

Відповідь: 3 букети.

 

Завдання 480 Спільні дільники чисел: 

Дано розклади чисел на множники: a = 2 • 2 • 11, b = 2 • 2 • 2 • 7, c = 2 • 2 • 2 • 3 • 5. 

а) НСД (a;b) = 2 • 2 = 4

б) НСД (a;c) = 2 • 2 = 4

в) НСД (b;c) = 2 • 2 • 2 = 8

 

Завдання 485

Дано розклади чисел на множники: x = 2³ • 5², y = 2² • 3 • 5², z = 2 • 3² • 5³. 

а) НСД (x;y) = 2 • 2 • 5 • 5 = 100

б) НСД (x;z) = 2 • 5 • 5 = 50 

в) НСД (y;z) = 2 • 3 • 5 • 5 = 150

 

Завдання 486

Чи правильно, що числа 23 і 45 взаємно прості? А числа 23 і 46? Відповідь обґрунтуй.

Числа 23 і 45 є взаємно простими, бо НСД(23;45) = 1.

Числа 23 і 46 не є взаємно простими, бо НСД(23;46) = 23.

 

Завдання 487

з даних пар чисел взаємно прості:
а) 16 і 9; Так	б) 18 і 81; Ні	в) 11 і 121. Ні

Завдання 488

Чи взаємно прості числа 1002 і 2001? А числа 1001 і 1010?

Числа 1002 і 2001 не є взаємно простими, бо НСД(1002, 2001) = 3

Числа 1001 і 1010 є взаємно простими, бо НСД(1001, 1010) = 1

 

Завдання 489

а) числа 375 і 896 є взаємно простими, бо НСД(375, 896) = 1;

б) числа 2025 і 968 є взаємно простими, бо НСД(2025, 968) = 1;

в) числа 1225 і 2888 є взаємно простими, бо НСД(1225, 2888) = 1.

 

Завдання 490

а) числа 1521 і 1408 є взаємно простими, бо НСД(1521, 1408) = 1;

б) числа 648 і 578 не є взаємно простими, бо НСД(648, 578) = 2;

в) числа 1512 і 275 є взаємно простими, бо НСД(1512, 275) = 1.

 

Завдання 491

Яка найбільша кількість однакових подарунків могла бути на святі, якщо у всіх них разом було 106 книжок і 159 браслетів. Скільки книжок і скільки браслетів було в кожному подарунку?

Розв'язання

1) НСД(106;159) = 53 (п.) ‒ найбільша кількість однакових подарунків;

2) 106 : 53 = 2 (кн.) ‒ книжок в кожному подарунку;

3) 159 : 53 = 3 (бр.) ‒ браслетів в кожному подарунку.

Відповідь: 53 подарунки, у кожному 2 книги і 3 браслети.

 

Завдання 492

Усі команди в «Математичних боях» складалися з однакової кількості хлопців і дівчат. Яка найбільша кількість команд могла бути, якщо всього було 85 хлопців і 102 дівчини. Скільки дівчат і скільки хлопців було в кожній команді?

Розв'язання

НСД(85;102) = 17 ‒ найбільша кількість команд;

85 : 17 = 5 (д.) ‒ хлопців в кожній команді;

102 : 17 = 6 (д.) ‒ дівчат в кожній команді.

Відповідь: 17 команд, у кожній 5 хлопців і 6 дівчат.

 

Завдання 493

Аркуш паперу, довжина якого дорівнює 35 см, а ширина — 21 см, розрізали на найбільші з усіх можливих рівні квадрати. Скільки отримали квадратів?

НСД(35, 21) = 7, отже квадрат має сторону 7, тому їх 15.

 

Завдання 494

Довжина басейну 10,5 м, а ширина  — 7,5 м. Дно басейну  потрібно викласти однаковими плитками, що мають форму квадрата. Яку найбільшу довжину може мати сторона плитки, щоб її не потрібно було різати? Скільки потрібно таких плиток?

Розв'язання

10,5 м = 105 дм, 7,5 м = 75 дм

1) НСД(105, 75) = 15 (дм) = 1,5 (м) ‒ сторона плитки;

2) (105 • 75) : (15 • 15) = 7875 : 225 = 35 (пл.) ‒ стільки потрібно плиток.

Відповідь: 1,5 м і 35 плиток.

 

Завдання 495, 496

Число a ділиться на n. Чи можуть ці числа бути взаємно простими? Ні, числа a та n не можуть бути взаємно простими, оскільки вони мають спільний дільник n, і тому їхній найбільший спільний дільник (НСД) не може бути рівним 1.

 

Завдання  498

Число a ділиться на просте число p. Чи можуть ці числа бути взаємно простими? Ні, числа a та просте число p не можуть бути взаємно простими, оскільки вони мають спільний дільник p, і тому їхній найбільший спільний дільник (НСД) не може бути рівним 1.

 

Завдання 499

Наведіть приклади чисел a, b, c таких, що НСД (a, b) = 2, НСД (a, c) = 3, НСД (b, c) = 5.

a = 12, b = 10, c = 15

 

Завдання 500

Числа a, b, c такі, що НСД (a, b) = 2, НСД (b, c) = 3. Знайди НСД (a, b, c). 

a = 4, b = 6, c = 3; НСД (4, 6, 3) = 1

 

Завдання 501

У таборі дітям роздали порівну 96 бандан і 160 футболок. Скільки дітей є в таборі, якщо їх від 10 до 30? Скільки футболок і бандан отримає кожна дитина?

Розв'язання

НСД(96, 160) = 32, оскільки дітей від 10 до 30, тому в таборі 16 дітей.

96 : 16 = б (б.) ‒ роздали бандан;

160 : 16 = 10 (ф.) ‒ роздали футболок.

Відповідь: 16 дітей; 6 банданів і 10 футболок.

 

Завдання 502

Місто закупило 105 лавочок і 140 смітників і має розподілити їх порівну по парках. Скільки парків у місті, якщо їх більше 5, але менше 15. Скільки лавочок та смітників розмістять в кожному парку?

Розв'язання

НСД(105, 140) = 35 = 5 • 7, отже у місті 7 парків і закупило по 15 лавочок і 20 смітників.

Відповідь: 15 лавочок і 20 смітників.

 

Завдання 503

Доведи, що числа 9, 10 і a взаємно прості, яким би не було натуральне число a.

Для того щоб довести, що числа 9, 10 та будь–яке натуральне число a є взаємно простими, треба переконатися, що їхній найбільший спільний дільник (НСД) дорівнює 1.

Розглянемо всі можливі випадки для натурального числа a:

1. Якщо a = 1: Найбільший спільний дільник чисел 9, 10 і 1 дорівнює 1, оскільки 9 та 10 прості між собою.

2. Якщо a є простим числом: Якщо a є простим числом, то воно не має спільних простих множників з числами 9 та 10, оскільки 9 та 10 не прості числа. Отже, їхній НСД також буде 1.

3. Якщо a є складним числом: Якщо a є складним числом, то його розкладаємо на прості множники. Оскільки 9 і 10 взаємно прості і не мають спільних простих множників, то будь–який спільний дільник між ними та числом a також буде мати тільки спільні прості множники з 1. Таким чином, НСД буде 1.

Отже, незалежно від значення натурального числа a, числа 9, 10 та a є взаємно простими, і їхній найбільший спільний дільник завжди дорівнює 1.

 

Завдання 504

Доведи, що при будь–яких натуральних значеннях a і b числа 15, 22, a і b взаємно прості.

Оскільки 15 і 22 взаємно прості і не мають спільних простих множників, то будь–який спільний дільник між ними та числами a і b також буде мати тільки спільні прості множники з 1. Таким чином, НСД буде 1.

Отже, незалежно від значення натуральних чисел a і b, числа 15, 22, a та b є взаємно простими, і їхній найбільший спільний дільник завжди дорівнює 1.

 

Скільки існує різних трицифрових чисел, записаних різними цифрами 4, 6 і 8? Знайдіть НСД усіх цих чисел.

Існує 6 таких чисел: 468, 486, 648, 684, 846, 864.

Завдання 506

Кількість учнів / учениць, які навчаються в 6 класах, більша за 90, але менша, ніж 100. Третина цих учнів / учениць займаються спортом, четверта частина — музикою, а решта — танцями. Скільки учнів / учениць займаються танцями?

Нехай у класах x дітей, тоді займаються спортом 1/3 x, а музикою — 1/4 x.

Отже, займаються танцями: x − (1/3 x + 1/4 x) = 5/12 x

Враховуючи умову 90 < x < 100: 5/12 x = 5/12 • 96 = 40 (д.) ‒ займаються танцями.

 

Завдання 507

Чи може бути в лютому п’ять понеділків? Так, якщо це високосний рік, коли лютий має 29 днів, і 1 число місяця це понеділок.

 

Завдання 508

На малюнку 27 трикутників.

 

Вправи для повторення

Завдання 509

У скільки разів сума чисел 894 і –892 менша за їх різницю?

Розв'язання

894 + (–892) = 2

894 ‒ (–892) = 894 + 892 = 1786

1786 : 2 = 893

Відповідьь: у 893 разів менша.

 

Завдання 510

Поїзд їде зі швидкістю 60 км/год. Скільки кілометрів він проїде за 2,5 год? За скільки хвилин він проїде 0,5 км?

Розв'язання

1) 60 • 2,5 = 150 (км) ‒ проїде відстань за 2,5 год;

2) 60 • 0,5 = 30 (хв) ‒ за стільки хвилин поїзд проїде 0,5 км.

Відповідь: 150 км і 30 хв.

 

Завдання 511

Накресли дві прямі, які перетинаються під кутом 60. Знайди міри трьох інших кутів, утворених цими прямими.

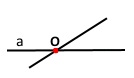
Кут, що лежить навпроти кута 60° теж дорівнює 60°. Інші два кути рівні:

(360° ‒ 60° ‒ 60°) : 2 = 120°

Відповідь: 60°; 120°; 120°.

Інші завдання дивись тут...