© ГДЗ 8next.com, 2013, 2018, 2022
Запитання
1. Яка фігура обмежує многокутник? Многокутник обмежує замкнена ламана, що складається з декількох ланок.
3. Які елементи многокутника ви знаєте? Сторони, вершини.
3. Що називають периметром многокутника? Периметр многокутника ‒ сума довжин усіх сторін многокутника.
4. Які фігури називають рівними? Дві фігури називають рівними, якщо вони суміщаються при накладанні.
Розв’язуємо усно
Завдання 1 Суму чисел 24 і 18 зменшити на 33.
(24 + 18) ‒ 33 = 42 ‒ 33 = 9
Завдання 2 Різницю чисел З0 і 14 збільште у 3 рази.
(30 ‒ 14) • 3 = 16 • 3 = (10 + 6) • 3 = 30 + 18 = 48
Завдання 3 Добуток чисел 12 и 5 збільште на 19.
(12 • 5) + 19 = 60 + 19 = 79
Завдання 4 Частку чисел 189 и 9 зменшіть у 7 разів.
(189 : 9) : 7 = 21 : 7 = 3
Завдання 5 Укажіть серед даних відрізків рівні, якщо
АВ = 5 см 3 мм, CD = 4 м 5 см, РК = 45 см, EF = 2 дм 8 мм, TQ = 53 мм, MN = 208 мм.
АВ = TQ, MN = EF
Вправи
Вправа 349° Назвіть вершини і сторони п’ятикутника, зображеного на рисунку 121.
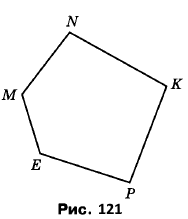
Вершини E, M, N, K, P
Сторони EM, MN, NK, KP, PE
Вправа 350° Нарисуйте: 1) чотирикутник; 2) п’ятикутник; 3) шестикутник; 4) семикутник.
Вправа 351° Обчисліть периметр п’ятикутника, сторони якого дорівнюють 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.
Розв'язання
Р = 2 см + 4 см + 5 см + 5 см 5 мм + 6 см + 7 см = (2 см + 4 см + 5 см +
+ 6 см + 7 см) + 5 мм = 24 см 5 мм ‒ периметр п’ятикутника.
Вправа 352 Обчисліть периметр шестикутника, три сторони якого дорівнюють по 8 см, а три інші — по 10 см.
Розв'язання
Р = 8 см • 3 + 10 см • 3 = 24 см + 30 см = 54 см
Вправа 353° Нарисуйте в зошиті фігуру, яка рівна тій, що зображена на рисунку 122.
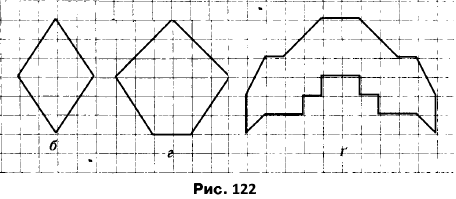
Вправа 354 Нарисуйте в зошиті фігуру, яка рівна тій, що зображена на рисунку 123.
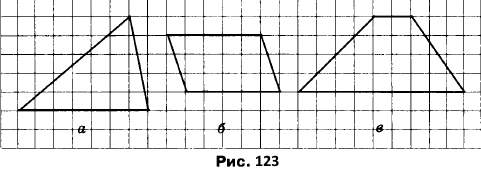
Вправа 355 Одна із сторін чотирикутника дорівнює 8 см, друга сторона у 3 рази більша за першу, а третя — на 7 см менша від другої і на 9 см більша за четверту. Обчисліть периметр чотирикутника.
Короткий запис
I — 8 см
II — ?, у 3 рази більша, ніж I
III — ?, на 7 см менша від II і на 9 см більша від IV
IV — ?
Периметр — ?
Розв'язання
1) 8 • 3 = 24 (см) ‒ довжина другої сторони.
2) 24 ‒ 7 = 17 (см) ‒ довжина третьої сторони.
3) 17 ‒ 9 = 8 (см) ‒ довжина четвертої сторони.
4) 8 + 24 + 17 + 8 = 57 (см)
Відповідь: периметр чотирикутника 57 см.
Вправа 356 Сторони п’ятикутника пронумерували. Перша сторона дорівнює 4 см, а кожна наступна сторона на 2 см довша за попередню. Обчисліть периметр п’ятикутника.
Короткий запис
I — 4 см
II — ?, на 2 см більша від I
III — ?, на 2 см більша від II
IV — ?, на 2 см більша від III
V — ?, на 2 см більша від IV
Периметр — ?
Розв'язання
1) 4 + 2 = 6 (см) ‒ довжина другої сторони.
2) 6 + 2 = 8 (см) ‒ довжина третьої сторони.
3) 8 + 2 = 10 (см) ‒ довжина четвертої сторони.
4) 10 + 2 = 12 (см) ‒ довжина п'ятої сторони.
5) 4 + 6 + 8 + 10 + 12 = 40 (см)
Відповідь: периметр п’ятикутника дорівнює 40 см.
Вправа 357
1) Скільки діагоналей можна провести з однієї вершини: а) п’ятикутника; б) дев’ятикутника; в) n‒кутника, де n > З?
а) 5 ‒ 3 = 2 діагоналі; б) 9 ‒ 3 = 6 діагоналей; в) n ‒ 3 діагоналей.
2) Скільки всього діагоналей можна провести: а) у п’ятикутнику; б) у дев’ятикутнику; в) у n‒кутнику, де п > З?
а) 5 • (5 ‒ 3) : 2 = 5 діагоналей,
б) 9 • (9 ‒ 3) : 2 = 27 діагоналей;
в) n • (n ‒ 3) : 2 діагоналей.
Вправи для повторення
Вправа 358 Одиниці вимірювання
|
1) 3986 г < 4 кг, бо 4 кг = 4000 г 2) 6 м < 712 см, бо 6 м = 600 см |
3) 60 см < 602 мм, бо 69 см = 600 м 4) 999 кг < 10 ц, бо 10 ц = 1000 кг |
Вправа 359 Виконайте додавання, обираючи зручний порядок обчислення:
1) (636 + 927) + 364 = (636 + 364) + 927 = 1000 + 927 = 1927
2) (425 + 798) + 675 = (425 + 675) + 798 = 1100 + 798 = 1898
3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1000 + 1300 = 2300
4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1000 + 1400 = 2400
Вправа 360 Відомо, що <ABC = 74°, а промінь BD — його бісектриса. Обчисліть величину кута DBC.
Розв'язання
Оскільки бісектриса дітить будь-який кут навпіл, то
<DBC = <ABC : 2 = 74° : 2 = 37°
Вправа 361 Найвища вершина Кримських гір — гора Роман‒Кош має висоту 1545 м. Вона на 477 м нижча від карпатської гори Піп‒Іван Чорногорський, яка на 86 м вища за гору Піп‒Іван Мармароський. Яка висота найвищої гори України Говерли, якщо вона на 125 м вища за гору Піп‒Іван Мармароський?
Розв'язання
1) 1545 + 477 = 2022 (м) ‒ висота Піп‒Іван Чорногорський.
2) 2022 ‒ 86 = 1936 (м) ‒ висота гори Піп‒Іван Мармароський.
3) 1936 + 125 = 2061 (м)
Відповідь: висота Говерли 2061 м.
Задача від Мудрої Сови
Вправа 362 Чи існує многокутник, периметр якого дорівнює 1 000 000 см і який можна помістити у квадрат із стороною 1 см? Так, такий многокутник повинен мати багато сторін довжинами, наприклад, до 1 см.
Вправа 363 Лимони однакової маси продають поштучно. Маса кожного лимона, виражена в грамах, є натуральним числом. Купили більше 2, але менше 7 лимонів. Маса всієї покупки становить 850 г. Яка маса одного лимона?
Розв'язання
Можна було б купити 3, 4, 5 або 6 лимонів. Без остачі число 850 г ділиться тільки на 5, тому купили 5 лимонів.
850 : 5 = 170 (г) ‒ маса лимона.
Відповідь: маса лимона 170 г.
------------------------------- у підручнику за 2013, 2018 роки --------------------------
Запитання
2. Чи можуть ланки ламаної, яка обмежує многокутник, перетинатися? Так.
4. Як називають і позначають многокутник? Многокутник називають і позначають за його вершинами, для цього слід послідовно записати або назвати всі його вершини, починаючи з будь‒якої.
6. Які многокутники називають рівними? Многокутники називають рівними , якщо вони суміщаються при накладанні.
8. Що називають діагоналлю многокутника? Діагоналлю многокутника називають відрізок, який сполучає дві несусідні його вершини.
Вправа 334* Як, використовуючи шаблон кута, градусна міра якого дорівнює 13°, побудувати кут, градусна міра якого дорівнює 2°?
Розв'язання
(13° • 14) ‒ 180° = 182° ‒ 180° = 2°
Вправа 335* Як побудувати кут, градусна міра якого 1°, використовуючи шаблон кута, градусна міра якого дорівнює: 1) 19°; 2) 7°?
Розв'язання
1) (19° • 19) ‒ 180° • 2 = 361° ‒ 360° = 1°
2) (7° • 13) ‒ 90° = 91° ‒ 90° = 1°