Теорема – математичне твердження, яке потребує доведення

Інші завдання дивись тут...

ТЕОРЕМА — математичне твердження, справедливість якого встановлюється за допомогою міркування, яке називають доведенням теореми.

Доводячи теорему, можна користуватися аксіомами, а також раніше доведеними теоремами.

^{Зауважимо, що жодні інші властивості геометричних фігур (навіть якщо вони здаються нам очевидними) використовувати не можна.}

Будова теореми

Має умову (те, що дано), доведення із висновком (те, що потрібно довести).

ПЕРЕЛІК ТЕОРЕМ

◊ Теорема Піфагора.

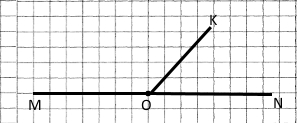
◊ Теорема (властивість суміжних кутів).

Сума суміжних кутів дорівнює 180°.

Доведення. Нехай кути MOK і KON суміжні кути, тоді промені ОМ і ОN є доповняльними. За основною властивістю вимірювання кутів ∠MOK + ∠KON = ∠MON. Кут MON, утворений доповняльними променями, є розгорнутим, тобто ∠MOK + ∠KON = 180°. Теорему доведено.

Наслідок 1. Кут, суміжний з прямим кутом, — прямий.

Наслідок 2. Кут, суміжний з гострим кутом, — тупий; кут, суміжний з тупим кутом, — гострий.

Наслідок 3. Кути, суміжні до рівних кутів, є рівними.

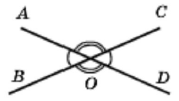
◊ Теорема (властивість вертикальних кутів).

Вертикальні кути рівні між собою.

Доведення. Нехай кути AOB і COD – вертикальні. Оскільки кути AOB і AOC суміжні, то ∠AOB + ∠AOC = 180°. Також суміжні кути AOC і COD, тому ∠AOC + ∠COD = 180°. Маємо: ∠AOC = 180° – ∠AOB і ∠AOC = 180° – ∠COD. Праві частини цих рівностей рівні, тому рівними є і ліві їхні частини. Отже, ∠AOB = ∠COD. Теорему доведено.

◊ Теорема.

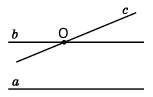
Якщо пряма перетинає одну з двох паралельних прямих, то вона перетинає і другу.

Доведення (від супротивного). Нехай а і b – паралельні прямі і пряма с перетинає пряму в точці О. Припустимо, що пряма с не перетинає пряму а, тобто с ǁ а. Тоді через точку О проходять дві прямі b і с, які обидві паралельні прямій а. Це суперечить аксіомі паралельності прямих. Отже наше припущення хибне, правильним є те, що пряма с перетинає пряму а. Твердження доведено.

◊ Теорема.

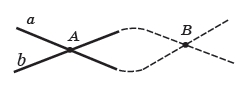
Будь-які дві прямі, що перетинаються, мають тільки одну спільну точку.

Доведення. Нехай прямі а і b, що перетинаються, крім спільної точки А, мають ще одну спільну точку В. Тоді через дві точки проходять дві прямі. А це суперечить основній властивості прямої. Отже наше припущення про наявність другої точки перетину прямих а і b неправильне.

◊ Теорема (ознака паралельності прямих).

Якщо при перетині двох прямих січною відповідні кути рівні, то прямі паралельні.

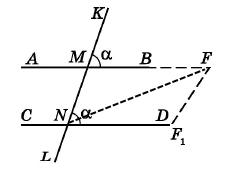
Нехай при перетині прямих AB і CD січною KL утворилися рівні між собою відповідні кути ∠KMB = ∠MND = α.

Доведення (методом від супротивного).

Припустимо, що дані прямі AB і CD не паралельні, а перетинаються в деякій точці F. Не змінюючи міри кута KMB, перенесемо його так, щоб вершина кута – точка M – збіглася з точкою N, промінь MK збігся з променем NM, а промінь MB зайняв положення променя NF₁. Тоді ∠MNF₁ = ∠KMF = а. Оскільки промінь NF₁ не збігається з променем NF, бо F ₵ NFX, то ∠MNF₁ ≠ ZMNF. Але ж було встановлено, що ∠MNF = α і ∠MNF₁ = α.

Прийшли до протиріччя, бо наше припущення про те, що прямі AB і CD не паралельні, було хибним. А отже, прямі AB і CD паралельні, що й потрібно було довести.

◊ Наслідок 1. Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні між собою, то прямі паралельні.

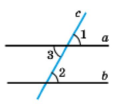
Дано січна с до прямих а і b, внутрішні різносторонні кути рівні, наприклад, ∠3 = ∠2

Доведення. Нехай при перетині прямих a і b січною c внутрішні різносторонні кути виявилися рівними. Але кути 3 і 1 – вертикальні, тому ∠1 = ∠3. Отже, ∠2 = ∠1. Кути 2 і 1 – відповідні, тому за ознакою паралельності прямих маємо а || b.

◊ Наслідок 2. Якщо при перетині двох прямих січною сума внутрішніх односторонніх кутів дорівнює 180°, то прямі паралельні.

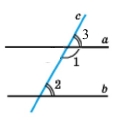
Дано січна с до двох прямих а і b, сума внутрішніх односторонніх кутів ∠1 + ∠2 = 180°.

Доведення. Нехай при перетині прямих a і b січною c сума внутрішніх односторонніх кутів дорівнює 180°, наприклад ∠1 + ∠2 = 180°. Кути 1 і 3 – суміжні, тому ∠1 + ∠3 = 180°.

Із цих двох рівностей випливає, що ∠2 = ∠3. Ці кути є відповідними, а тому прямі a і b – паралельні за ознакою паралельності прямих.

◊ Наслідок 3. Дві прямі, перпендикулярні до третьої прямої, паралельні.

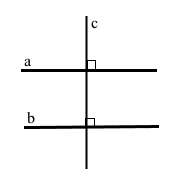
Дано a ﬩ c і b ﬩ с.

Доведення. Кути між прямими a і c, b і c, що перетинаються, дорівнюють 90°. Сума внутрішніх односторонніх кутів дорівнює 180°, враховуючи наслідок 2, маємо a || b.

Зауважимо, що наслідки 1-3 можна також розглядати як ознаки паралельності прямих.

◊ Теорема (властивість паралельних прямих).

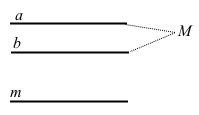
Дві прямі, паралельні третій прямій, паралельні одна одній.

Нехай прямі a і b паралельні прямій с. Доведемо, що a || b.

Застосуємо доведення від супротивного. Припустимо, що прямі a і b не паралельні, а перетинаються в деякій точці M. Отже, через точку M проходять дві прямі a і b, що паралельні прямій m. Це суперечить аксіомі паралельності прямих. Отже, наше припущення є хибним. Тому a || b.

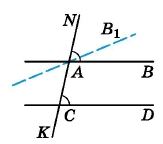
◊ Теорема (властивість відповідних кутів, що утворилися при перетині паралельних прямих січною). Відповідні кути, що утворилися при перетині паралельних прямих січною, рівні між собою.

Нехай паралельні прямі AB і CD перетинає січна NK. Доведемо, що ∠NAB = ∠ACD.

Припустимо, що ∠NAB ≠ ∠ACD. Проведемо пряму AB1 так, щоб виконувалася рівність ∠NAB1 = ∠ACD. За ознакою паралельності прямих прямі AB₁ і CD паралельні. Але ж за умовою і AB || CD. Прийшли до того, що через точку A проходять дві прямі AB і AB1, паралельні прямій CD, що суперечить аксіомі паралельності прямих. Отже, наше припущення є хибним і тому відповідні кути, утворені при перетині паралельних прямих січною, між собою рівні: ∠NAB = ∠ACD.

◊ Наслідок 1 (властивість внутрішніх різносторонніх кутів, утворених при перетині паралельних прямих січною). Внутрішні різносторонні кути, утворені при перетині паралельних прямих січною, рівні між собою.

Нехай паралельні прямі а і b перетинає січна c. Доведемо, що внутрішні різносторонні кути, наприклад 2 і 3, рівні між собою.

Оскільки a || b, то відповідні кути 1 і 2 рівні між собою. Кути 1 і 3 між собою рівні, як вертикальні. З рівностей ∠1 = ∠2 і ∠1 = ∠3 випливає, що ∠2 = ∠3.

◊ Наслідок 2 (властивість внутрішніх односторонніх кутів, утворених при перетині паралельних прямих січною). Сума внутрішніх односторонніх кутів, утворених при перетині паралельних прямих січною, дорівнює 180°.

Нехай паралельні прямі а і b перетинає січна c. Доведемо, що сума внутрішніх односторонніх кутів, наприклад 1 і 2, дорівнює 180°.

Оскільки a || b, то відповідні кути 2 і 3 рівні між собою. Кути 3 і 1 – суміжні, тому ∠3 + ∠1 = 180°, але ж ∠3 = ∠2. Тому ∠2 + ∠1 = 180°.

Інші завдання дивись тут...