Діти з’їли 2/3 пиріжків. Яка частина пиріжків залишилася?
Розвязання
1 − 2/3 = 3/3 − 1/3 = 2/3
Відповідь: залишилася 2/3 частина пиріжків.
Завдання 1039 Додаванння дробів
|
а) 1/5 + 2/5 = 3/5
б) 7/8 – 3/8 = 4/8 = 1/2
в) 2/7 + 2/7 = 4/7
г) 5/9 – 3/9 = 2/9
|
ґ) 1/6 + 5/6 = 6/6 = 1
д) 5/13 + 4/13 = 9/13
е) 2/9 + 7/9 = 9/9 = 1
є) 19/12 – 17/12 = 2/12 = 1/6
|
Завдання 1040 Мішані дроби
|
а) 3 + 4/5 = 3 4/5
б) 2/3 + 5 = 5 2/3
в) 7 + 1/8 = 7 1/8
г) 3/8 + 2 = 2 3/8
|
ґ) 12 + 1/12 = 12 1/12
д) 12/17 + 1 = 1 12/17
е) 5 + 7/7 = 5 7/7 = 6
є) 5/5 + 7 = 7 5/5 = 8
|
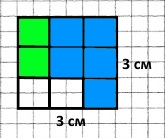
Завдання 1041 Обчисли, користуючись малюнком.
|
а) 1 – 1/8 = 8/8 – 1/8 = 7/8
б) 1 – 3/8 = 8/8 – 3/8 = 5/8
|
в) 1 – 6/8 = 8/8 – 6/8 = 2/8 = 1/4
г) 1 – 7/8 = 8/8 – 1/8 = 1/8
|
Завдання 1042
Оля розв’язала два рівняння і задачу. На перше рівняння вона витратила 1/21 , а на друге — 10/21 часу. Яку частину часу Оля витратила на розв’язування задачі?
Розвязання
1) 1/21 + 10/21 = 11/21 − частину часу витратила на розв'язування двох рівнянь;
2) 1 − 11/21 = 10/21 − частину часу витратила на розв'язування задачі.
Відповідь: В 10/21
Завдання 1043
Назви мішані числа, що відповідають малюнкам: 2 1/3, 1 2/3, 2 1/4
Завдання 1044 Перетворення дробів
|
1 2/5 = 7/5
3 1/3 = 10/3
|
3 1/4 = 13/4
5 3/8 = 43/8
|
6 7/10 = 67/10
10 9/11 = 119/11
|
15 1/4 = 61/4
100 2/3 = 302/3
|
100 5/7 = 705/7
200 2/5 = 1002/5
|
Завдання 1045 Подай у вигляді мішаного числа:
|
3/2 = 1 1/2
7/2 = 3 1/2
|
4/3 = 1 1/3
5/3 = 1 2/3
|
13/10 = 1 3/10
21/10 = 2 1/10
|
Завдання 1046
Які з неправильних дробів дорівнюють натуральному числу:
37/17, 45/45 = 1, 100/20 = 5, 70/30, 12/4 = 3, 36/20, 11/44
Завдання 1047 Скорочення дроби
|
3/12 = 1/4
11/22 = 1/2
|
4/24 = 1/6
10/18 = 5/9
|
20/40 = 1/2
21/36 = 7/12
|
15/25 = 3/5
|
Завдання 1048
Накресли квадрат, сторона якого дорівнює 3 см. Поділи його на 9 рівних частин. Зафарбуй 2 частини зеленим, а 5 частин синім кольором. Перевір рівності.
2/9 + 5/9 = 7/9
9/9 – 7/9 = 2/9
Завдання 1049
|
а) 3/8 + 1/8 = 4/8 = 1/2
1/8 + 5/8 = 6/8 = 3/4
в) 5/9 + 2/9 = 7/9
4/9 + 2/9 = 6/9 = 2/3
|
б) 4/12 + 7/12 = 11/12
1/12 + 5/12 = 6/12 = 1/2
г) 7/8 + 1/8 = 8/8 = 1
1/9 + 7/9 = 8/9
|
Завдання 1050
|
а) 5/12 + 5/12 = 10/12 = 5/6
5/21 + 5/21 = 10/21
в) 11/23 + 12/23 = 23/23 = 1
11/46 + 12/46 = 23/46
|
б) 4/13 + 3/13 = 7/13
4/31 + 3/31 = 7/31
г) 5/43 + 4/43 = 9/43
5/93 + 4/93 = 9/93 = 3/31
|
Завдання 1051, 1052
|
а) 1/8 + 2/8 + 3/8 = 6/8 = 3/4
б) 5/11 + 2/11 + 3/11 = 10/11
в) 12/14 + 3/14 + 6/14 = 21/14 = 3/2
|
а) 1/7 + 3/7 + 3/7 = 7/7 = 1
б) 6/13 + 6/13 + 4/13 = 16/13
в) 7/25 + 14/25 + 4/25 = 25/25 = 1
|
Завдання 1053, 1054
|
а) 4/7 – 2/7 = 2/7
5/7 – 3/7 = 2/7
б) 5/12 – 3/12 = 2/12 = 1/6
11/12 – 5/12 = 6/12 = 1/2
в) 9/12 – 7/12 = 2/12 = 1/6
5/13 – 1/13 = 4/13
г) 17/12 – 5/12 = 12/12 = 1
29/13 – 16/13 = 13/13 = 1
|
а) 18/19 – 7/19 = 11/19
25/19 – 15/19 = 10/19
б) 15/21 – 8/21 = 7/21 = 1/3
45/21 – 3/21 = 42/21 = 2
в) 11/35 – 6/35 = 5/35 = 1/7
74/35 – 47/35 = 27/35
г) 9/21 – 6/21 = 3/21 = 1/7
70/35 – 35/35 = 35/35 = 1
|
Завдання 1055
|
а) 13/27 + 7/27 = 20/27
б) 39/45 – 23/45 = 16/45
в) 17/54 – 9/54 = 8/54 = 4/27
|
г) 8/49 + 35/49 = 43/49
ґ) 79/40 – 51/40 = 28/40 = 7/10
д) 20/73 + 40/73 = 60/73
|
Завдання 1056
Координати точок: А(1 1/4), В(2 3/4) і С(5 1/2)
Завдання 1057 Запиши у вигляді неправильного дробу:
|
а) 7 5/21 = 152/21
б) 11 2/9 = 101/9
в) 15 39/40 = 639/40
|
г) 18 7/25 = 457/25
ґ) 20 11/37 = 751/37
д) 35 51/80 = 2851/80
|
Завдання 1058 Запиши у вигляді мішаного числа:
|
а) 45/8 = 5 5/8
б) 29/28 = 1 1/28
в) 135/13 = 10 5/13
г) 64/12 = 5 4/12 = 5 1/3
|
ґ) 97/29 = 3 10/29
д) 236/15 = 15 11/15
е) 512/53 = 9 35/53
|
Завдання 1059, 1060
|
а) 4 2/9 + 1/9 = 4 3/9
б) 2 3/8 + 1 4/8 = 3 7/8
в) 7 1/10 + 1 3/10 = 8 4/10
г) 2 + 7/6 = 2 7/6
ґ) 4 + 9/7 = 4 9/7
д) 7/11 + 8/11 = 15/11 = 1 4/11
|
а) 1 5/12 + 2 11/12 = 7 16/12 = 8 4/12
б) 3 7/13 + 2 7/13 = 5 14/13 = 6 1/13
в) 4 4/15 + 7 13/15 = 11 17/15 = 12 2/15
г) 8/9 + 7/9 = 15/9
ґ) 7/12 + 11/12 = 18/12 = 1 6/12
д) 8/15 + 11/15 = 19/15 = 1 4/15
|
Завдання 1061, 1062
|
а) 21/10 – 3/10 = 18/10 = 1 8/10
б) 45/22 – 3/22 = 42/22 = 1 20/22
в) 83/31 – 19/31 = 64/31 = 2 2/31
г) 3 5/9 – 4/9 = 3 1/9
ґ) 7 9/11 – 5 3/11 = 2 6/11
д) 6 4/13 – 2 1/13 = 4 3/13
|
а) 2 3/7 – 1/7 = 2 2/7
б) 5 3/4 – 2 2/4 = 3 1/4
в) 7 7/13 – 3 5/13 = 4 2/13
г) 73/25 – 13/25 = 60/25 = 2 10/25
ґ) 73/50 – 9/50 = 64/50 = 1 14/50
д) 198/49 – 19/49 = 179/49 = 3 32/49
|
Завдання 1063, 1064
|
а) 7 – 3/5 = 6 5/5 – 3/5 = 6 2/5
б) 5 – 27/31 = 4 31/31 – 27/31 = 4 4/31
в) 3 – 21/31 = 2 31/31 – 21/31 = 2 10/31
г) 4 – 20/63 = 3 63/63 – 20/63 = 3 43/63
|
а) 2 – 4/7 = 1 7/7 – 4/7 = 1 3/7
б) 7 – 18/43 = 6 43/43 – 18/43 = 6 25/43
в) 10 – 13/20 = 9 20/20 – 13/20 = 9 7/20
г) 17 – 16/35 = 16 35/35 – 16/35 = 16 19/35
|
Завдання 1065
Діти купили печиво, цукерки та фрукти. На печиво вони витратили 2/7, а на цукерки — 3/7 витрачених грошей. Яку частину грошей вони витратили на фрукти?
Розв'язання
7/7 – 2/7 – 3/7 = 2/7
Відповідь: 2/7 частину грошей вони витратили на фрукти.
Завдання 1066
Туристи були у поході три дні. За перший день вони пройшли 3/11 , а за другий — 4/11 усього маршруту. Яку частину маршруту вони пройшли за третій день?
Розв'язання
11/11 – 3/11 – 4/11 = 4/11
Відповідь: 4/11 частину частину маршруту вони пройшли за третій день.
Завдання 1067
|
а) x − 3/12 = 11/12
х = 11/12 + 3/12
х = 14/12
х = 1 2/12
|
б) 1 5/12 + x = 3 7/12
x = 3 7/12 − 1 5/12
x = 2 2/12
|
в) 5 3/7 – x = 1 1/7
x = 5 3/7 – 1 1/7
x = 4 2/7
|
Завдання 1068
|
а) 15/16 – х = 11/16
х = 15/16 – 11/16
х = 4/16
|
б) 2 2/5 + х = 3 4/5
х = 3 4/5 – 2 2/5
х = 1 2/5
|
в) x − 5/7 = 2 3/7
x = 2 3/7 + 5/7
x = 2 8/7
х = 3 1/7
|
Завдання 1069
Маса одного пакунка становить 2 2/5 кг, а другого — на 1 1/5 кг більша. Яка маса двох пакунків?
Розв'язання
1) 2 2/5 + 1 1/5 = 3 3/5 (кг) – маса другого пакунка;
2) 2 2/5 + 3 3/5 = 5 5/5 = 6 (кг) – маса двох пакунків.
Відповідь: 6 кг.
Завдання 1070
З одного поля фермер зібрав 15 7/13 т картоплі, а з другого — на 3 2/13 т менше. Скільки всього картоплі він зібрав?
Розв'язання
1) 15 7/13 – 3 2/13 = 12 5/13 (кг) – зібрав з другого поля;
2) 15 7/13 + 12 5/13 = 27 12/13 – зібрав з двох полів.
Відповідь: 27 12/13 кг.
Завдання 1071 На координатному промені познач точки з координатами:
А(1 1/5 ), В(2 3/5), С(7/5), D(17/5)
1 1/5 = 1 2/10
2 3/5 = 2 2/10
7/5 = 1 2/5 = 1 4/10
17/5 = 3 2/5 = 3 4/10
Завдання 1072 Покажи на частинах круга, виліпленого з пластиліну, що:
|
1/8 + 1 7/8 = 2
 +   = |
|
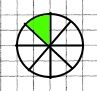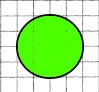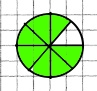1 1/8 + 1 2/8 = 2 3/8
+  =  |
|
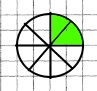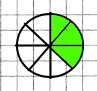2 – 3/8 = 1 5/8
- =  |
Завдання 1073
а) 17/21 – 3/21 – 7/21 = 7/21
б) 3/17 + 15/17 – 1/17 = 17/17 = 1
Завдання 1074
а) 12 3/7 + 10 2/7 – 4/7 = 22 5/7 – 4/7 = 22 1/7
б) 7 8/9 + 5/9 – 2 1/9 = 5 12/9 = 6 3/9
Завдання 1075
а) 5 1/3 – 3 2/3 = 4 4/3 – 3 2/3 = 1 2/3
б) 72 – 5 7/9 = 71 9/9 – 5 7/9 = 66 2/9
в) 29 1/8 – 10 7/8 = 28 9/8 – 10 7/8 = 18 2/8
Завдання 1076
а) 3/5 + (2 1/5 – 1 2/5) = 3/5 + (1 6/5 – 1 2/5) = 3/5 + 4/5 = 7/5 = 1 2/5
б) 3 2/7 – (2 1/7 – 1 4/7) = 3 2/7 – (1 8/7 – 1 4/7) = 3 2/7 – 4/7 = 2 9/7 – 4/7 = 2 5/7
в) 12 1/4 – (3 3/4 + 3 3/4) = 12 1/4 – 6 6/4 = 10 9/4 – 6 6/4 = 4 3/4
г) 7 7/8 – (2 3/8 + 1 7/8) = 7 7/8 – 3 10/8 = 6 15/8 – 3 10/8 = 3 5/8
Завдання 1077
а) 9 2/11 – (4 5/11 + 2 6/11) = 9 2/11 – 6 11/11 = 9 2/11 – 7 = 2 2/11
б) (5/6 + 4 2/6) – (3 2/5 – 2/5) = 4 7/6 – 3 = 1 7/6 = 2 1/6
Завдання 1078
а) 2/7 + 3/8 + 5/7 + 1/8 = (2/7 + 5/7) + (3/8 + 1/8) = 7/7 + 4/8 = 1 + 4/8 = 1 4/8
б) 5/13 + 4/3 + 2/3 + 8/13 = (5/13 + 8/13) + (4/3 + 2/3) = 13/13 + 6/3 = 1 + 2 = 3
Завдання 1079
Різниця двох чисел дорівнює 5/8 , зменшуване — 1 3/8. Знайди від’ємник.
Розв'язання
Нехай від'ємник дорівнює х. Складаємо рівняння:
1 3/8 – х = 5/8
х = 1 3/8 – 5/8
х = 11/8 – 5/8
х = 6/8
Відповідь: 6/8
Завдання 1080
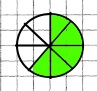Розв'язання
2 1/5 + 2 1/5 + 3 2/5 + 3 2/5 = 10 6/5 = 11 1/5 (м) – периметр прямокутника.
Відповідь: 11 1/5 м.
Завдання 1081
Основа рівнобедреного трикутника — 3/4 м, а бічна сторона на 1/4 м довша. Знайди його периметр.
Розв'язання
У рівнобедреному трикутнику бічні сторони рівні.
1) 3/4 + 1/4 = 4/4 = 1 (м) – довжина бічної сторони;
2) 3/4 + 1 + 1 = 2 3/4 (м) – периметр рівнобедреного трикутника.
Відповідь: 2 3/4 м.
Завдання 1082 Рівняння
|
а) (5/8 + х) + 3/8 = 11/8
5/8 + х = 11/8 – 3/8
5/8 + х = 8/8
х = 8/8 – 5/8
х = 3/8
|
б) (4 – х) + 2/3 = 1 1/3
4 – х = 1 1/3 – 2/3
4 – х = 4/3 – 2/3
4 – х = 2/3
х = 4 – 2/3
х = 3 3/3 – 2/3
х = 3 1/3
|
Завдання 1083 Яким числом треба замінити x, щоб рівність була правильною:
|
а) x/13 – 5/13 = 2/13
(х – 5)/13 = 2/13
х – 5 = 2
х = 2 + 5
х = 7
|
б) 17/25 – х/25 = 6/25
(17 – х)/25 = 6/25
17 – х = 6
х = 17 – 6
х = 11
|
в) 38/17 – х/17 = 1
(38 – х)/17 = 17/17
38 – х = 17
х = 38 – 17
х = 21
|
Завдання 1084 Які натуральні числа задовольняють нерівність:
а) 1/8 < x/8 < 5/8, тому 1 < x < 5, якщо х = 2, 3, 4
б) 1 1/3 < x/3 ≤ 2 2/3, 4/3 < x/3 ≤ 8/3, тому 4 < x ≤ 8, якщо х = 5, 6, 7, 8
в) 1 17/19 19 ≤ x/19 ≤ 2 1/19, 36/19 ≤ x/19 ≤ 39/19, якщо х = 36, 37, 38, 39
Завдання 1085, 1086 Яке натуральне число задовольняє нерівність:
|
а) x < 27/5, x < 5 2/5, х = 5
б) x < 234/13, х x < 18, х = 17
в) x ≤ 125/21, x ≤ 5 20/21, х = 5
|
а) x ≥ 39/4, x ≥ 9 3/9, х = 9
б) x > 360/24, x > 15, х = 14
в) x ≥ 578/17, x ≥ 34, х = 34
|
Завдання 1087
До магазину завезли моркву, буряк і картоплю. Морква становила 4/9 , а буряк — 2/9 завезених овочів. Скільки всього кілограмів овочів завезли до магазину, якщо картоплі було 180 кг?
Розв'язання
1) 9/9 – 4/9 – 2/9 = 3/9 = 1/3 – завезених овочів становить картопля;
2) 180 кг становить 1/3 частину всіх овочів, тому
180 : 1 • 3 = 540 (кг) – всього овочів завезли.
Відповідь: 540 кг.
Завдання 1088
Під час ремонту на вікна витратили 1/10, на стіни — 7/10 всієї фарби, а решту — 6 кг — витратили на підлогу. Скільки було фарби? Скільки витратили на: а) вікна; б) стіни?
Розв'язання
1) 10/10 – 1/10 – 7/10 = 2/10 = 1/5 – частину фарби витратили на підлогу;
2) 6 кг становить 1/5 частину всієї фарби, тому
6 : 1 • 5 = 30 (кг) – було фарби;
3) 30 : 10 • 1 = 3 (кг) – витратили фарби на вікна;
4) 30 : 10 • 7 = 21 (кг) – витратили фарби на підлогу.
Відповідь: 30 кг; 3 кг; 21 кг.
Завдання 1089 Порівняйте значення виразів A і B, якщо:
а) A = 8 2/7 – (4 5/11 + 2 6/11) = 8 2/7 – 6 11/11 = 8 2/7 – 7 = 1 2/7
B = 6 2/7 – (3 7/12 + 1 5/12) = 6 2/7 – 4 12/12 = 6 2/7 – 5 = 1 2/7
1 2/7 = 1 2/7, A = B
б) A = 5 4/9 + 3 5/9 – 2 1/5 = 8 9/9 – 2 1/5 = 9 – 2 1/5 = 8 5/5 – 2 1/5 = 6 4/5
B = 4 7/9 + 5 2/9 – 2 4/5 = 9 9/9 – 2 4/5 = 10 – 2 4/5 = 9 5/5 – 2 4/5 = 7 1/5
6 4/5 < 7 1/5, A < B
Завдання 1090
Після прожарювання отримали 33 кг кавових зерен. Скільки кілограмів сирих зерен потрібно було взяти, якщо під час прожарювання втрачається чверть їх маси?
Розв'язання
1) 1 – 1/4 = 3/4 – частину становлять зерна після прожарювання;
2) 33 кг становить 3/4 сирих зерен, тому
33 : 3 • 4 = 44 (кг) – потрібно сирих зерен.
Відповідь: 44 кг.
Завдання 1091
х • 2 + 96 : 2 = 108
х • 2 + 48 = 108
х • 2 = 108 – 48
х • 2 = 60
х = 60 : 2
х = 30
Завдання 1092
На складі є цвяхи в ящиках по 16, 17 і 40 кг. Чи можна взяти зі складу 100 кг цвяхів, не розкриваючи жодного ящика?
Треба сумувати парні числа, а непарні парне число разів, тому
17 + 17 + 17 + 17 + 16 + 16 = 100
Завдання 1093
|
а) 32 • (x + 4) = 160
32х + 128 = 160
32х = 160 – 128
32х = 32
х = 32 : 32
х = 1
|
б) 48 • (x – 8) = 240
48x – 384 = 240
48x = 240 + 384
48x = 624
х = 624 : 48
х = 13
|
Завдання 1094
Знайди два числа, сума яких дорівнює 105 і одне з яких:
|
а) більше за друге на 15;
Розв'язання
Нехай перше число х, тоді друге (х + 15)
х + х + 15 = 105
2х = 105 – 15
2х = 90
х = 90 : 2
х = 45 – перше число;
45 + 15 = 60 – друге число.
Відповідь: 45 і 60.
|
б) удвічі більше за друге число.
Розв'язання
Нехай друге число х, тоді перше 2х
2х + х = 105
3х = 105
х = 105 : 3
х = 35 – друге число;
35 • 2 = 70 – перше число.
Відповідь: 70 і 35.
|
Завдання 1095
Знайди довжину бічної сторони рівнобедреного трикутника, якщо його периметр більший за основу на 10 м.
Розв'язання
Оскільки 10 м — це сума довжин двох рівних бічних сторін рівнобедреного трикутника, тому
10 : 2 = 5 (м)
Відповідь: довжина бічної сторони рівнобедреного прямокутника 5 м.