ГДЗ робочий зошит 3 клас Козак, Корчевська сторінка 3 - 10 математика частина 2

Серія "Вчимось разом" до робочого зошита

"Математика 3 клас Козак М., Корчевська О. (частина 2)"

Сторінка 3

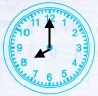
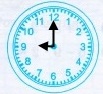
Завдання 1 Доба

Годинник
Час до полудня	8 год
Час після полудня	8 год + 12 год = 20 год

Відповідь: 8 год або 20 год

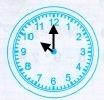
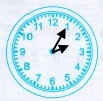
Завдання 2

Електронний годинник	22 год
Механічний годинник
Час	10 год після полудня

Відповідь: 10 год після полудня

Завдання 3 Днів у кожному місяці

Пароплав відійшов від пристані о 21 год 29 квітня і був у плаванні 2 доби 1 год. Якого числа і місяця та о котрій годині він прибув до пункту призначення?

^{Міркуємо так. 29 + 2 = 30 + 1 прибув 1 травня. 21 + 1 = 22 (год) – час прибуття.}

Відповідь: 1 травня о 22 год

Завдання 4 Складена задача на ділення на вміщення

Для обстеження невідомих берегів моряки підготували кілька шестивеслових човнів і 2 — восьмивеслові, а всього на них встановили 40 весел. Скільки було шестивеслових човнів?

^Човни	^{Весел на 1 човні}	^{Кількість човнів}	^{Загальна кількість весел}
^{Шестивеслові}	⁶	^?	^?	^{40 весел}
^{Восьмивеслові}	⁸	²	^?	^{40 весел}

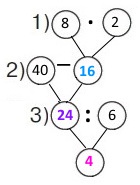
^{Вираз (40 – 8 • 2) : 6}

^{План розв’язування}

^{1) Загальна кількість весел на восьмивеслових човнах?}

^{2) Загальна кількість весел на шестивеслових човнах?}

^{3) Скільки було шестивеслових човнів?}

1) 8 • 2 = 16 (в.) – весел на восьмивеслових човнах разом.

2) 40 – 16 = 24 (в.) – весел на шестивеслових човнах разом.

3) 24 : 6 = 4 (ч.) – було шестивеслових човнів.

Відповідь: було 4 шестивеслових човнів.

Завдання 5 Порядок дій

(16 – 7 ) • (2 + 4) = 54

^{1) 16 – 7 = 9}

^{2) 2 + 4 = 6}

^{3) 9 • 6 = 54}

1 + 6 • 4 + 5 = 30

^{1) 6 • 4 = 24}

^{2) 1 + 24 = 25}

^{3) 25 + 5 = 30}

16 – 7 • 2 + 4 = 6

^{1) 7 • 2 = 14}

^{2) 16 – 14 = 2}

^{3) 2 + 4 = 6}

1 + 6 • (4 + 5) = 55

^{1) 4 + 5 = 9}

^{2) 6 • 9 = 54}

^{3) 1 + 54 = 55}

80 – 64 : 8 : 2 = 76

^{1) 64 : 8 = 8}

^{2) 8 : 2 = 4}

^{3) 80 – 4 = 76}

(80 – 64) : 8 : 2 = 1

^{1) 80 – 64 = 10 + (70 – 64) = 16}

^{2) 16 : 8 = 2}

^{3) 2 : 2 = 1}

Завдання 6 Одиниці вимірювання

^{10 м = 100 дм}

^{100 см = 10 дм}

^{306 кг < 3 ц 60 кг}^{(3 ц 6 кг < 3 ц 60 кг)}

^{8 грн 1 к. > 81 к.}^{(801 к. > 81 к.)}

^{800 мм > 8 см}^{(80 см > 8 см)}

^{4 дм > 7 см 9 мм}^{(40 см > 7 см 9 мм)}

Сторінка 4

Завдання 1

^{Годинник}

^{Час до полудня}

6 год

11 год

7 год

9 год

^{Час після полудня}

^{6 год + 12 год =}

18 год

^{11 год + 12 год =}

23 год

^{7 год + 12 год =}

19 год

^{9 год + 12 год =}

21 год

Завдання 2

Шлях мурашки: угору — 1 см; праворуч — 9 см; униз — 1 см; ліворуч — 9 см.

^{Міркуємо так: її шляхом буде прямокутник довжиною 9 см і шириною 1 см.}

Завдання 4 Рівняння

780 – х = 290

х = 780 – 290

х = 490

Перевірка

780 – 490 = 290

290 = 290

Завдання 5 Задача на зведення до одиниці

Місткість 8 однакових акваріумів — 72 л. Яка місткість 5 таких акваріумів?

^{Літрів у 1 акваріумі}	^{Кількість акваріумів}	^{Загальна кількість літрів}
^?	⁸	⁷²
^{однакова}	⁵	^?

^{Короткий запис}

^{4 години —}^{28 центнерів}

^{? години — 56 центнерів}

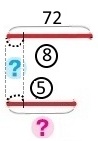
^{План розв'язування}

^{1) Яка місткість 1 такого акваріума?}

^{2) Яка місткість 5 таких акваріумів?}

Розв'язання

1) 72 : 8 = 9 (л) – місткість 1 такого акваріума.

2) 9 • 5 = 45 (л) – місткість п’яти таких акваріумів.

Вираз: 72 : 8 • 5

Відповідь: місткість п’яти таких акваріумів 45 літрів.

Завдання 6

^{500 – 340 + 80 = 500 + 80 – 340 = 580 – 340 =}²⁴⁰

^{500 – (340 + 80) = 500 – (340 + 60 + 20) = 500 – 420 =}⁸⁰

^{910 – (600 – 150) = 910 – 600 + 150 = 310 + 150 =}⁴⁶⁰

^{910 – 600 – 150 = 310 – 150 = 310 – 200 + 50 =}¹⁶⁰

Сторінка 5

Завдання 1

(300 – 260) : 5 • 9 = 72

1) 300 – 260 = 40

2) 40 : 5 = 8

3) 8 • 9 = 72

190 + 4 • 5 – 60 = 150

1) 4 • 5 = 20

2) 190 + 20 = 190 + 10 + 10 = 210

3) 210 – 60 = 210 – 100 + 40 = 150

300 – 48 : 8 • 5 = 270

1) 48 : 8 = 6

2) 6 • 5 = 30

3) 300 – 30 = 270

(16 – 8) • (14 – 7) = 56

1) 16 – 8 = 8

2) 14 – 7 = 7

3) 8 • 7 = 56

Завдання 2 Складена задача на зменшення на деяке число

Песики Сірко, Рябко і Бровко шукали загублені речі. Сірко знайшов згубу за 2 хв 10 с, Рябко затратив часу на 20 с більше, а Бровко — на 1 хв менше, ніж Рябко. Скільки часу затратив Бровко на пошук загубленої речі?

^{Короткий запис}

^{Сірко — 2 хв 10 с}

^{Рябко —}^?^{, на 20 с більше, ніж Сірко}

^{Бровко —}^?^{, на 1 хв менше, ніж Рябко}

^{План розв’язування}

^{1) Скільки часу затратив на пошук Рябко?}

^{2) Скільки часу затратив Бровко на пошук загубленої речі?}

Розв’язання

1) 2 хв 10 с + 20 с = 2 хв 30 с – час затратив Рябко.

2) 2 хв 30 с – 1 хв = 1 хв 30 с – час затратив Бровко.

^{1 хв 30 с = 60 с + 30 с = 90 с}

Відповідь: 1 хв 30 с, або 90 с

Завдання 3

У дитячому таборі двічі організовували триденний похід у гори: першого разу — 28 червня, а другого разу — 28 липня. Визнач за календарем дату завершення кожного походу.

^{Міркуємо так: 28 + 3 = 30 + 1 для червня, оскільки червень має 30 днів, то похід завершиться 1 липня; 28 + 3 = 31 для липня, оскільки липень має 31 день.}

Відповідь: першого разу – 1 липня,

а другого разу — 31 липня

Завдання 4 Задача на зведення до одиниці

Маса 9 цеглин 27 кг. Скільки таких цеглин можуть важити 21 кг?

^{Маса 1 цеглини}	^{Кількість цеглин}	^{Загальна маса}
^?	⁹	^{27 кг}
^{однакова}	^?	^{21 кг}

^{Короткий запис}

^{9 цеглин — 27 кг}

^{? цеглин — 21 кг}

^{План розв’язування}

^{1) Яка маса одної цеглини? 27 : 9 = 3 (кг)}

^{2) Скільки таких цеглин можуть важити 21 кг? 21 : 3 = 7 (ц.)}

Розв’язання

1) 21 : (27 : 9) = 7 (ц.)

Відповідь: двадцять один кілограм можуть важити 7 таких цеглин.

Завдання 5

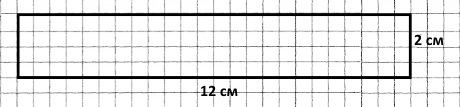
Накресли прямокутник, довжина якого становить 1 дм 2 см, а ширина — у 6 разів коротша.

^{Міркуємо так. 1 дм 2 см = 12 см, тоді 12 см : 6 = 2 см – ширина прямокутника.}

^{Треба накреслити прямокутник довжиною 12 см і шириною 2 см.}

Сторінка 6

Завдання 1

8 ц 40 кг = 800 кг + 40 кг = 840 кг

5 м З см = 500 см + 3 см = 503 см

8 ц 4 кг = 800 кг + 4 кг = 804 кг

5 м 30 см = 500 см + 30 см = 530 см

100 хв = 60 хв + 40 хв = 1 год 40 хв

150 с = 120 с + 30 с = 2 хв 30 с

50 год = 48 год + 2 год = 2 доби 2 год

1 хв 40 с = 60 с + 10 с = 100 с

Завдання 2 Переведи у 24-годинний відлік часу

^{3 год дня —> 3 год + 12 год =}¹⁵^год

^{12 год ночі —> 12 год + 12 =}²⁴^год

^{7 год вечора —> 7 год + 12 год =}¹⁹^год

^{11 год ночі —> 11 год + 12 год =}²³^год

Завдання 3 Переведи у 12-годинний відлік часу.

14 год —> 2 год дня 20 год —> 8 год вечора

Завдання 4 Ознайомлення з дробами

^{Замальовано частин}	1	1	1	1	1	1
^{Всього частин}	4	4	9	4	8	8
^Дріб	1/4	1/4	1/9	1/4	1/8	1/8
^{Читаємо}	^чверть	^{одна четверта}	^{одна дев’ята}		^{одна восьма}

Завдання 5 Складена задача на кратне порівняння добутків

У скільки разів місткість чотирьох 2-літрових глечиків менша, ніж місткість восьми 9-літрових бідонів?

^{Короткий запис}

^{Глечики —}^?^{л, 4 глечики по 2 л; у}^?^{разів менше}

^{Бідони —}^?^{л, 8 бідонів по 9 л}

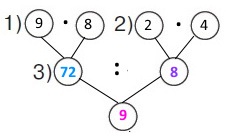
^{Короткий запис №1}

^{Глечики —}^?^{л, 4 глечики по 2 л}

^{Короткий запис №2}

^{Бідони —}^?^{л, 8 бідонів по 9 л}

^{Короткий запис №3}

^{Глечики —}⁸^{л, у}^?^{разів менше}

^{Бідони —}⁷²^л

^{План розв’язування}

^{1) Яка місткість чотирьох глечиків? 2 • 4 = 8 (л)}

^{2) Яка місткість восьми бідонів? 9 • 8 = 72 (л)}

^{3) У скільки разів місткість чотирьох глечиків менша, ніж місткість восьми бідонів? 72 : 8 = 9 (разів)}

Розв’язання

Вираз (9 • 8) : (2 • 4) = 9 разів

Відповідь: у 8 разів менша місткість глечиків, ніж бідонів.

Завдання 6 Складена задача на різницеве порівняння

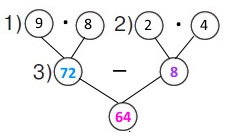
На скільки літрів місткість чотирьох 2-літрових глечиків менша, ніж місткість восьми 9-літрових бідонів?

^{Короткий запис}

^{Глечики —}^?^{л, 4 глечики по 2 л; на}^?^{л менше}

^{Бідони —}^?^{л, 8 бідонів по 9 л}

^{Короткий запис №1}

^{Глечики —}^?^{л, 4 глечики по 2 л}

^{Короткий запис №2}

^{Бідони —}^?^{л, 8 бідонів по 9 л}

^{Короткий запис №3}

^{Глечики —}⁸^{л, на}^?^{л менше}

^{Бідони —}⁷²^л

^{План розв’язування}

^{1) Яка місткість чотирьох глечиків? 2 • 4 = 8 (л)}

^{2) Яка місткість восьми бідонів? 9 • 8 = 72 (л)}

^{3) На скільки літрів місткість чотирьох глечиків менша, ніж місткість восьми бідонів? 72 - 8 = 64 (л)}

Розв’язання

Вираз: (9 • 8) – (2 • 4) = 64 (л)

Відповідь: на 64 літри менша місткість глечиків, ніж бідонів.

Сторінка 7

Завдання 1

^{Серед дробів з однаковими чисельниками більший (менший) той дріб, у якого менший (більший) знаменник.}

1/4 > 1/6 1/4 < 1/3 1/6 < 1/3 1/4 < 1/2

Завдання 2

^{Записати дроби з однаковими чисельниками у порядку зменшення – це означає записати їх у порядку збільшення знаменників.}

1/2, 1/4, 1/6, 1/8, 1/9, 1/11, 1/20

Завдання 3

1/100 м = 1 см

^{(бо 1 м = 100 см)}

1/10 м = 1 дм

^{(бо 1 м = 10 дм)}

1/100 дм = 1 мм

^{(бо 1 дм = 10 см = 100 мм)}

1/1000 м = 1 мм

^{(бо 1 м = 100 см = 1000 мм)}

Завдання 4 Складена задача на кратне порівняння числа і різниці

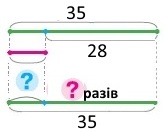
На будівництво фортеці діти витратили 35 цеглинок LEGO, а на будівництво гаража — на 28 менше. У скільки разів менше цеглинок вони витратили на будівництво гаража, ніж на фортецю?

^{Короткий запис}

^{Фортеця — 35 цеглинок}

^{Гараж —}^?^{, на 28 цеглинок менше; у}^?^{разів менше}

^Вираз^{35 : (35 – 28)}

^{Короткий запис №1}

^{Фортеця — 35 цеглинок}

^{Гараж —}^?^{, на 28 цеглинок менше}

^{Короткий запис №2}

^{Фортеця — 35 цеглинок}

^{Гараж —}⁷^{цеглинок, у}^?^{разів менше}

^{План розв’язування}

^{1) Скільки цеглинок витратили на будівництво фортеці?}

^{2) У скільки разів менше цеглинок вони витратили на будівництво гаража, ніж на фортецю?}

Розв’язання

1) 35 – 28 = 7 (ц.) – цеглинок витратили на будівництво фортеці.

2) 35 : 7 = 5 (разів) – у стільки разів менше цеглинок витратили на будівництво гаража, ніж на фортецю.

Вираз: 35 : (35 – 28)

Відповідь: у 5 разів менше цеглинок витратили на будівництво гаража, ніж на фортецю.

Завдання 4

Накресли три різні ламані з початком у точці А, кожна з яких має довжину 10 см.

^{Міркуємо так. 10 см = 2 см + 8 см – ламана з двох ланок. 10 см = 5 см + 5 см – ламана з двох ланок. 10 см = 3 см + 3 см + 4 см – ламана з трьох ланок.}

Сторінка 8

Завдання 1

Число	24	12	20	28	Число	20	35	45	30
1/4 числа	6	3	5	8	1/5 числа	4	7	9	6

Завдання 2

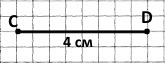
АВ = 12 см

Побудували відрізок CD, довжина якого дорівнює 1/3 довжини відрізка АВ.

12 см : 3 = 4 см – довжина відрізка CD.

Завдання 3 Складена задача на зменшення на деяке число зі змінною

^{Маса І мішка}^{b кг, а другого – у 6 разів більша. Маса ІІІ мішка на 14 кг більша, ніж ІІ. Яка маса ІІІ мішка?}

^{Короткий запис}

^{І —}^{b кг}

^{ІІ — ?, у 6 разів більше, ніж І}

^{III — ?, на 14 кг менше, ніж ІІ}

^{Міркуємо так.}^{b • 6 (кг) – І,}^{b • 6 – 14 (кг) – ІІ.}

Вираз: b • 6 – 14 (кг)

• Якщо b = 7, тоді b • 6 – 14 = 7 • 6 – 14 = 42 – 14 = 42 – 12 – 2 = 28 (кг)

Відповідь: 28 кілограмів.

Завдання 4

7 • 8 – (520 – 480) = 16

^{1) 7 • 8 = 56}

^{2) 520 – 480 = 520 – 500 + 20 = 40}

^{3) 56 – 40 = 16}

636 – (6 • 6 + 500) = 100

^{1) 6 • 6 = 36}

^{2) 36 + 500 = 536}

^{3) 636 – 536 = 100}

700 + 9 • 9 – 80 = 701

^{1) 9 • 9 = 81}

^{2) 700 + 81 = 781}

^{3) 781 – 80 = 701}

472 – 9 • 8 + 380 = 780

^{1) 9 • 8 = 72}

^{2) 472 – 72 = 400}

^{3) 400 + 380 = 780}

Завдання 5

^{Оскільки у дробів однакові чисельники їх треба впорядкувати в порядку зменшення знаменників.}

Дроби в порядку їх збільшення: 1/100, 1/42, 1/20, 1/18, 1/16, 1/12

Сторінка 9

Завдання 1

^{1/6 від 1 доби = 1 доба : 6 = 24 год : 6 =}⁴^год

^{1/3 від 1 доби = 1 доба : 3 = 24 год : 3 =}⁸^год

^{1/5 від 1 см = 1 см : 5 = 10 мм : 5 =}²^мм

^{1/2 від 1 м = 1 м : 2 = 10 дм : 2 =}⁵^дм

^{1/2 від 1 дм = 1 дм : 2 = 10 см : 2 =}⁵^см

Завдання 2

^{Годинник}
^{Час до полудня}	2 год 5 хв	4 год 40 хв	11 год 55 хв	8 год 25 хв
^{Час після полудня}	14 год 5 хв	16 год 40 хв	12 год 55 хв	20 год 25 хв

Завдання 3 Складена задача на знаходження суми часток

Галинка сплела віночок із 24 польових квіток. Маки становили 1/4 квіток, а волошки – 1/3. Скільки маків і волошок разом використала Галинка?

^{Короткий запис}

^{Маки —}^?^{, 1/4 від 24 квіток}

^{Волошки —}^?^{, 1/3 від 24 квіток}

^{Всього —}^?

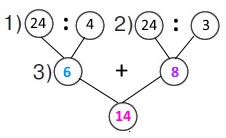
^{Вираз 24 : 4 + 24 : 3}

Розв’язання

1) 24 : 4 = 6 (м.) – маки.

2) 24 : 3 = 8 (в.) – волошки.

3) 6 + 8 = 14 (кв.) – маків і волошок разом використала Галинка.

Відповідь: Галинка використала разом 14 маків і волошок.

Завдання 4 Складена задача на знаходження частини числа

^{Маса першого мішка картоплі 64 кг. У другому мішку 1/8 від маси першого мішка, а в третьому – 1/2 від маси другого мішка. Яка маса третього мішка?}

^{Короткий запис}

^{І — 64 кг}

^{ІІ —}^?^{, 1/8 від І}

^{ІІІ —}^?^{, 1/2 від ІІ}

Розв’язання

1) 64 : 8 = 8 (кг) – маса І.

2) 8 : 2 = 4 (кг) – маса ІІ.

Відповідь: 4 кілограми.

Завдання 5

360 + (120 – 70) + 240 = 650

^{1) 120 – 70 = 120 – 100 + 30 = 50}

^{2) 360 + 50 = 360 + 40 + 10 = 410}

^{2) 410 + 240 = 650}

800 – (430 – 260) + 90 = 720

^{1) 430 – 260 = 430 – 300 + 40 = 170}

^{2) 800 – 170 = 800 – 200 + 30 = 630}

^{3) 630 + 90 = 630 + 70 + 20 = 720}

360 + 120 – (70 + 240) = 170

^{1) 70 + 240 = 240 + 60 + 10 = 310}

^{2) 360 + 120 = 480}

^{3) 480 – 310 = 170}

800 – 430 – (260 + 90) = 20

^{1) 260 + 90 = 260 + 40 + 50 = 350}

^{2) 800 – 430 = 800 – 500 + 70 = 370}

^{3) 370 – 350 = 20}

Сторінка 10

Завдання 1 Множення на розрядну одиницю

10 • 10 – 92 = 100 – 92 = 8 8 • 100 – 730 = 800 – 730 = 70 70 • 10 = 700

100 • 6 – 560 = 600 – 560 = 40 40 : 8 = 5 5 • 10 = 50 50 • 10 = 500

Завдання 2 Задача знаходження чисел за трьома сумами

У трьох класах 90 учнів. У першому і другому класах разом — 62 учні, а в другому і третьому — 61. Скільки учнів у кожному класі окремо?

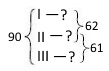
Розв’язання

1) 90 – 61 = 29 (уч.) – у І класі.

2) 62 – 29 = 33 (уч.) – учнів у ІІ класі.

3) 61 – 33 = 28 (уч.) – учнів у ІІІ класі.

Відповідь: у першому класі 29 учнів, у другому класі 33 учні, у третьому 28 учнів.

Завдання 3 Складена задача кратне і різницеве порівняння часток

Місткість З однакових відер — 24 л, а 5 каністр — 20 л. У скільки разів більша місткість відра, ніж каністри? На скільки літрів більша?

	^{Літрів у посудині}	^{Кількість посудин}	^{Загальна кількість літрів}
^Відро	^?^{, у}^?^{разів більше, на}^?^{л більше}	³	²⁴
^{Каністра}	^?	⁵	²⁰