© Барна Р., 2020
Серія "Вчимось разом" до підручника "Математика 3 клас Козак М., Корчевська О."
Завдання 338
16 • 6 = (10 + 6) • 6 = 60 + 36 = 96 96 : 12 = 8 8 • 9 = 72
72 : 24 = 72 : 8 : 3 = 9 : 3 = 3 3 • 270 = 3 • (200 + 70) = 600 + 210 = 810
810 : 90 = 810 : 10 : 9 = 9 9 • 11 = 90 + 9 = 99 99 + 1 = 10
Завдання 339 Рівності на ділення числа 96 на числа: 32; 24; 16; 12; 8; 6; 4; 3; 2.
96 : 32 = 3 96 : 24 = 4 96 : 16 = 6 96 : 12 = 8 96 : 8 = (80 + 16) : 8 = 10 + 2 = 12
96 : 6 = (60 + 36) : 6 = 10 + 6 = 16 96 : 4 = (80 + 16) : 4 = 20 + 4 = 24
96 : 3 = (90 + 6) : 3 = 30 + 2 = 32 96 : 2 = (80 + 16) : 2 = 40 + 8 = 48
Завдання 340 Ознайомлення з дробами
а) 1/6 від 18 = 18 : 6 = 3
б) 1/6 від числа дорівнює 18, тоді число 18 • 6 = 60 + 48 = 108
Завдання 341 Спосіб послідовного ділення
72 : 18 = 72 : (9 • 2) = 72 : 9 : 2 = 8 : 2 = 4
54 : 27 = 54 : (9 • 3) = 54 : 9 : 3 = 6 : 3 = 2
48 : 16 = 48 : (8 • 2) = 48 : 8 : 2 = 6 : 2 = 3
56 : 14 = 56 : (7 • 2) = 56 : 7 : 2 = 8 : 2 = 4
Завдання 342 Рівняння
|
80 : х = 5 х = 80 : 5 х = (50 + 30) : 5 х = 16 80 : 16 = 5 5 = 5 |
х : 80 = 5 х = 5 • 80 х = 400 400 : 80 = 400 : 10 : 8 = 5 5 = 5
|
Завдання 343 Дві рівності на ділення з остачею
17 : 5 = 3 (ост. 2) 17 : 3 = 5 (ост. 2)
Завдання 344 Задача на зведення до одиниці
У першому корпусі літнього табору в 10 однакових кімнатах мешкають 40 дітей. У другому корпусі в одній кімнаті мешкає дітей у 2 рази менше, ніж у кімнаті першого. На скільки дітей розрахований другий корпус, у якому 60 кімнат?
|
|
Дітей у 1 кімнаті |
Кількість кімнат |
Кількість дітей |
|
І корпус |
? |
10 |
40 |
|
ІІ корпус |
?, у 2 рази менше |
60 |
? |
Короткий запис
І корпус — 10 кімнат — 40 дітей, 1 кімната — ? дітей
ІІ корпус — 60 кімнат — ? дітей, 1 кімната — ?, у 2 рази менше
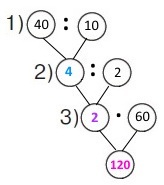
Вираз 40 : 10 : 2 • 60
План розв’язування
1) Скільки дітей в одній кімнаті першого корпусу?
2) Скільки дітей в одній кімнаті другого корпусу?
3) На скільки дітей розрахований другий корпус?
Розв’язання
1) 40 : 10 = 4 (д.) – дітей в одній кімнаті першого корпусу.
2) 4 : 2 = 2 (д.) – дітей в одній кімнаті другого корпусу.
3) 2 • 60 = 120 (д.) – на стільки дітей розрахований другий корпус.
Відповідь: другий корпус розрахований на 120 дітей.
Завдання 345 Обчисли значення виразу З • 5. Збільш перший множнику 2 рази; у 4 рази. Як змінюється добуток? У скільки разів?
3 • 5 = 15
(3 • 2) • 5 = (3 • 5) • 2 = 15 • 2 = 30 добуток збільшиться у 2 рази
(3 • 4) • 5 = (3 • 5) • 4 = 15 • 4 = 60 добуток збільшиться у 4 рази
Завдання 346
90 : 15 = 6 95 : 19 = 4 80 : 16 = 80 : 8 : 2 = 5 68 : 17 = 4
Завдання 347
12 : 3 = 4 (ост. 2) 12 : 4 = 3 (ост. 2)
Завдання 348
1/2 від 84 = 84 : 2 = (80 + 4) : 2 = 40 + 20 = 42
1/3 від 84 = 84 : 3 = (60 + 24) : 3 = 20 + 8 = 28
1/4 від 84 = 84 : 4 = (80 + 4) : 4 = 20 + 1 = 21
1/6 від 84 = 84 : 6 = (60 + 24) : 6 = 10 + 4 = 14
1/7 від 84 = 84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
1/12 від 84 = 84 : 12 = 7
Завдання 349
|
15 : 5 = 3 17 : 5 = 3 (ост. 2) |
21 : 7 = 3 25 : 7 = 3 (ост. 4) |
81 : 9 = 9 89 : 9 = 9 (ост. 8) |
40 : 10 = 4 48 : 10 = 4 (ост. 8) |
Завдання 350
Остачі від ділення чисел на 2: 0, 1
Остачі від ділення чисел на 3: 0, 1, 2
Остачі від ділення чисел на 4: 0, 1, 2, 3
Остачі від ділення чисел на 5: 0, 1, 2, 3, 4
Завдання 351
|
26 : 3 = 8 (ост. 2) 24 2 |
29 : 5 = 5 (ост. 4) 25 4 |
47 : 7 = 6 (ост. 5) 42 5 |
64 : 9 = 7 (ост. 1) 63 1 |
Завдання 352 Старий маяк має 9 поверхів.
9 : 3 = 3 (рази) – у стільки разів вище потрібно підійматися сходами на дев'ятий поверх, ніж на третій.
8 : 2 = 4 (рази) – у стільки разів вище потрібно підійматися сходами на восьмий, ніж на другий.
Завдання 353 Складена задача на віднімання
Маса контейнера з апельсинами 2 ц (200 кг). Порожній контейнер має масу 10 кг. З контейнера набрали 5 сіток, по 4 кг апельсинів у кожній. Скільки кілограмів апельсинів залишилось у контейнері?
|
Було |
Набрали |
Залишилося |
|
200 кг без 10 кг |
5 сіток по 4 кг |
? |
Короткий запис
Було — ?, 200 кг без 10 кг
Набрали — ? кг, 5 сіток по 4 кг
Залишилося — ?
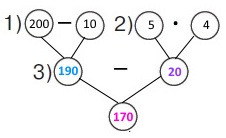
Вираз (200 – 10) – 5 • 4
План розв’язування
1) Скільки кілограмів апельсинів було у контейнері?
2) Скільки кілограмів апельсинів набрали?
3) Скільки кілограмів апельсинів залишилось у контейнері?
Розв’язання
1) 200 – 10 = 190 (кг) – кілограмів апельсинів було у контейнері.
2) 5 • 4 = 20 (кг) – кілограмів апельсинів набрали.
3) 190 – 20 = 170 (кг) – кілограмів апельсинів залишилось у контейнері.
Відповідь: у контейнері залишилося 170 кілограмів апельсинів.
Завдання 354 Складена задача на різницеве порівняння частин
В акваріумі плавало 72 рибки. Золоті рибки становили 1/4 частину усіх рибок, а сомики — 1/3. На скільки більше було в акваріумі сомиків, ніж золотих рибок?
Короткий запис
Золоті рибки — ?, 1/4 всього
Сомики — ?, 1/3 всього; на ? рибок більше
Всього — 72 рибки
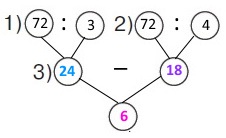
Вираз 72 : 3 – 72 : 4
План розв’язування
1) Скільки було золотих рибок?
2) Скільки було сомиків?
3) На скільки більше було в акваріумі сомиків, ніж золотих рибок?
Розв’язання
1) 72 : 4 = (40 + 32) : 4 = 18 (р.) – золотих рибок було.
2) 72 : 3 = (60 + 12) : 3 = 24 (р.) – сомиків було.
3) 24 – 18 = 24 – 20 + 2 = 6 (р.) – на стільки більше було в акваріумі сомиків, ніж золотих рибок.
Відповідь: на 6 сомиків більше, ніж золотих рибок.
Завдання 355
|
75 : 9 = 8 (ост. 3) |
48 : 7 = 6 (ост. 6) |
36 : 5 = 7 (ост. 1) |
49 : 6 = 8 (ост. 1) |
63 : 8 = 7 (ост. 7) |
Завдання 356
Множник • Множник = Добуток. Щоб знайти невідомий множник, треба добуток поділити на відомий множник
|
Множник |
9 |
42 : 6 = 7 |
3 |
17 |
80 : 10 = 8 |
16 |
23 |
15 |
|
Множник |
7 |
6 |
45 : 3 = 15 |
3 |
10 |
32 : 16 = 2 |
4 |
60 : 15 = 4 |
|
Добуток |
63 |
42 |
45 |
51 |
80 |
32 |
92 |
60 |
Завдання 357, 358 Виконали ділення з остачею та зробили перевірку:
44 : 7 = 6 (ост. 2) 2 < 7 6 • 7 + 2 = 42 + 2 = 44
27 : 5 = 5 (ост. 2) 2 < 5 5 • 5 + 2 = 25 + 2 = 27
33 : 6 = 5 (ост. 3) 3 < 6 5 • 6 + 3 = 30 + 3 = 33
77 : 8 = 9 (ост. 5) 5 < 8 9 • 8 + 5 = 72 + 5 = 77
Завдання 359 Складена задача на знаходження суми часток
Одна казка займає k сторінок, а інша — n. За скільки днів Віка прочитає ці дві казки, якщо буде читати по 8 сторінок в день?
1 спосіб
План розв’язування
1) За скільки днів Віка прочитає першу казку? k : 8 (дн.)
2) За скільки днів Віка прочитає другу казку? n : 8 (дн.)
3) За скільки днів Віка прочитає ці дві казки? k : 8 + n : 8 (дн.)
k : 8 + n : 8 (дн.)
Якщо k = 32, n = 64, тоді k : 8 + n : 8 = 32 : 8 + 64 : 8 = 4 + 8 = 12 (дн.)
2 спосіб
Оскільки читала однакову кількість сторінок, тому
План розв’язування
1) Скільки всього сторінок мають ці казки? k + n (стор.)
2) За скільки днів Віка прочитає ці дві казки? (k + n) : 8 (дн.)
(k + n) : 8 (дн.)
Якщо k = 32, n = 64, тоді (k + n) : 8 = (32 + 64) : 8 = 4 + 8 = 12 (дн.)
Відповідь: за 12 днів.
Завдання 360
|
х • 8 = 56 х = 56 : 8 х = 7 7 • 8 = 56 56 = 56 |
х : 4 = 17 х = 17 • 4 х = (10 + 7) • 4 х = 68 68 : 4 = 17 17 = 17 |
90 : х = 5 х = 90 : 5 х = (50 + 40) : 5 х = 18 90 : 18 = 5 5 = 5 |
Завдання 361 Задача на зведення до одиниці
На 4 шарфи потрібно 12 мотків шерсті. Скільки таких шарфів можна сплести з 15 мотків шерсті?
|
Мотків на 1 шарф |
Кількість шарфів |
Загальна кількість мотків |
|
? |
4 |
12 |
|
однаково |
? |
15 |
Короткий запис
4 шарфи — 12 мотків, 1 шарф — ? мотків
? шарфів — 15 мотків, 1 шарф — однаково
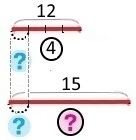
План розв’язування
1) Скільки мотків потрібно на 1 шарф? 12 : 4 = 3 (м.)
2) Скільки таких шарфів можна сплести з 15 мотків шерсті? 15 : 3 = 5 (ш.)
Розв’язання
15 : (12 : 4) = 5 (ш.)
Відповідь: можна сплести 5 шарфів.
Завдання 362 Задача на зведення до одиниці
За 5 однакових блокнотів заплатили 15 грн. Скільки таких блокнотів можна купити на 24 грн?
Короткий запис
5 блокнотів — 15 грн, 1 блокнот — ? грн
? блокнотів — 24 грн, 1 блокнот — однаково
План розв’язання
1) Яка ціна блокнота?
2) Скільки таких блокнотів можна купити на 24 грн?
Розв’язання
1) 15 : 5 = 3 (грн) – ціна блокнота.
2) 24 : 3 = 8 (бл.) – таких блокнотів можна купити.
Відповідь: можна купити 8 таких блокнотів.
Завдання 363 У Оленки на 12 значків більше, ніж в Олега, а в Олега їх у 4 рази менше, ніж в Оленки. Скільки значків у Олега?
Міркуємо так. Якщо в Олега значків у 4 рази менше, тоді в Оленки їх у 4 рази більше, що означає в Олега 1 частина значків, а в Оленки 4 таких частин. А їх різниця 3 частини дорівнює 12 значків, тому
12 : 3 = 4 (зн.) – значків у Олега (1 частина значків).
Відповідь: в Олега 4 значки.
Завдання 364
23 : 4 = 5 (ост. 3) 38 : 6 = 6 (ост. 2) 44 : 5 = 8 (ост. 4) 41 : 7 = 5 (ост. 6)
Завдання 365 Складена задача на віднімання
У квітковий кіоск завезли 120 тюльпанів. До обіду продали 7 букетів по 5 тюльпанів і один букет з 15 тюльпанів. Скільки тюльпанів залишилося в кіоску?
|
Було |
Продали |
Залишилося |
|
120 тюльпанів |
7 букетів по 5 тюльпанів і 15 тюльпанів |
? |
Короткий запис
Було — 120 тюльпанів
Продали — ?, (? т., 7 букетів по 5 тюльпанів) і 15 тюльпанів
Залишилося — ?
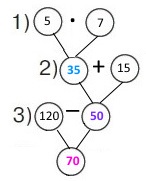
Вираз 120 – (5 • 7 + 15)
План розв’язування
1) Скільки тюльпанів у всіх букетах?
2) Скільки всього тюльпанів продали?
3) Скільки тюльпанів залишилося в кіоску?
Розв’язання
1) 5 • 7 = 35 (т.) – тюльпанів у всіх букетах.
2) 35 + 15 = 40 + 10 = 50 (т.) – всього тюльпанів продали.
3) 120 – 50 = 120 – 100 + 50 = 70 (т.) – тюльпанів залишилося в кіоску.
Відповідь: у кіоску залишилося 70 тюльпанів.