Інші завдання дивись тут...

© Барна Р., 2020

Серія "Вчимось разом" до підручника 

"Математика 3 клас Скворцова С., Онопрієнко О. (частина 2)"

Сторінка 46

Завдання 7  Додавання і віднімання частинами

Завдання 8 Множення і ділення способом укрупнення розрядів

Завдання 9  Задача на зведення до одиниці

За 4 год роботи генератор витратив 36 л бензину, витрачаючи щогодини однакову кількість літрів. Скільки літрів бензину по­трібно генератору на 6 год роботи?

^{1 спосіб (арифметичний)}

^{Короткий запис}

^{4 год — 36 л}

^{6 год — ? л}

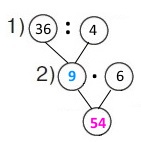
^{Вираз    36 : 4 • 6}

Розв'язання

1) 36 : 4 = 9 (л) – літрів витрачає за 1 год.

2) 9 • 6 = 54 (л) – літрів бензину потрібно на 6 год.

_{2 спосіб (алгебраїчний, тобто рівнянням)}

Нехай а (л) – літрів бензину потрібно на 6 год, тоді а : 6 (л) – щогодинна витрата, також 36 : 4 (л) – щогодинна витрата. Складемо рівняння:

а : 6 = 36 : 4

а : 6 = 9

а = 9 • 6

а = 54 (л)

Відповідь: генератору потрібно 54 літри бензину.

Завдання 10  У двох коробках по 20 цукерок. Ласунка Майя з'ї­ла кілька цукерок із першої коробки. Побачивши це, ласунка Олена з'їла з другої коробки стільки цукерок, скільки залишилося в першій. Скільки всього цукерок залишилося в обох коробках?

1 спосіб (табличний)

20 – х + х = 20 (ц.)

2 спосіб

^{Короткий запис}

^{Було — 20 цукерок і 20 цукерок}

^{З’їли — х цукерок  і (20 – х) цукерок}

^{Залишилось — ?}

Нехай х (ц.) – цукерок з'їла Майя, тоді 20 – х (ц.) – цукерок залишилося в першій коробці, тобто з’їла Оленка. Від цукерок, що були, віднімемо цукерки, що з'їли дівчата, тоді

(20 + 20) – х – (20 – х) = 40 – х – 20 + х = 20 (ц.)

Відповідь: у двох коробках залишилося 20 цукерок.

Сторінка 47

Завдання 1

_{1) Складена задача на множення}

У їдальню привезли 6 ящиків абрикосів і 8 таких ящиків персиків. Загальна маса абрикосів  42 кг. Скільки кілограмів персиків привезли, якщо маса одного ящика однакова?

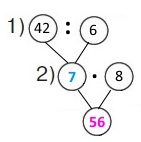
^{Вираз         42 : 6 • 8}

Розв'язання

1) 42 : 6 = 7 (кг) – маса 1 ящика з абрикосами (персиками).

2) 7 • 8 = 56 (кг)– кілограмів персиків привезли.

Відповідь: привезли 56 кілограмів персиків.

_{2) Складена задача на ділення}

У їдальню привезли 6 однакових ящиків абрикосів, по 4 кг у кожному ящику, і 8 ящиків персиків. Яка маса одного ящика персиків, якщо загальна маса персиків і абрикосів однакова?

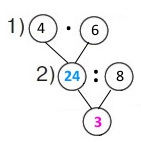
^{Вираз        4 • 6 : 8}

Розв'язання

1) 4 • 6 = 24 (кг) – загальна маса абрикосів (персиків).

2) 24 : 8 = 3 (кг) – маса ящика персиків.  

Відповідь: маса одного ящика персиків 3 кілограми.

Сторінка 48

_{Перша обернена задача на знаходження числа 8  (4, 6, 3, ?)}

У їдальню привезли 6 однакових ящиків абрикосів, по 4 кг у кожному ящику, і декілька ящиків персиків, по 3 кг у кожному. Скільки ящиків із персиками привезли в їдальню?

Розв'язання

1) 4 • 6 = 24 (кг) – загальна маса абрикосів (персиків).

2) 24 : 3 = 8 (ящ.) – ящиків із персиками привезли.

Відповідь: у їдальню привезли 8 ящиків із персиками.

_{Друга обернена задача на знаходження числа 6  (4, ?, 3, 8)}

У їдальню привезли 8 однакових ящиків персиків, по 3 кг у кожному ящику, і декілька ящиків абрикосів, по 4 кг у кожному. Скільки ящиків із абрикосами привезли в їдальню?

Розв'язання

1) 3 • 8 = 24 (кг) – загальна маса абрикосів (персиків).

2) 24 : 4 = 6 (ящ.)– ящиків з абрикосами привезли.  

Відповідь: привезли 6 ящиків із абрикосами.

_{Третя обернена задача на знаходження числа 4 (?, 6, 3, 8)}

У їдальню привезли 8 однакових ящиків персиків, по 3 кг у кожному ящику, і 6 ящиків абрикосів. Яка маса одного ящика абрикосів, якщо загальна маса персиків і абрикосів однакова?

Розв'язання

1) 3 • 8 = 24 (кг) – загальна маса абрикосів (персиків).

2) 24 : 6 = 4 (кг) – маса ящика абрикосів.

Відповідь: маса ящика абрикосів 4 кілограми.

Завдання 2  Додавання і віднімання частинами

560 + 250 = 560 + 40 + 210 = 600 + 210 = 810

220 – 150 = 220 – 120 – 30 = 100 – 30 = 70

170 + 340 = 170 + 30 + 310 = 200 + 310 = 510

420 – 380 = 420 – 320 – 60 = 100 – 60 = 40

370 + 250 = 370 + 30 + 220 = 400 + 220 = 620

900 – 430 = 900 – 400 – 30 = 500 – 30 = 470

430 + 180 = 430 + 70 + 110 = 500 + 110 = 610

880 – 490 = 380 + (500 – 490) = 380 + 10 = 390

270 + 270 = 270 + 30 + 240 = 300 + 240 = 540

740 – 660 = 40 + (700 – 660) = 40 + 40 = 80

630 + 290 = 630 + 70 + 220 = 700 + 220 = 920

710 – 520 = 110 + (600 – 520) = 110 + 80 = 190

Завдання 3  У двох коробках 22 олівці. У першій коробці на 2 олівці більше, ніж у дру­гій. Скільки олівців у кожній коробці?

Розв'язання

1 спосіб (арифметичний)

1) 22 – 2 = 20 (ол.) – олівців у двох коробках порівну.

2) 20 : 2 = 10 (ол.) – олівців у другій коробці.

3) 10 + 2 = 12 (ол.) – олівців у першій коробці.

^{2 спосіб (алгебраїчний)}

^{Нехай х (ол.) – олівців у другій коробці, тоді х + 2 (ол.) – олівців у першій коробці. Складемо рівняння}

^{(х + 2) + х = 22}

^{х + 2 + х = 22}

^{х • 2 + 2 = 22}

^{х • 2 = 22 – 2}

^{х • 2 = 20}

^{х = 20 : 2}

^{х = 10 (ол.) – у другій коробці}

^{х + 2 = 10 + 2 = 12 (ол.) – у першій коробці}

Відповідь: у першій коробці 12 олівців, у другій – 10 олівців.

Інші завдання дивись тут...