© Барна Р., 2020
Серія "Вчимось разом" до підручника "Математика 3 клас Заїка А., Тарнавська С."
Завдання 118 Переставний закон множення
2 • 5 = 5 • 2 = 10 5 • 3 • 2 = 5 • 2 • 3 = 10 • 3 = 30
Завдання 119
7 • 10 = 10 • 7 7 • 5 • 2 = 5 • 2 • 7
Завдання 120
Числові рівності: 200 • 3 = 3 • 200 40 • 5 = 4 • 50 10 • 2 = 2 • 10 100 • 8 = 8 • 100
Завдання 121
4 • 3 • 5 = (4 • 3) • 5 = 12 • 5 = 60 (добуток суми і числа)
4 • 3 • 5 = 4 • (3 • 5) = 4 • 15 = 60 (добуток числа і суми)
Завдання 122
|
4 • 3 • 5 = (4 • 3) • 5 = 4 • (3 • 5) |
||
|
добуток трьох чисел 3, 4 і 5 |
добутку перших двох чисел 4 і 3, помноженому на третє число 5 |
першому числу 4, помноженому на добуток двох інших чисел 3 і 5. |
Сполучний закон множення: а • b • с = (а • b) • с = а • (b • с)
Завдання 123
10 • 4 • 3 = 10 • 12 = 120 3 • 4 • 10 = 12 • 10 = 120
100 • 2 • 2 = 100 • 4 = 400 2 • 3 • 100 = 6 • 100 = 600
Завдання 124
3 • 4 = 12 (см) – периметр квадрата ABON зі стороною 3 см.
3 • 4 = 12 (см) – периметр квадрата CDNO зі стороною 3 см.
3 • 2 + (3 + 3) • 2 = (3 + 3 + 3) • 2 = 9 • 2 = 18 (см) – периметр прямокутника ABCD довжиною 6 см і шириною 3 см.
Оскільки прямокутник ABCD складається з двох квадратів, тому периметр можна знайти способом 3 • 6 = 18 (см)
Завдання 125 Порядок дій
|
(120 + 180) • 3 = 300 • 3 = 900 1) 120 + 180 = 200 + 100 = 300 2) 300 • 3 = 900 (140 – 40) • 4 = 100 • 4 = 400 1) 140 – 40 = 100 2) 100 • 4 = 400 (920 – 20) : 9 = 900 : 9 = 100 1) 920 – 20 = 900 2) 900 : 9 = 100 |
(370 + 130) : 5 = 500 : 5 = 100 1) 370 + 130 = 400 + 100 = 500 2) 500 : 5 = 100 64 – 4 • 7 – 13 = 64 – 28 – 13 = 23 1) 4 • 7 = 28 2) 64 – 28 = 64 – 30 + 2 = 34 + 2 = 36 3) 36 – 13 = 23 28 + 5 • 7 – 38 = 28 + 35 – 38 = 25 1) 5 • 7 = 35 2) 28 + 35 = 28 + 2 + 33 = 63 3) 63 – 38 = 63 – 40 + 2 = 23 + 2 = 25 |
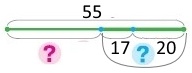
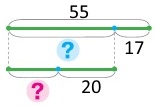
Завдання 126 Складена задача на віднімання суми від числа
Оля виконала домашнє завдання за 55 хв. Завдання з математики виконувала 17 хв, з української мови — 20 хв, решту часу читала. Скільки хвилин читала Оля?
|
1 спосіб Короткий запис Було — 55 хв Виконувала — ?, 17 хв і 20 хв Залишилось (решта) — ?
Вираз 55 – (17 + 20) План розв’язування 1) Скільки всього хвилин виконувала домашнє завдання? 2) Скільки хвилин читала Оля? Розв'язання 1) 17 + 20 = 37 (хв) – всього хвилин виконувала домашнє завдання. 2) 55 – 37 = 55 – 40 + 3 = 18 (хв) – хвилин читала Оля. Відповідь: Оля читала 18 хвилин. |
2 спосіб Оскільки Оля спочатку виконувала завдання з математики, а потім з української мови, тоді Короткий запис Було — 55 хв Виконувала математику — 17 хв Залишились (Було) — ? Виконувала мову — 20 хв Залишилось (решта) — ?
Вираз (55 – 17) – 20 План розв’язування 1) Скільки хвилин залишилося на мову і читання? 2) Скільки хвилин читала Оля? Розв'язання 1) 55 – 17 = 55 – 20 + 3 = 38 (хв) – хвилин залишилося на мову і читання. 2) 38 – 20 = 18 (хв) – хвилин читала Оля. Відповідь: Оля читала 18 хвилин. |
Завдання 127 Обчислили, використовуючи переставний і сполучний закони множення
Значення добутку кількох множників не зміниться, якщо їх переставити місцями і взяти в дужки (сполучити) ті множники, що стоять поруч.
25 • 5 • 4 = 25 • 4 • 5 = 100 • 5 = 500
2 • 7 • 5 = 7 • 2 • 5 = 7 • 10 = 70
25 • 25 • 4 • 4 = 25 • 4 • 25 • 4 = 100 • 100 = 10000
50 • З • 2 = 50 • 2 • 3 = 100 • 3 = 300
Завдання 128 Рівняння
|
Множення |
Віднімання |
Додавання |
Ділення |
|
х • 30 = 60 х = 60 : 30 х = 2 2 • 30 = 60 60 = 60 |
х – 170 = 340 х = 340 + 170 х = 510 510 – 170 = 340 340 = 340 |
х + 170 = 340 х = 340 – 170 х = 170 170 + 170 = 340 340 = 340 |
у : 5 = 8 у = 8 • 5 у = 40 40 : 5 = 8 8 = 8 |
|
8 • у = 64 у = 64 : 4 у = 8 8 • 8 = 64 64 = 64 |
х – 7 = 42 х = 42 + 7 х = 49 49 – 7 = 42 42 = 42 |
|
х : 10 = 30 х = 30 • 10 х = 300 300 : 10 = 30 30 = 30 |
|
х • 7 = 42 х = 42 : 7 х = 6 6 • 7 = 42 42 = 42 |
|
|
|
Завдання 129
Якщо одиницю помножити на деяке число, тоді отримаємо те саме число.
1 • а = а, де а — будь–яке число 1 • 5 = 5 1 • 9 = 9
Якщо нуль помножити на деяке число, тоді отримаємо нуль.
0 • а = 0, де а — будь–яке число 0 • 5 = 0 0 • 9 = 0
Завдання 130
|
1 • 120 = 120 1 • 350 = 350 170 • 1 = 170 |
0 • 700 = 0 0 • 732 = 0 316 • 0 = 0 |
(824 – 823) • 823 = 1 • 823 = 823 (824 – 824) • 824 = 0 • 824 = 0 42 • (130 – 130) = 42 • 0 = 0 |
Завдання 131
Якщо будь-яке число помножити на одиницю, тоді отримаємо те саме число: а • 1 = а
Якщо будь-яке число помножити на нуль, тоді отримаємо нуль: а • 0 = 0
Завдання 132 Підкреслили однакові результати, серед інших — виділили найбільший:
73 • 1 = 73 374 • 1 = 374 255 • 0 = 0 847 • 0 = 0
173 • 1 = 173 1000 • 1 = 1000 107 • 0 = 0 1000 • 0 = 0
Завдання 133
а) добуток чисел а і З0 збільшити на 50:
якщо а = 0, тоді (а • 30) + 50 = (0 • 30) + 50 = 0 + 50 = 50
б) частку від ділення а на 10 помножити на 1000:
якщо а = 0, тоді (а : 10) • 1000 = (0 : 10) • 1000 = 0 • 1000 = 0
Завдання 134 Складена задача на різницеве порівняння
Гелікоптер першого дня пролетів 600 км, а другого — в а разів менше На скільки кілометрів менше гелікоптер пролетів другого дня, ніж першого?
Короткий запис
І день — 600 км
ІІ день — ?, в а разів менше; на ? км менше
Вираз 600 – 600 : а
1) 600 : а (км) – відстань другого дня.
2) 600 – 600 : а (км) – на стільки кілометрів менше гелікоптер пролетів другого дня, ніж першого.
Якщо а = 2, тоді 600 – 600 : а = 600 – 600 : 2 = 600 – 300 = 300 (км)
Якщо а = 3, тоді 600 – 600 : 3 = 600 – 600 : 3 = 600 – 200 = 400 (км)
Завдання 135 Складена задача на зменшення на деяке число
За 2 передноворічні дні магазин продав 400 тортів. Скільки тортів було продано в наступні 2 післяноворічні дні, якщо щоденний продаж зменшився на 100 тортів?
1 спосіб
Короткий запис
Передноворічні — 400 тортів
Післяноворічні — ?, на (? т., 2 дні по 100 тортів) менше
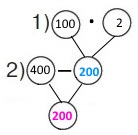
Вираз 400 – 100 • 2
План розв’язування
1) На скільки зменшився продаж за два післяноворічних дні?
2) Скільки тортів було продано в наступні два післяноворічні дні?
Розв’язання
1) 100 • 2 = 200 (т.) – на стільки тортів зменшився продаж за два післяноворічні дні.
2) 400 – 200 = 200 (т.) – тортів було продано в наступні два післяноворічні дні.
2 спосіб
|
Дні |
Тортів за день |
Кількість днів |
Загальна кількість тортів |
|
Передноворічні |
? |
2 |
400 |
|
Післяноворічні |
?, на 100 тортів менше |
2 |
? |
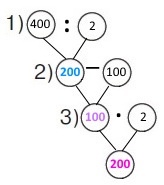
Вираз (400 : 2 – 100) • 2
План розв’язування
1) Скільки тортів було продано щоденно в передноворічні дні?
2) Скільки тортів було продано щоденно в післяноворічні дні?
3) Скільки тортів було продано в наступні два післяноворічні дні?
Розв’язання
1) 400 : 2 = 200 (т.) – тортів продав щоденно в передноворічні дні.
2) 200 – 100 = 100 (т.) – щоденний продаж в післяноворічні дні.
3) 100 • 2 = 200 (т.) – тортів було продано в наступні два післяноворічні дні.
Відповідь: у наступні два післяноворічні дня магазин продав 200 тортів.
Завдання 136 Дії з іменованими числами
|
289 м + 1 м = 290 м 500 кг – 310 кг = 500 кг – 300 кг – 10 кг = 190 кг 8 кг • 3 = 24 кг 42 см : 7 = 6 см |
810 грн – 340 грн = 810 грн – 310 грн – 30 грн = 470 грн 17 км + 34 км = 51 км 10 грн • 10 = 100 грн 56 л : 8 = 7 л |
Завдання 137
|
1 • 10 + 1 • 150 = 10 + 150 = 160 0 • 48 + 1 • 100 = 0 + 100 = 100 |
(40 + 50) • 0 = 90 • 0 = 0 1 • (20 • 4) = 1 • 80 = 80 |
64 : 8 + 32 : 4 = 8 + 8 = 16 81 : 9 – 72 : 9 = 9 – 8 = 1 |
Якщо один із множників дорівнює нулю, тоді добуток дорівнює нулю:
3 • 5 • 7 • 0 • 8 • 9 • 1 • 2 • 4 • 6 • 10 = 0
Завдання 138 Складена задача на збільшення на деяке число і знаходження суми
Туристи першого дня пройшли 16 км, наступного — на а км більше. Скільки кілометрів пройшли туристи за 2 дні?
Короткий запис
І день — 16 км
ІІ день — ?, на а км більше
Всього — ?
Вираз 16 + (16 + а)
1) 16 + а (км) – відстань пройшли другого дня.
2) 16 + (16 + а) (км) – кілометрів пройшли туристи за два дні.
Якщо а = 4, тоді 16 + (16 + а) = 16 + (16 + 4) = 16 + 20 = 36
Якщо а = 5, тоді 16 + (16 + а) = 16 + (16 + 5) = 16 + 21 = 37
Завдання 139
|
а • b • 0 = (а • b) • 0 = 0 |
а • b • 1 = (а • b) • 1 = а • b |
(m + n) • 1 = m + n |