Інші завдання дивись тут...

Завдання 151 Яку частину становить:

1 м від 1 км =1 м : 1 км = 1 м : 1000 м = 1/1000

1 місяць від 1 року =  1 міс. : 1 рік = 1 міс. : 12 міс = 1/12

1 хв від 1 год = 1 хв : 1 год = 1 хв : 60 хв = 1/60

1 год від 1 доби = 1 год : 1 доба = 1 год : 24 год = 1/24

1 кг від 1 ц = 1 кг : 1 ц = 1 кг : 100 кг = 1/100

1 кг від 1 т = 1 кг : 1 т = 1 кг : 1000 кг = 1/1000

1 ц від 1 т = 1 ц : 1 т = 1 ц : 10 ц = 1/10

1 г від 1 кг = 1 г : 1 кг =  1 г : 1000 г = 1/1000 

 

Завдання 152 Письмове множення і письмове ділення

Два автомобілі одночасно виїхали в одному напрямку з одного пункту. Швидкість першо­го автомобіля становила 70 км/год, а швид­кість другого — 85 км/год. Яка відстань буде між ними через 2 год?

Схематичний рисунок

—> v2 = 85 км/год         —> v1 = 70 км/год         t = 2 год       ∆—————————————∆—————————————|                                    S — ? км

Розв'язання

1–й спосіб

1) 70 • 2 = 140 (км) – пройшов I автомобіль за 2 год;

2) 85 • 2 = 170 (км) – пройшов II автомобіль за 2 год.

3) 170 – 140 = 30 (км)

2–й спосіб

1) 85 – 70 = 15 (км) – відстань, на яку зближаються за 1 год;

2) 15 • 2 = 30 (км) – відстань, на яку зближаються за 2 год.

Відповідь: між автомобілями буде 30 км через 2 години.

 

Завдання 154

У змаганнях з дитячого любительського картингу одна машина зі старту набрала швидкість 18 км/год, а друга — 24 км/год. Яка відстань буде між ними через 5 хв с після одночасного старту? Розв'яжи двома способами.

Розв'язання

18 км/год = 18000 м : 60 хв = 300 м/хв, 24 км/год = 24000 м : 60 хв = 400 м/хв

1–й спосіб

1) 300 • 5 = 1500 (м) – відстань пройшла I машина за 5 хв;

2) 400 • 5 = 2000 (м) – відстань пройшла II машина за 5 хв.

3) 2000 + 1500 = 500 (м)

2–й спосіб

1) 400 – 300 = 100 (м) – відстань між ними за 1 хв;

2) 100 • 5 = 500 (м) – відстань між ними за 5 хв.

Відповідь: між ними буде 500 метрів через 5 хв.

 

Завдання 155

1) З двох населених пунктів одночасно назустріч один одному виїхали два велосипедисти. Швидкість першого велосипедиста 16 км/год, а швидкість другого — 11 км/год. Яка відстань буде між велосипедистами через 2 год?

Схематичний рисунок

16 км/год —>                          t = 2 год                <— 11 км/год        |——————————————∆———————————|                                            S – ?

Розв'язання

1) 16 + 11 = 27 (км) – відстань, на яку наближаються через 1 год;

2) 27 • 2 = 54 (км) – відстань, на яку наближаються через 2 год.

Відповідь: між велосипедистами буде 54 км через 2 години.

2) З одного населеного пункту одночасно в протилежних напрямках виїхали два автомобілі. Через 3 год відстань між ними була 420 км. Якою була швидкість другого автомобіля, якщо швидкість першого автомобіля 60 км/год?

Схематичний рисунок

t = 3 год                                 60 км/год <—     —> ? км/год        |——————————————∆———————————|                                           S – 420 км

Розв'язання

1) 60 • 3 = 180 (км) – відстань проїхав I автомобіль;

2) 420 – 180 = 240 (км) – відстань проїхав II автомобіль.

3) 240 : 3 = 80 (км/год)

Відповідь: швидкість другого автомобіля 80 км/год.

 

Завдання 156 Дії з іменованими величинами

Екскурсія містом триває 3 год 20 хв. Початок екскурсій о 8 год 10 хв, о 12 год, о 16 год. На які екскурсії може піти турист, якщо йому треба встигнути на поїзд, який від'їжджає о 18 год?

Короткий запис

Початок — 8 год 10 хв, о 12 год, о 16 год

Триває — 3 год 20 хв

Закінчується — 18 год

Розв'язання

18 год – 3 год 20 хв = 17 год 60 хв – 3 год 20 хв = 14 год 40 хв

8 год 10 хв < 14 год 40 хв; 12 год < 14 год 40 хв

Відповідь: турист може піти на екскурсії о 8 год 10 хв і о 12 год.

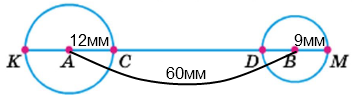
Довжина відрізка AB дорівнює 6 см. Радіус кола із центром у точці A дорівнює 1 см 2 мм, а із центром у точці B — 9 мм. Знайди відста­ні KM і CD. (Результати обчислень перевір вимірюванням.

АВ = 6 см = 60 мм, KA = AC = 1 см 2 мм = 12 мм, DB = BM = 9 мм

Розв'язання
CD = AB – AC – DB = 60 мм – 12 мм – 9 мм = 39 мм = 3 см 9 мм
KM = KA + AB + BM = 12 мм + 60 мм + 9 мм = 81 мм = 8 см 1 мм

Завдання 158

Тарас купив 10 зошитів, а Юрко — 8. До них приєднався Олесь, і вони поділили всі зошити порівну. Олесь повернув їм за зошити 36 грн. Скільки грошей із цієї суми одержить Тарас і скільки — Юрко?

Розв'язання
1) 10 + 8 = 18 (з.) – купили  Тарас і Юрко;
2) 18 : 3 = 6 (з.) – отримав кожен з хлопців;

3) 36 : 6 = 6 (грн) – ціна зошита;
4) 10 – 6 = 4 (з.) – віддав Тарас;
5) 8 – 6 = 2 (з.) – віддав Юрко;
6) 4 • 6 = 24 (грн) – грошей одержить Тарас;
7) 2 • 6 = 12 (грн) – грошей одержить Юрко.
Відповідь: Тарас одержить 24 грн, а Юрко одержить 12 грн.

 

Завдання 159

Із селища Л до селища С одночасно виїхали скутерист та велосипедист. Швидкість скутериста становила 30 км/год, а швидкість велосипедиста була меншою від швидкості скуте­риста на 16 км/год. Якою буде відстань між ними через 3 год після початку руху?

Схематичний рисунок

—> v1 = ?, на 16 км/год менше        —> v2 = 30 км/год                     t = 2 год        ∆—————————————∆—————————————|                                    S — ? км

Розв'язання

1–ий спосіб

1) 30 – 16 = 14 (км/год) – швидкість велосипедиста;
2) 14 • 3 = 42 (км) – відстань проїхав велосипедист;

3) 30 • 3 = 90 (км) – відстань проїхав скутерист.
4) 90 – 42 = 48 (км)

2–ий спосіб

1) 30 – 16 = 14 (км/год) – швидкість велосипедиста;
2) 30 – 14 = 16 (км) – відстань між ними за 1 год;

3) 16 • 3 = 48 (км) – відстань між ними за 3 год.

Відповідь: між ними буде 48 км через 3 год після початку руху.

 

Завдання 160 Письмове множення і письмове ділення

1) Добуток чисел 8 і 9 зменшити на частку чисел 63 і 7.

8 • 9 – 63 : 7 = 72 – 9 = 63

2) Різниця добутку чисел 7 і 9 та добутку чисел 6 і 8.

7 • 9 – 6 • 8 = 63 – 48 = 15

3) Добуток чисел 6 і 9 збільшити на частку чисел 32 і 4.

6 • 9 + 32 : 4 = 54 + 8 = 62

 

Завдання 162

За який час легковий автомобіль наздожене вантажний, якщо відстань між ними стано­вить 36 км, а швидкість легкового автомобіля більша від швидкості вантажного на 12 км?

Схематичний рисунок

—> v1 = ?, на 12 км/год менше        —> v2 – ?                                t – ? год        ∆—————————————∆—————————————|                                    S — 36 км

Розв'язання

36 : 12 = 3 (год)

Відповідь: за 3 год легковий автомобіль наздожене вантажний.

 

Завдання 163

 До Червоної книги занесені тигрова акула і велика біла акула.

 

Завдання 164

Із двох великих міст назустріч один одному вийшли два пасажирських потяги. Один із них пройшов до зустрічі 178 км, а другий — у 2 рази більше. Чому дорівнює відстань між містами?

Схематичний рисунок

S1 178 км —>                                            <— S2 у 2 рази більше        |——————————————∆———————————|                                            S – ?

Розв'язання

1) 178 • 2 = 356 (км) – відстань пройшов другий потяг.
2) 178 + 356 = 534 (км)

Відповідь: між містами буде 534 км.

 

Завдання 165

Побудуй лінійну або стовпчасту діаграму най­більших мас тварин. Побудуй лінійну або стовпчасту діаграму найбільших мас тварин. Склади задачі за цими даними. Маса африканського слона — 7500 кг, індійського слона — 4000 кг, бегемота — 4000 кг, носорога — 2000 кг.

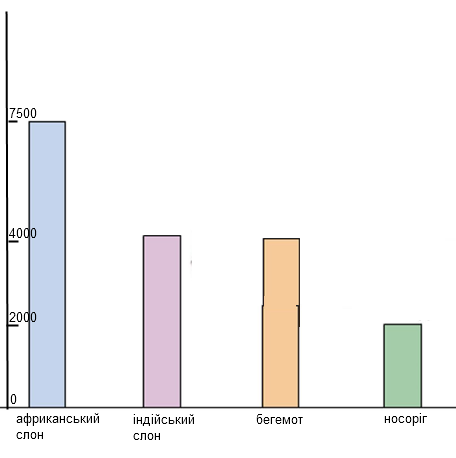
На скільки кілограмів маса африканського слона більша, ніж індійського слона?

Які тварини мають однакову масу?
У скільки разів носоріг легший від бегемота?

 

Завдання 166

Супермаркет зачиняється о 23 год 15 хв. Чи встигне покупець здійснити покупки, якщо о 22 год 20 хв він вийшов до супермаркету, на дорогу до якого йому потрібно витратити 25 хв, а для здійснення покупок — 20 хв?

Розв'язання
22 год 20 хв + 25 хв + 20 хв = 22 год 65 хв = 23 год 5 хв

Відповідь: покупець встигне здійснити покупки.

 

Завдання 167 Порядок дій

Довжина баскетбольного майданчика 26 м, а його ширина — на 12 м менша. Обчисли периметр та площу цього майданчика.

^{Короткий запис}

^{Довжина — 26 м}

^{Ширина — ?, на 12 м менша}

^{Периметр — ?}

^{Площа — ?}

Розв'язання
1) 26 – 12 = 14 (м) – ширина майданчика;
2) (26 + 14) • 2 = 40 • 2 = 80 (м) – периметр майданчика;

3) 26 • 14 = 364 (м²) – площа майданчика.
Відповідь: периметр майданчика 80 м, площа майданчика 364 м².

Побудуй план майданчика з масштабом: в 1 см — 4 м.

Треба побудувати прямокутник довжиною 6 см 5 мм і шириною 3 см 5 мм.

 

Завдання 169

а) запиши число 100 п'ятьма одиницями і зна­ками дій;

111 – 11 = 100

б) запиши число 100 п'ятьма трійками.

33 • 3 + 3 : 3 = 100

 

Завдання 170

Відстань від зупинки A до зупинки B міська електричка подолала за 3/4 год. 1/6 год вона витратила на зупинки. Скільки хвилин руха­лась електричка від зупинки A до зупинки B?

^{Короткий запис}

^{АВ — 3/4 год}

^{Зупинки — ?, 1/6 год}

^{Час — ?}

Розв'язання

1 год = 60 хв
1) 60 : 4 • 3 = 15 • 3 = 45 (хв) – час в дорозі;

2) 60 : 6 • 1 = 10 (хв)  – час зупинок.

3) 45 + 10 = 55 (хв)
Відповідь: електричка рухалася 55 хв.

 

Завдання 171 Дії з іменованими величинами

Інші завдання дивись тут...