CТОРІНКА 29
46 : 5 = 9 (ост. 1)
31 : 5 = 6 (ост. 1)
18 : 7 = 2 (ост. 4)
22 : 7 = 3 (ост. 1)
28 : 9 = 3 (ост. 1)
|
9 • 5 + 1 = 46
6 • 5 + 1 = 31
2 • 7 + 4 = 18
3 • 7 + 1 = 22
9 • 3 + 1 = 28
|
30 : 9 = 3 (ост. 3)
38 : 4 = 9 (ост. 2)
56 : 6 = 9 (ост. 2)
50 : 7 = 7 (ост. 1)
18 : 4 = 4 (ост. 2)
|
3 • 9 + 3 = 30
9 • 4 + 2 = 38
9 • 6 + 2 = 56
7 • 7 + 1 = 50
4 • 4 + 2 = 18
|
|
|
|
|
_9225 | 3
9 3075
_22
21
_15
15
0
|
_15460 | 5
15 3092
_46
45
_10
10
0
|
_926424 | 9
9 102936
_26
18
_84
81
_32
27
_54
54
0
|
|
|
|
х 95
4
380
|
х 3075
3
9225
|
х 3092
5
15460
|
х 102936
9
926424
|
|
Письмове ділення
|
|
_30360 | 5
30 6072
_36
35
_10
10
0
|
_40160 | 5
40 8032
_16
15
_10
10
0
|
_12180 | 4
12 3045
_18
16
_20
20
0
|
_145006 | 2
14 72503
_5
4
_10
10
_6
6
0
|
|
Перевірка письмовим множенням
|
|
х 6072
5
30360
|
х 8032
5
40160
|
х 3045
4
12180
|
х 72503
2
145006
|
Завдання 4
Кравчиня придбала 8 м костюмної тканини, заплативши за неї 2456 грн. Стільки само вона купила підкладкової тканини, 1 м якої коштує на 200 грн менше, ніж костюмної. Скільки грошей заплатила кравчиня за всю тканину?
|
|
|
|
|
|
|
|
|
|
|
| Підкладкова |
?, на 200 грн менше |
8 м |
? |
1) 2456 : 8 = 307 (грн) – ціна 1 м костюмної тканини;
2) 307 – 200 = 107 (грн) – ціна 1 м підкладкової тканини;
3) 107 • 8 = 856 (грн) – вартість підкладкової тканини;
4) 2456 + 856 = 3312 (грн) – вартість тканини.
ІІ спосіб
1) 200 • 8 = 1600 (грн) – різниця між вартістю костюмної тканини і підкладкової;
2) 2456 – 1600 = 856 (грн) – вартість підкладкової тканини;
3) 2456 + 856 = 3312 (грн) – вартість тканини.
_51856 | 7
49 7408
_28
28
_56
56
0
|
_73608 | 8
72 9201
_16
16
_8
8
0
|
_77161 | 7
7 11023
_7
7
_16
14
_21
21
0
|
_548236 | 4
4 137059
_14
12
_28
28
_23
20
_36
36
0
|
|
|
_8150 | 2
8 4075
_15
14
_10
10
0
|
_21258 | 3
21 7086
_25
24
_18
18
0
|
_9252 | 3
9 3084
_25
24
_12
12
0
|
_8156 | 4
8 2039
_15
12
_36
36
0
|
|
|
_12376 | 4
12 3094
_37
36
_16
16
0
|
_18432 | 6
18 3072
_43
42
_12
12
0
|
_30260 | 5
30 6052
_26
25
_10
10
0
|
Скільки потрібно купюр по 50 грн, щоб сплатити 3150 грн за покупку?
Розв'язання
_3150 | 50
300 63 (к.)
_150
150
0
Відповідь: потрібно 63 купюри.
|
За малюнком і умовою розв’яжіть геометричну задачу. Відомо, що CBMN — квадрат. Довжина відрізка AN становить 16 см. Відрізок AC на чверть коротший від відрізка AN. Знайдіть периметри фігур CBMN і ADMN.
Розв'язання
1) 16 : 4 = 4 (см) – чверть відрізка AN;
2) 16 – 4 = 12 (см) – довжина відрізка AC;
3) 16 – 12 = 4 (cм) – довжина відрізка CN;
4) 4 • 4 = 16 (см) – периметр квадрата CBMN;
5) (16 + 4) • 2 = 40 (см) – периметр прямокутника ADMN.
Відповідь: периметр фігури CBMN 16 см і ADMN 40 см.
_1359 | 3
12 453
_15
15
_9
9
0
|
_6158 | 2
6 3079
_15
14
_18
18
0
|
_24380 | 4
24 6095
_38
36
_20
20
0
|
_27864 | 9
27 3096
_86
81
_54
54
0
|
|
|
|
|
|
|
|
CТОРІНКА 31
Завдання 1
Ніна купила 8 зошитів, а Максим — 4. Ніна заплатила на 20 грн більше, ніж Максим. Скільки заплатили Ніна і Максим за свої зошити окремо?
Короткий запис
Ніна — 8 з. — ?, на 20 грн більше
Максим — 4 з. — ?
Розв’язання
1) 8 – 4 = 4 (з.) – на стільки зошитів більше купила Ніна;
2) 20 : 4 = 5 (грн) – ціна зошита;
3) 5 • 4 = 20 (грн) – заплатив Максим;
4) 5 • 8 = 40 (грн) – заплатила Ніна.
Відповідь: Ніна заплатила 20 грн і Максим заплатив 40 грн.
Перевірка: 40 – 20 = 20 (грн)
Завдання 2
Садівник першого дня зібрав з дерев 8 однакових ящиків вишень, а другого дня — 12. Скільки кілограмів вишень зібрав садівник кожного дня окремо, якщо за другий день він зібрав на 20 кг вишень більше?
Короткий запис
I — 8 ящ. — ?
II — 12 ящ. — ?, на 20 кг більше
Розв’язання
1) 12 – 8 = 4 (ящ) – на стільки більше ящиків зібрав другого дня;
2) 20 : 4 = 5 (кг) – маса вишень в одному ящику;
3) 5 • 8 = 40 (кг) – зібрав першого дня;
4) 5 • 12 = 60 (кг) – зібрав другого дня.
Відповідь: садівник зібрав вишень 40 кг першого дня і 60 кг другого дня.
Завдання 3
Першого дня продали 18 однакових наплічників, другого — 15. За продаж наплічників першого дня одержали на 360 грн більше, ніж другого. Скільки грошей одержали за продаж наплічників кожного дня окремо?
Короткий запис
I — 18 н. — ?, на 360 грн більше
II — 15 н. — ?
Розв’язання
1) 18 – 15 = 3 (н.) – на стільки більше наплічників продали другого дня;
2) 360 : 3 = 120 (грн) – ціна одного наплічника;
3) 120 • 18 = 2160 (грн) – одержали грошей першого дня;
4) 120 • 15 = 1800 (грн) – одержали грошей другого дня.
Відповідь: одержали 2160 грн першого дня і 1800 грн другого дня.
СТОРІНКА 32
Завдання 4
На консервному заводі виготовили 40 банок вишневого соку і 50 таких самих банок виноградного соку, причому виноградного соку було на 30 л більше, ніж вишневого. Скільки літрів вишневого і виноградного соків виготовили окремо?
Короткий запис
Вишневий — 40 б. — ?
Виноградний — 50 б. — ?, на 30 л більше
Розв’язання
1) 50 – 40 = 10 (б.) – на стільки більше банок виноградного соку;
2) 30 : 10 = 3 (л) – місткість одної банки;
3) 3 • 40 = 120 (л) – виготовили вишневого соку;
4) 3 • 50 = 150 (л) – виготовили виноградного соку.
Відповідь: виготовили 120 л вишневого соку і 150 л виноградного соку.
Завдання 5
А. За коротким записом склади і розв’яжи задачу про масу банок із фарбою, використаних кожного дня окремо. Першого дня використали 20 банок фарби, а другого — 18 таких банок, причому першого дня використали на 6 кг більше фарби, ніж другого. Скільки фарби використали кожного дня окремо?
Короткий запис
I — 20 б. — ?, на 6 кг більше
II — 18 б. — ?
Розв’язання
1) 20 – 18 = 2 (б.) – на стільки більше банок використали першого дня;
2) 6 : 2 = 3 (кг) – маса одної банки;
3) 3 • 20 = 60 (кг) – використали фарби першого дня;
4) 3 • 18 = 54 (кг) – використали фарби другого дня.
Відповідь: фарби використали 60 кг першого дня і 54 кг другого дня.
Б. За таблицею склади задачу та розв’яжи її. Наталка пройшла 300 м, а Іван — 100 м, причому Наталка була в дорозі на 4 хв довше, ніж Іван. Скільки часу була в дорозі кожна дитина окремо, якщо вони рухалися з однаковою швидкістю?
Розв’язання
1) 300 – 100 = 200 (м) – на скільки більшу відстань пройшла Наталка;
2) 200 : 4 = 50 (м/хв) – швидкість кожної дитини;
3) 300 : 50 = 6 (хв) – була в дорозі Наталка;
4) 100 : 50 = 2 (хв) – був в дорозі Іван.
Відповідь: в дорозі була 6 хв Наталка і 2 хв Іван.
3720 – а > 2400
Розв'язуємо рівняння:
3720 – а = 2400
а = 3720 – 2400
а = 1320
Нерівність правильна, якщо а < 1320
а = 0, 1, 2, 3, 10, 100, 200
|
с • 9 < 63
Розв'язуємо рівняння:
с • 9 = 63
c = 63 : 9
c = 7
Нерівність правильна, якщо c < 7
с = 0, 1, 2, 3, 4, 5, 6
|
Розгляньте малюнок і визначте довжину відрізка СD, якщо КМ = 15 см.
Розв’язання
1) 3 + 2 = 5 (см) – довжина відрізків KC і DM разом;
2) 15 – 5 = 10 (см) – довжина відрізка CD.
Відповідь: 10 см.
Вираз: 15 – (3 + 2) = 10 (см)
Завдання 8
У касі крамниці монет по 5 грн стільки, скільки купюр по 10 грн. Скільки в касі гривень купюрами по 10 грн, якщо монетами по 5 грн — 800 грн?
Короткий запис
Монет по 5 грн — ? шт. — 800 грн
Купюр по 10 грн — ? шт., однаково — ? грн
Розв’язання
1) 800 : 5 = 160 (шт.) – монет по 5 грн або купюр по 10 грн.
2) 10 • 160 = 1600 (грн)
Відповідь: у касі 1600 гривень купюрами по 10 грн.
250 : 5 + 430 : 10 – 54 : 9 • 7 = 50 + 43 – 42 = 51
|
|
|
|
63 : 7 • 110 + (564 – 322) + 350 = 990 + 242 + 350 = 1582
|
|
|
+ 990
242
1232
|
+ 1232
350
1582
|
Завдання 10
Для пакування подарунків Ганна придбала 5 м стрічки, а Захар такої самої — 3 м. Скільки заплатили за свої стрічки Ганна і Захар окремо, якщо відомо, що Ганна заплатила на 20 грн більше?
Розв’язання
1) 5 – 3 = 2 (м) – на скільки більше стрічки придбала Ганна;
2) 20 : 2 = 10 (грн) – ціна одного метра стрічки;
3) 10 • 5 = 50 (грн) – грошей заплатила Ганна;
4) 10 • 3 = 30 (грн) – грошей заплатив Захар.
Відповідь: 50 грн заплатила Ганна і 30 грн заплатив Захар.
Обернена задача. За однакові стрічки для пакування подарунків Ганна заплатила 50 грн, а Захар — 30 грн. Скільки метрів стрічки придбали Ганна і Захар окремо, якщо відомо, що Ганна купила на 2 м довшу стрічку?
1) 50 – 30 = 20 (грн) – різниця вартості стрічок;
2) 20 : 2 = 10 (грн) – ціна одного метра стрічки;
3) 50 : 10 = 5 (м) – довжина стрічки, яку придбала Ганна;
4) 30 : 10 = 3 (м) – довжина стрічки, яку придбав Захар.
Відповідь: 5 м стрічки придбала Ганна і 3 м стрічки придбав Захар.
Завдання 11
Першого дня майстер працював 3 год, а другого — 5 год. Другого
дня він розмалював на 24 тарілки більше, ніж першого. Скільки тарілок розмалював майстер кожного дня окремо, якщо працював з однаковою продуктивністю?
Розв’язання
1) 5 – 3 = 2 (год) – на стільки більше працював другого дня;
2) 24 : 2 = 12 (т.) – розмальовує за одну год;
3) 12 • 3 = 36 (т.) – розмалював I дня;
4) 12 • 5 = 60 (т.) – розмалював II дня.
Відповідь: майстер розмалював 36 тарілок першого дня і 60 тарілок другого дня.
Обернена задача. Першого дня майстер розмалював 36 тарілок, а другого — 60 таких тарілок. Першого дня він працював на 2 год менше, ніж другого. Скільки годин працював майстер кожного дня окремо, якщо працював з однаковою продуктивністю?
1) 60 – 36 = 24 (т.) – різниця кількості тарілок;
2) 24 : 2 = 12 (т.) – розмальовує за одну год;
3) 36 : 12 = 3 (год) – працював I дня;
4) 60 : 12 = 5 (год) – працював II дня.
Відповідь: майстер працював 3 год першого дня і 5 год другого дня.
СТОРІНКА 34
Завдання 12
А. За короткими записами і схемою першої дії розв’яжи задачі про придбання зошитів дітьми. Максим купив 6 зошитів, а Олена — 4 таких зошитів, причому Максим заплатив за зошити на 18 грн більше, ніж Олена. Скільки грошей заплатила за зошити кожна дитина окремо?
Розв’язання
1) 6 – 4 = 2 (з.) – різниця кількості зошитів;
2) 18 : 2 = 9 (грн) – ціна одного зошита;
3) 9 • 6 = 54 (грн) – заплатив Максим;
4) 9 • 4 = 36 (грн) – заплатила Олена.
Відповідь: 54 грн заплатив Максим і 36 грн заплатила Олена.
Обернена задача. За однакові зошити Максим заплатив 54 грн, а Олена — 36 грн, причому Олена придбала на 2 зошити менше, ніж Максим. Скільки таких зошитів купила кожна дитина окремо?
1) 54 – 36 = 18 (грн) – різниця вартості зошитів;
2) 18 : 2 = 9 (грн) – ціна одного зошита;
3) 54 : 9 = 6 (з.) – купив Максим;
4) 36 : 9 = 4 (з.) – купила Олена.
Відповідь: 6 зошитів придбав Максим і 4 зошити придбала Олена.
Б. Вилучи зайві дані та розв’яжи задачу. За два дні велосипедист проїхав 46 км. До відпочинку він рухався 2 год, а після — 4 год. Скільки кілометрів проїхав велосипедист до відпочинку і після, рухаючись із однаковою швидкістю, якщо після відпочинку проїхав на 18 км більше, ніж до нього?
1) 4 – 2 = 2 (год) – різниця в часі руху;
2) 18 : 2 = 9 (км/год) – швидкість руху;
3) 9 • 2 = 18 (км) – відстань проїхав до відпочинку;
4) 9 • 4 = 36 (км) – відстань проїхав після відпочинку.
Відповідь: велосипедист проїхав 18 км до відпочинку і 36 км після відпочинку.
Обернена задача. До відпочинку велосипедист проїхав 18 км, а після — 36 км. Скільки годин він був в дорозі до відпочинку і після, рухаючись із однаковою швидкістю, якщо після відпочинку їхав на 2 год довше, ніж до нього?
1) 36 – 18 = 18 (км) – різниця відстані;
2) 18 : 2 = 9 (км/год) – швидкість руху;
3) 18 : 9 = 2 (год) – час в дорозі до відпочинку;
4) 36 : 9 = 4 (год) – час в дорозі після відпочинку.
Відповідь: велосипедист проїхав 2 год до відпочинку і 4 год після відпочинку.
Завдання 13
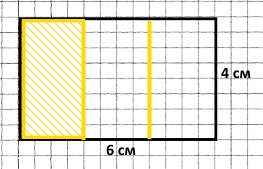
Накресліть прямокутник ABCD зі сторонами 6 і 4 см. Відокремте вертикальною лінією третю частину цього прямокутника і замалюйте.
6 : 3 = 2 (см) – припадає на 1/3 сторони довжиною 6 см.
7 т 56 кг > 756 кг (7 т 56 кг = 7056 кг)
3 м 40 см > 3 м 40 мм (40 см = 400 мм)
5 м 3 дм < 5 м 35 см (3 дм = 30 см)
|
803 ц > 8 т 3 ц (8 т 3 ц = 83 ц)
6054 см < 600 м 54 см (600 м 54 см = 60054 см)
46 км < 46 340 м (46 км = 46000 м)
|
Кравець придбав п’ять котушок білих ниток і три котушки чорних за однаковою ціною. Скільки заплатив кравець окремо за білі і чорні нитки, якщо за білі він заплатив на 40 грн більше, ніж за чорні?
1) 5 – 3 = 2 (н.) – різниця в кількості котушок;
2) 40 : 2 = 20 (грн) – ціна котушки ниток;
3) 20 • 5 = 100 (грн) – заплатив за білі нитки;
4) 20 • 3 = 60 (грн) – заплатив за чорні нитки.
Відповідь: 100 грн заплатив за білі нитки і 60 грн заплатив за чорні нитки.
Обернена задача. Кравець заплатив 100 грн за однакові котушки білих ниток і 60 грн за такі самі котушки чорних ниток. Скільки придбав кравець котушок білих і чорних ниток окремо, якщо купив на 2 котушки більше білих ниток, ніж чорних?
1) 100 – 60 = 40 (грн) – різниця вартості ниток;
2) 40 : 2 = 20 (грн) – ціна одної котушки ниток;
3) 100 : 20 = 5 (к.) – придбав білих ниток;
4) 60 : 20 = 3 (к.) – придбав чорних ниток.
Відповідь: купили 5 котушок білих ниток і 3 котушки чорних ниток.