ГДЗ 4 клас Заїка математика завдання 353 – 373 Частина 2 Нова програма 2021 року Відповіді до підручника Ответы к учебнику

Інші завдання дивись тут...

Завдання 353 Прочитай число.

Двісті вісімдесят шість. Це число записане трьома цифрами.

Усього одиниць у числі: 286 = 2 сот. 8 дес. 6 од.

«Сусіди» числа 286 — це число 285 і число 287.

Завдання 354

а) 286 • 40 = 286 • (4 • 10) = (286 • 4) • 10 = 1144 • 10 = 11440

б) 350 • 400 = 35 • 10 • 4 • 100 = (35 • 4) • (10 • 100) = 140 • 1000 = 140000

Завдання 355

На потяг Одеса — Київ придбано 40 дитячих квитків за ціною 286 грн. Яка вартість цих квитків?

^{Короткий запис}

^{1 кв. — 286 грн}

^{40 кв. — ?}

Розв'язання

286 • 40 = 286 • (4 • 10) = (286 • 4) • 10 = 1144 • 10 = 11440 (грн)

Відповідь: вартість квитків 11440 гривень.

Завдання 356

х 25

750

х 24

960

х 320

9600

Завдання 357 Порядок дій

334 • 20 – 4719 = 1961 218 • 300 – 53800 = 11600 40000 – 39 • 500 = 20500 13150 + 250 • 20 = 18150
х 334 20 6680	_ 6680 4719 1961	х 218 300 65400	_ 65400 53800 11600	х 39 500 19500	_ 40000 19500 20500	х 250 20 5000	+13150 5000 18150

Завдання 358

1) а • b = c

^Ціна	^{Кількість}	^{Вартість}
^{300 : 10 = 30 (грн)}	¹⁰	^{300 грн}
^{30 грн}	^{300 : 30 = 10}	^{300 грн}
^{30 грн}	¹⁰	^{30 • 10 = 300 (грн)}

б) v • t = s

^{Швидкість}	^Час	^{Відстань}
^{180 : 3 = 60 (м/хв)}	^{3 хв}	^{180 м}
^{60 м/хв}	^{180 : 60 = 3 (хв)}	^{180 м}
^{60 м/хв}	^{3 хв}	^{60 • 3 = 180 (м)}

в) a • b = S

^{Довжина} ^{прямокутника}	^Ширина ^{прямокутника}	^Площа ^{прямокутника}
^{800 : 10 = 80 (м)}	^{10 м}	^{800 м2}
^{80 м}	^{800 : 80 = 10 (м)}	^{800 м2}
^{80 м}	^{10 м}	^{80 • 10 = 800 (м²)}

Завдання 359 Кількість цифр у частці

7560 : 9 = 84 (помилка, перше неповне ділене 75 на 9 у частці дасть 1 цифру, ще додати дві цифри, усього 3 цифри)

3650 : 5 = 75 (помилка, перше неповне ділене 36 на 5 у частці дасть 1 цифру, ще додати дві цифри, усього 3 цифри)

4010 : 5 = 82 (помилка, перше неповне ділене 40 на 5 у частці дасть 1 цифру, ще додати дві цифри, усього 3 цифри)

828 : 6 = 138

_7560 | 9

72 840

_36

_3650 | 5

35 730

_15

_4010 | 5

40 802

_10

_828 | 6

6 138

_22

_48

Завдання 360

Перший квиток на футбол касирка продала за номером 23064, а останній — за номером 24086. Скільки всього квитків продала касирка?

^{Короткий запис}

^{Перший номер — 23064}

^{Останній номер — 24086}

^{Всього квитків — ?}

Розв'язання

24086 – 23064 + 1 = 1023 (кв.)

Відповідь: касирка продала 1023 квитків.

Завдання 361

5957 : 7 – 13 < 7659 : 9 + 13 (838 < 864)	_5957 \| 7 56 851 _35 35 _7 7 0	_851 13 838	_7659 \| 9 72 851 _45 45 _9 9 0	+851 13 864
763 • 20 + 50 > 637 • 30 – 3900 (15310 > 15210)	х 763 20 15260	_15260 50 15310	х 637 30 19110	_19110 3900 15210
24 • 3 + 118 > 120 (190 > 120) 364 : 7 • 2 = 104 (104 = 104)	х 24 3 72	+118 72 190	_364 \| 7 35 52 _14 14 0	х 52 2 104

Завдання 362

У трьох коробках 60 банок згущеного молока. Скільки банок згущеного молока в п’яти таких коробках? У дев’яти? У тридцяти трьох?

^{Короткий запис}

^{3 к. — 60 б.}

^{5 к. — ?}

^{9 к. — ?}

^{33 к. — ?}

Розв'язання

1) 60 : 3 = 20 (б.) – банок молока в 1 коробці

2) 20 • 5 = 100 (б.) – банок молока в 5 коробках

3) 20 • 9 = 180 (б.) – банок молока в 9 коробках

4) 20 • 33 = 660 (б.) – банок молока в 33 коробках

Відповідь: у п'яти коробках є 100 банок, у дев'яти — 180 банок, у тридцять трьох — 660 банок.

Завдання 363

Скориставшись лінійкою і масштабом карти, перевір правильність позначень відстаней:

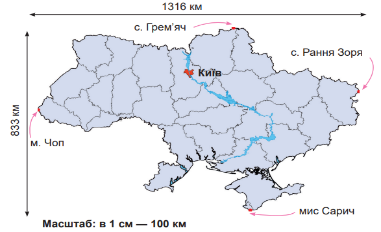
а) від крайньої північної до крайньої південної точки України;

^{Короткий запис}

^{10 мм — 100 км}

^{83 мм — ?}

Розв'язання

1) 100 : 10 = 10 (км) – в 1 мм

2) 10 • 83 = 830 (км)

б) від крайньої західної до крайньої східної точки України.

^{Короткий запис}

^{10 мм — 100 км}

^{132 мм — ?}

Розв'язання

1) 100 : 10 = 10 (км) – в 1 мм

2) 10 • 132 = 1320 (км)

Скільки (наближено) потрібно часу, щоб подолати відстань між крайніми точками з півночі до півдня, від заходу до сходу України поїздом (60–80 км/год), літаком (700 – 900 км/год), велосипедом (10–20 км/год), пішки (4–6 км/год)?

Транспорт	Швидкість	відстань між крайніми точками з півночі до півдня 830 км	відстань між крайніми точками від заходу до сходу України 1320 км
поїзд (60-80 км/год)	70 км/год	830 : 70 ≈ 12 (год)	1320 : 70 ≈ 19 (год)
літак (700-900 км/год)	800 км/год	830 : 800 ≈ 1 (год)	1320 : 800 ≈ 2 (год)
велосипед (10-20 км/год)	15 км/год	830 : 15 ≈ 55 (год)	1320 : 15 = 88 (год)
пішки (4–6 км/год)	5 км/год	830 : 5 = 166 (год)	1320 : 5 = 264 (год)

Завдання 364 Множення чисел

43 • 38 = 43 • (30 + 8) = 43 • (8 + 30) = 43 • 8 + 43 • 30 = 344 + 1290 = 1634

Завдання 365 Письмове множення

х 43

344

1290

1634

Другий неповний добуток містить нуль.

х 43

344

129

1634

Завдання 366, 567 Письмове множення

х 17

153

833

х 36

180

540

х 44

968

х 365

1095

730

8395

х 222

1110

12210

х 247

247

741

7657

25 • 19 + 6015 = 6490

24000 + 18 • 38 = 24000 + 684 = 24684

12 • 12 – 11 • 11 = 23

х 25

225

475

+ 475

6015

6490

х 18

144

684

х 12

144

х 11

121

_ 144

121

Завдання 368

До обіду господар зібрав 22 однакові ящики помідорів, а після обіду — 18 таких ящиків. Скільки кілограмів помідорів зібрав господар до обіду і після обіду, якщо всього за день він зібрав їх 480 кг?

	^{В 1 ящ.}	^{Кількість}	^Зібрав
^{До обіду}	^{Однаково}	^{22 ящ.}	^?	^{480 кг}
^{Після обіду}	^{Однаково}	^{18 ящ.}	^?	^{480 кг}

Розв'язання

1) 22 + 18 = 40 (ящ.) – всього

2) 480 : 40 = 12 (кг) – у 1 ящику

3) 12 • 22 = 264 (кг) – до обіду

4) 12 • 18 = 216 (кг) – після обіду

Відповідь: господар до обіду зібрав 264 кг помідорів, а після обіду — 216 кг.

Завдання 369

Зібрані помідори (див. № 368) господар продав по 15 грн за 1 кг. Скільки грошей отримав господар за всі помідори і скільки за помідори, зібрані до обіду і після обіду окремо?

	^Ціна	^Маса	^{Вартість}
^{До обіду}	^{15 грн}	^{264 кг}	^?	^?
^{Після обіду}	^{15 грн}	^{216 кг}	^?	^?

Розв'язання

1) х 264

1320

264

3960 (грн) – до обіду

2) х 216

1080

216

3240 (грн) – після обіду

3) + 3960

3240

7200 (грн)

Відповідь: господар отримав 7200 грн.

Завдання 370

На кожній круговій діаграмі позначено числові дані, що є в текстах чи розв’язках задач № 368 і № 369

Дані вписані правильно. Вони позначають співвідношення кількості, маси, вартості.

Діаграми на рисунках однакові, бо на них зображені пропорційні відомості про ті самі об'єкти.

Завдання 371 Письмове множення

х 76

608

228

2888

х 324

25920

1325 • 47 – 3280 = 58995

х 1325

8645

5300

62275

_ 62275

3280

58995

Завдання 372

Столяр розрізає бруси завдовжки 2 м, завширшки і заввишки по 2 дм на кубики з ребром 1 дм. За годину він розрізає 5 брусів. Скільки кубиків зробить столяр за одну зміну (7 год)? Виконай схематичний рисунок бруса.

^{Короткий запис}

^{Брус — 20 дм х 2 дм х 2 дм}

^{Кубик — 1 дм х 1 дм х 1 дм}

^{За 1 год — 5 бр. по ? к.}

^{За 7 год — ? к.}

Розв'язання

2 м = 2 дм

1) 20 • 2 • 2 = 80 (дм³) – має 1 брус

2) 1 • 1 • 1 = 1 (дм³) – має 1 кубик

3) 80 : 1 = 80 (к.) – кубиків нарізає з 1 бруса

4) 80 • 5 = 400 (к.) – кубиків нарізає за 1 год

5) 400 • 7 = 2800 (к.) – кубиків зробить за 7 год