© ГДЗ 8next.com, 2013, 2018, 2022
Запитання
1. Сформулюйте сполучну властивість множення. Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого і третього чисел.
2. Як записують у буквеному вигляді сполучну властивість множення? (ab)c = а(Ьс)
3. Сформулюйте розподільну властивість множення відносно додавання. Щоб число помножити на суму двох чисел, можна це число помножити на кожний доданок і отримані добутки додати.
4. Як записують у буквеному вигляді розподільну властивість множення відносно додавання? a(b + с) = ab + ас, звідси випливає, що ab + ас = а (Ь + с)
Як записують у буквеному вигляді розподільну властивість множення відносно віднімання? а(Ь ─ с) = ab ─ ас, якщо b > с або b = с
Розв’язуємо усно
Завдання 1 Добуток чисел 3 і 8 помножте на 100.
(3 • 8) • 100 = 2400
Завдання 2 Число 3 помножте на добуток чисел 8 і 100.
3 • (8 • 100) = (3 • 8) • 100 = 2400
Завдання 3 Знайдіть добуток суми чисел 8 і 7 та числа 6 .
(8 + 7) • 6 = 8 • 6 + 7 • 6 = 48 + 42 = 90
Завдання 4 Знайдіть суму добутків чисел 8 і 6 та чисел 7 і 6 .
8 • 6 + 7 • 6 = 48 + 42 = 90
Завдання 5 Чи можна подати число 6 у вигляді добутку 100 множників?
|
6 • (1 • 1 ... 1 • 1) = 6 99 множників |
3 • 2 • (1 • 1 ... 1 • 1) = 6 98 множників |
Завдання 6 В інкубаторі було 1000 яєць. Із кожних 100 яєць вилупилося 95 курчат. Скільки всього вилупилося курчат?
Короткий запис
100 яєць ─ 95 курчат
1000 яєць ─ ?
Розв'язання
1) 1000 : 100 = 10 (р.) ─ у стільки разів більше яєць.
2) 95 • 10 = 950 (к.) ─ курчат вилупилося.
Відповідь: вилупилось 950 курчат.
Завдання 7 (Задача-жарт) Двоє батьків і двоє синів з’їли 3 яблука, причому кожен із них з’їв ціле яблуко. Чи може таке бути? Може. Дідусь і батько є двома батьками, водночас батько є сином дідуся, а внук є сином батька, разом троє людей.
Вправи
Вправа 452° Обчисліть зручним способом:
1) 2 • 328 • 5 = (2 • 5) • 328 = 328 • 10 = 3280
2) 125 • 43 • 8 = (125 • 8) • 43 = 1000 • 43 = 43000
3) 25 • 243 • 4 = 243 • (25 • 4) = 243 • 100 = 24300
4) 4 • 36 • 5 = 36 • (4 • 5) = 36 • 20 = 720
5) 50 • 236 • 2 = 236 • (2 • 50) = 236 • 100 = 23600
6) 250 • 3 • 4 = 3 • (250 • 4) = 3 • 1000 = 3000
Вправа 453° Обчисліть зручним способом:
1) 4 • 17 • 25 = 17 • (4 • 25) = 17 • 100 = 1700
2) 5 • 673 • 2 = 673 • (5 • 2) = 673 • 10 = 6730
3) 8 • 475 • 125 = 475 • (8 • 125) = 475 • 1000 = 475000
4) 73 • 5 • 4 = 73 • 20 = 1460
5) 2 • 916 • 50 = 916 • (2 • 50) = 916 • 100 = 91600
6 ) 5 • 9 • 200 = 9 • (200 • 5) = 9 • 1000 = 9000
Вправа 454° Спростіть вираз:
1) 13 • 2а = (13 • 2) • а = 26а
2) 9х • 8 = (9 • 8) • х = 72х
3) 23 • 4b = (23 • 4) • b = 92b
4) 28 • у • 5 = (14 • 2 • 5) • у = 14 • (2 • 5) • у = (14 • 10) • у = 140у
5) 6а • 8b = (6 • 8) • (а • b) = 48аb
6) 11х • 14у = (11 • 14) • (х • у) = 154ху
7) 27 m • 3 n = (27 • 3) • (m • n) = 81mn
8) 4а • 8 • Ь • 3 • с = (4 • 8 • 3) • (а • b • с) = 96аbс
9) 12х • 3у • 5z = (12 • 5 • 3) • (х • у • z)=(6 • 2 • 5 • 3) • (х • у • z)=(2 • 5) • (6 • 3) • (х • у • z)=
= (10 • 18) (х • у • z) = 180хуz
Вправа 455° Спростіть вираз:
1) 12 • Зх = (12 • 3) • х = 36х
2) 10х • 6 = (6 • 10) • х = 60х
3) 5а • 7b = (5 • а) • (7 • b) = (5 • 7) • (а • b) = 35аb
4) 8m • 12n = (8 • m) • (12 • n) = (8 • 12) • (m • n) = 96mn
5) 2а • Зb • 4с = (2 • а) • (3 • b) • (4 • с) = (2 • 3 • 4) • (а • b • с) = 24аbс
6) 5х • 2у • 10z = (5 • х) • (2 • у) • (10 • z) = (5 • 2 • 10) • (х • у • z) = 100хуz
Вправа 456° Обчисліть значення виразу найзручнішим способом:
1) 318 • 78 + 318 • 22 = 318 • (78 + 22) = 318 • 100 = 31800
2) 856 • 92 - 853 • 92 = 92 • (856 ─ 853) = 92 • 3 = (90 + 2) • 3 = 270 + 6 = 276
3) 943 • 268 + 943 • 232 = 943 • (268 + 232) = 943 • 500 = (900 + 40 + 3) • 500 =
= 450000 + 20000 + 1500 = 471500
4) 65 • 246 - 65 • 229 - 65 • 17 = 65 • (246 - 229 - 17) = 65 • 0 = 0
Вправа 457° Обчисліть значення виразу найзручнішим способом:
1) 47 • 632 + 632 • 53 = 632 • (47 + 53) = 632 • 100 = 63200
2) 598 • 49 ─ 597 • 49 = 49 • (598 ─ 597) = 49 • 1 = 49
3) 754 • 324 ─ 754 • 314 = 754 • (324 ─ 314) = 754 • 10 = 7540
4) 37 • 46 ─ 18 • 37 + 37 • 72 = 37 • (46 ─ 18 + 72) = 37 • 100 = 3700
Вправа 458° Розкрийте дужки:
1) 2 (а + 5) = 2 • а + 2 • 5 = 2а + 10
2) 8 (7 ─ х) = 8 • 7 ─ 8 • х = 56 - 8х
3) 12 (х + у) = 12 • х + 12 • у = 12х + 12у
4) (с ─ 9) • 11 = 11 • с ─ 11 • 9 = 11 с - 99
5) (8 + у) • 16 = 16 • 8 + 16 • у = 128 + 16у
6) 15 ( 4а ─ 3) = 15 • 4а - 15 • 3 = 60а - 45
7) 7 (6а + 8b) = 7 • 6а + 7 • 8b = 42а + 56b
8) 10 (2m ─ 3n + 4k = 10 • 2m - 10 • 3n + 10 • 4k = 20m - 30n + 40k
9) (24x + 17у ─ 36z) • 4 = 4 • 24х + 4 • 17у ─ 4 • 36z = 96х + 68у - 144z
Вправа 459° Розкрийте дужки:
1) 4 (а + 2) = 4 • а + 4 • 2 = 4а + 8
2) 3 (m ─ 5) = 3 • m ─ 3 • 5 = 3m - 15
3) (р ─ q) • 9 = 9 • р ─ 9 • q = 9p - 9q
4) 12 (а + b) = 12 • а + 12 • b = 12а + 12b
5) 5 (2m ─ 1) = 5 • 2m ─ 5 • 1 = 10m - 5
6) (Зс + 5d) • 14 = 14 • 3с + 14 • 5d = 42с + 70d
Вправа 460° Спростіть вираз:
1) 6а + 8а = (6 + 8) • а = 14а
2) 28с ─ 15с = (28 ─ 15) • с = 13с
3) m + 29m = (1 + 29) • m = 30m
4) 98р ─ р = (98 ─ 1) • р = 97р
5) 4х + 13х + 15х = (4 + 13 + 15) • х = 32х
6) 67z ─ 18z + 37 = (67 ─ 18) • z + 37= 49z + 37
Вправа 461° Спростіть вираз:
1) 13b + 19b = (13 + 19) • b = 32b
2) 44d ─ 37d = (44 ─ 37) • d= 7d
3) 34n + n = (34 + 1) • n = 35n
4) 127q ─ q = (127 ─ 1) • q = 126q
5) 36у ─ 19у + 23у = (36 ─ 19 + 23) • у = 40у
6) 49а + 21а + З0 = (49 + 21) • а + 30 = 70а + 30
Вправа 462 Спростіть вираз і знайдіть його значення.
1) 25х • 4у, якщо х = 12, у = 11
Якщо х = 12, у = 11, тоді 25х • 4у = 100 • х • у = 100 • (12 • 11) = 100 • 132 =
= 13200
2) 8k • 125с, якщо k = 58, с = 8
Якщо k = 58, с = 8, тоді 8k • 125с = 1000 • (k • c) = 1000 • (58 • 8) = 464 • 1000 =
= 464000
Вправа 463 Спростіть вираз і знайдіть його значення:
1) 5а • 20b, якщо а = 4, b = 68;
Якщо а = 4, b = 68, тоді 5а • 20b = 100 • а • b = 100 • (68 • 4) = 100 • 272 =
= 27200
2) 4 m • 50n, якщо m = 22, n = 34.
Якщо m = 22, n = 34, тоді 4m • 50n = 200 • m • n = 200 • (22 • 34) = 200 • 748 =
= 149600
Вправа 464 Спростіть вираз і обчисліть його значення:
1) 1Зр + 37р, якщо р = 14;
Якщо р = 14, тоді 13р + 37р = 50р = 50 • 14 = 700
2) 38х + 17х - 54х + х , якщо х = 678;
Якщо х = 678, тоді 38х + 17х ─ 54х + х = 2х = 2 • 678 = (600 + 70 + 8) • 2 =
= 1200 + 140 + 16 = 1356
3) 86с - 35с - с + 296, якщо с = 47.
с = 47, тоді 86с ─ 35с ─ с + 296 = 50с + 296 = 50 • 47 + 296 = 2350 + 296 = 2646
Вправа 465 Спростіть вираз і обчисліть його значення:
2) 54а - 39а, якщо а = 26;
Якщо а = 26, тоді 54а ─ 39а = 15а = 15 • 26 = 390
3) 18m - 5m + 7m , якщо m = 394;
Якщо m = 394, тоді 18m ─ 5m + 7m = 20m = 20 • 394 = (300 + 90 + 4) • 20 =
= 6000 + 1800 + 80 = 7880
4) 19z - 12z + 33z - 14, якщо z = 82.
Якщо z = 82, тоді 19z ─ 12z + 33z ─ 14 = 40z ─ 192 = 40 • 82 ─ 14 =
= 3280 ─ 14 = 33266
Вправа 466 Обчисліть зручним способом:
1) 16 • 25 = (4 • 4) • 25 = 4 • (4 • 25) = 4 • 100 = 400
2) 25 • 8 • 5 = 25 • (4 • 2) • 5 = (25 • 4) • (2 • 5) = 100 • 10 = 1000
3) 15 • 12 = (3 • 5) • (2 • 6) = (3 • 6) • (5 • 2) = 18 • 10 = 180
4) 375 • 24 = 375 • (4 • 6) = (375 • 4) • 6 = 1500 • 6 = 9000
Вправа 467 Обчисліть зручним способом:
1) 25 • 4 • 6 = 100 • 6 = 600
2) 125 • 25 • 32 = 125 • 25 • (4 • 8) = (125 • 8) • (25 • 4) = 1000 • 100 = 100000
3) 75 • 36 = 75 • 4 • 9 = 300 • 9 = 2700
4) 96 • 50 = (90 + 6) • 50 = 90 • 50 + 6 • 50 = 4500 + 300 = 4800
Вправа 468 Обчисліть значення виразу зручним способом:
1) 43 • 64 + 43 • 23 - 87 • 33 = 43 • (64 + 23) - 87 • 33 = 43 • 87 - 87 • 33 =
= 87 • (43 ─ 33) = 87 • 10 = 870
2) 84 • 53 ─ 84 • 28 + 16 • 61 ─ 16 • 36 = 84 • (53 ─ 28) + 16 • (61 ─ 36) =
= 84 • 25 + 16 • 25 = 25 • (84 + 16) = 25 • 100 = 2500
Вправа 469 Обчисліть значення виразу зручним способом:
1) 93 • 24 ─ 27 • 24 + 66 • 76 = 24 • (93 ─ 27) + 66 • 76 = 24 • 66 + 66 • 76 =
= 66 • (24 + 76) = 66 • 100 = 6600
2) 82 • 46 + 82 • 54 + 135 • 18 ─ 18 • 35 = 82 • (46 + 54) + 18 • (135 ─ 35) =
= 82 • 100 + 18 • 100 = 100 • (82 + 18) = 100 • 100 = 10000
Вправа 470 Дії з іменованими величинами
|
1) 2 км 56 м • 68 = 2056 м • 68 = 139808 м = 139 км 808 м
2) 7 грн 9 коп. • 54 = 709 коп. • 54 = 38286 коп. = 382 грн 86 коп.
3) 4 км 90 м • 43 = 4090 м • 43 = 1758790 м = 175 км 870 м
4) 3 т 5 ц 65 кг • 8 = 3565 кг • 8 = 28520 кг = 28 т 5 ц 20 кг
5) 3 год 48 хв • 25 = 228 хв • 25 = 5700 хв = 95 год
6) 5 год 12 хв 36 с • 15 = 75 год 180 хв 540 с = 78 год 9 хв
|
||||
|
х 2056 68 16448 12336 139808 |
х 709 54 2836 3545 38286 |
х 4090 43 1227 1636 175870 |
х 3565 8 28520 |
х 228 25 1140 456 5700 |
Вправа 471 Одиниці вимірювання
|
1) 8 ц 26 кг • 27 = 826 кг • 27 = 22302 кг = 223 ц 2 кг
2) 14 грн 80 коп. • 40 = 1480 коп. • 40 = 59200 коп. = 592 грн
3) 6 т 45 кг • 82 = 6045 кг • 82 = 495690 кг = 495 т 690 кг
4) 5 м 8 см • 42 = 508 см • 42 = 21336 см = 213 м 36 см
5) 7 хв 5 с • 24 = 425 с • 24 = 10200 с = 170 хв
або
7 хв 5 с • 24 = 7 хв • 24 + 5 с • 24 = 168 хв + 120 с = 168 хв + 2 хв = 170 хв
6) 4 доби 6 год • 12 = 102 год • 12 = 1224 год = 51 доба
або
4 доби 6 год • 12 = 4 доби • 12 + 6 год • 12 = 48 діб 72 год = 48 діб + 3 доби =
= 51 доба
|
|||||
|
х 826 27 5782 1652 22302 |
х 1480 40 59200 |
х 6045 82 12090 48360 495690 |
х 508 42 1016 2032 21336 |
х 425 24 1700 850 10200 |
х 102 12 204 102 1224 |
Вправа 472 Скількома нулями закінчується добуток усіх натуральних чисел:
1 ) від 1 до 10 включно; Два нулі (5 • 2 • 10 = 10 • 10 = 100)
2) від 15 до 24 включно; Два нулі (15 • 18 • 20 = 5400)
3) від 10 до З0 включно; Шість нулів
(10 • 20 • 30 • 15 • 12 • 25 • 14 = 378000000 дає 6 нулів)
4) від 1 до 100 включно? Двадцять два нулі
(10 • 20 • 30 • 40) • (5 • 10 • 2) • (60 • 70 • 80 • 90) • 100 • (5 • 8) • (15 • 12) •
• (25 • 22) • (35 • 32) • (45 • 42) • (55 • 52) • (65 • 62) • (75 • 72) • (85 • 82) •
• (95 • 92) дають 4 + 2 + 4 + 2 + 10 = 22 нулі.
Примітка. Беремо до уваги множники, які дають у добутку нулі (множники, які закінчуються 0, та добуток множників, які закінчуються 5, та парного числа).
Вправи для повторення
Вправа 473 Кут ABC — прямий, промінь ВР — бісектриса кута АВК, промінь ВМ — бісектриса кута СВК (рис. 152). Яка градусна міра кута МВР?
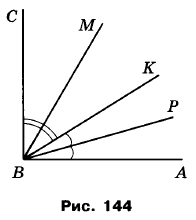
Розв'язання
За властивістю кутів <МВР = <МВК + <КВР
З однієї сторони <АВС = 90°, а з іншої сторони
<АВС = <СВМ + <МВК + <КВР + <РВА
<АВС = 2<МВК + 2<КВР
<АВС = 2 (<МВК + <КВР)
<МВР = <МВК + <КВР = <АВС : 2 = 90° : 2 = 45°
Відповідь: <МВР = 45°
Вправа 474 По подвір'ї бігали кошенята та курчата. Вони разом мали 14 голів і 38 ніг. Скільки кошенят і скільки курчат бігало по двору?
Розв'язання
1-й спосіб
Припустимо, що у всіх тварин по 2 ноги, тоді
1) 38 : 2 = 19 (г.) ─ голів у всіх тварин.
2) 19 ─ 14 = 5 (г.) ─ голів припадає на кошенят.
2) 14 ─ 5 = 9 (г.) ─ голів припадає на курчат.
2-й спосіб
У курчат по 2 ноги, у кошенят по 4 ніг.
1) 14 • 2 = 28 (ніг) ─ мали би тварини з двома ногами.
2) 38 ─ 28 = 10 (ніг) ─ решта ніг кошенят.
3) 10 : 2 = 5 (к.) ─ кошенят.
4) 14 ─ 5 = 9 (к.) ─ курчат.
3-й спосіб
Нехай х ─ кошенята, тоді 4х - ніг всіх кошенят, (14 ─ х) ─ курчат, 2 • (14 ─ х) ─ ніг у всіх курчат, тоді складемо рівняння
4х + 2 • (14 ─ х) = 38
4х + 28 ─ 2х = 38
2х + 28 = 38
2х = 38 ─ 28
2х = 10
х = 10 : 2
х = 5 ─ кошенят.
14 ─ х = 14 ─ 5 = 9 ─ курчат.
Відповідь: по подвір'ї бігало 5 кошенят і 9 курчат.
Вправа 475 (Знайдіть помилку) Василь Ледащенко замість того, щоб самостійно розв’язати задачу 465 (3), скористався ГДЗ і списав таке: 19z – 12z + 33z – 14 = 26z = 26 • 82 = 2132. Знайдіть помилку в цьому «розв’язанні».
Правильне розв'язання.
19z ─ 12z + 33z ─ 14 = 40z ─ 192 = 40 • 82 ─ 14 = 3280 ─ 14 = 33266
Учимося застосовувати математику
Вправа 476 На фермі є 78 корів, кожна з яких дає за день 12 л молока. Молоко з ферми вивозять у бідонах ємністю 40 л. Одного дня на фермі був 21 порожній бідон. Чи вистачить бідонів, щоб вивезти з ферми молоко, яке надоїли за цей день?
Короткий запис
Усього — ?, 76 к. по 12 л кожна
Розлили — ? б. по 40 л
Розв'язання
1) 12 • 76 = 936 (л) ─ усього молока дали корови.
2) 936 : 40 = 23 (ост. 16) ─ потрібно 24 бідони.
21 < 24
Відповідь: не вистачить.
Вправа 477 Сім’я із двох дорослих і дитини може поїхати на відпочинок поїздом або на автомобілі. Квиток на поїзд для одного дорослого коштує 870 грн, а для дитини — у два рази менше. Автомобіль витрачає 12 л бензину на 100 км, а ціна одного літра бензину становить 26 грн. Відстань до місця відпочинку по автошляху дорівнює 600 км. Яким видом транспорту цій сім’ї дешевше доїхати до місця відпочинку?
Розв’язання
1) 870 : 2 = 435 (грн.) ─ ціна квитка на поїзд для дитини.
2) 870 + 435 = 1305 (грн.) ─ вартість поїздки поїздом.
3) 600 : 100 = 6 (разів) ─ у стільки разів більше бензину витратять.
4) 12 • 6 = 72 (л) ─ літрів бензину витратять на дорогу.
5) 26 • 72 = 1872 (грн.) ─ вартість поїздки автомобілем.
Відповідь: поїздом дешевше.
Задача від Мудрої Сови
Вправа 478 У 5 класі навчаються троє друзів: Михайлик, Дмитрик і Сашко. Один із них займається футболом, другий — плаванням, а третій — боксом. У футболіста немає ні брата, ні сестри, він наймолодший із друзів. Михайлик старший за боксера й товаришує із сестрою Дмитрика. Яким видом спорту займається кожний із друзів?
Розв'язання
Дмитрик має сестру.
У футболіста нема сестри, він не Дмитрик, він найменший, тому він не Михайлик.
Футболіст Сашко.
Михайлик старший від боксера, тому боксер Дмитрик.
Михайлик займається плаванням.
----------------------------- у підручниках 2013 і 2018 року ------------------------------
Запитання
5 Що випливає з переставної та сполучної властивостей множення? При множенні кількох чисел множники можна міняти місцями та брати в дужки, тим самим визначаючи порядок обчислень.
Вправа 1 Заповніть ланцюжок обчислень.
Вправа 450. У першому ящику на 14 кг апельсинів менше, ніж у другому, і на 18 кг більше, ніж у третьому. Скільки кілограмів апельсинів міститься в усіх трьох ящиках разом, якщо в другому ящику їх 44 кг?
Розв'язання
1) 44 ─ 14 = 30 (кг) ─ у першому ящику.
2) 30 ─ 18 = 12 (кг) ─ у третьому ящику.
3) 30 + 44 + 12 = 86 (кг)
Відповідь: у трьох ящиках разом 86 кг апельсинів.
Вправа 439* Обчисліть найзручнішим способом значення виразу:
1) Якщо b = 602, тоді 398 • 36 + 36b = 36 • (398 + b) = 36 • (398 + 602) =
= 36 • 1000 = 36000
2) Якщо b = 83, тоді 986b ─ 86 • 83 = 986 • 83 ─ 86 • 83 = 83 • (986 ─ 86) =
= 83 • 900 = 74700
Вправа 440* Обчисліть найзручнішим способом значення виразу:
1) 631 • 18 + х • 369, якщо х = 18;
Якщо х = 18, тоді 631 • 18 + х • 369 = 631 • 18 + 18 • 369 = 18 • (631 + 369) =
= 18 • 1000 = 18000
2) 58а - 58 • 824, якщо а = 1024.
Якщо а = 1024, тоді 58а ─ 58 • 824 = 58 • (а ─ 824) = 58 • (1024 ─ 824) = 58 • 200 =
= (50 + 8) • 200 = 50 • 200 + 8 • 200 = 10000 + 1600 = 11600
Вправа 441* Спростіть вираз і обчисліть його значення:
2) 72b - 43b, якщо b = 54;
Якщо b = 54, тоді 72b - 43b = 29b = 29 • 54 = 1566
Вправа 442* Спростіть вираз і обчисліть його значення:
1) 34х + 66х, якщо х = 8;
1) Якщо х = 8, тоді 34х + 66х = 100х = 100 • 8 = 800
4) 19z - 12z + 33z - 192, якщо z = 82.
Якщо z = 82, тоді 19z ─ 12z + 33z ─ 192 = 40z ─ 192 = 40 • 82 ─ 192 =
= 3280 ─ 192 = 3088