Інші завдання дивись тут ...

© ГДЗ 8next.com, 2013, 2018, 2022

Питання

1. Які властивості площі фігури ви знаєте? Рівні фігури мають рівні площі. Площа фігури дорівнює сумі площ фігур, з яких вона складається.

2. Який квадрат називають одиничним? Квадрат, сторона якого дорівнює одиничному відрізку, називають одиничним. 

3. Які одиниці виміру площі ви знаєте? Метр (м), сантиметр (см), дециметр (дм), міліметр (мм). 

4. Що означає виміряти площу фігури? Виміряти площу фігури — це означає підрахувати, скільки одиничних квадратів у ній уміщується.

5. Чому дорівнює площа прямокутника? Площа прямокутника дорівнює добутку довжин його сусідніх сторін: S = ab, де S — площа прямокутника, а і b — довжини його сусідніх сторін, виражені в одних і тих самих одиницях.

6. За якою формулою обчислюють площу квадрата? Оскільки у квадрата всі сторони рівні, то його площу обчислюють за формулою S = а², де S — площа квадрата, а — довжина його сторони.

 

Розв’язуємо усно

Завдання 1 Одиниці вимірювання

Розв’язання

1) 40 : 5 = 8 (км/год) – швидкість човна.

2) 24 : 8 = 3 (год) – треба часу.

Відповідь: 24 км човен пройде за 3 год.

 

Завдання 4 Скільки літрів води може перекачати насос за 8 хв, якщо 5 таких насосів за 6 хв перекачують 450 л води?

^{Короткий запис}

^{5 н., 6 хв — 450 л}

^{1 н., 8 хв — ?}

Розв’язання

1) 450 : 5 = 90 (л) – води качає 1 насос за 6 хв.

2) 90 : 6 = 15 (л) – води качає 1 насос за 1 хв.

3) 15 • 8 = 120 (л) – води перекачає насос за 8 хв.

Відповідь: за 8 хв насос перекачає 120 л води.

 

Завдання 5 Яку одну й ту саму цифру треба поставити замість зірочок, щоб запис 1* + 3* + 5* = 111 став правильною рівністю? 17 + 37 + 57 = 111

 

Вправи

Вправа 595° 

1) Скільки квадратних сантиметрів містить 1 дм²? 1 м²?

1 дм² = 10 см • 10 см = 100 см²

1 м² = 100 см • 100 см = 10000 см²

2) Скільки квадратних метрів містить 1 км²? 

1 км² = 1000 м • 1000 м = 1000000 м²

 

Вправа 596° Скільки нулів треба записати замість крапок, щоб утворилася правильна рівність:

1) 1 м² = 100 дм² ; Два нулі

2) 1 м² = 10000 см² ; Чотири нулі

3) 1 км² = 100 га? Два нулі

 

Вправа 597° Які одиниці площі доцільно використовувати для вимірювання площі:

Рівні площі мають фігури: 2 і 3.

Ці фігури не є рівними, оскільки вони не суміщаються при накладанні.

 

Вправа 599° Вважаючи, що довжина сторони клітинки дорівнює 1 см, знайдіть площі фігур, зображених на рисунку 158.

^{Короткий запис}

^{а — 14 см}

^{b — 8 см}

^S — ?

Розв’язання

S = a • b = 14 см • 8 см = 112 (см²) – площа прямокутника.

Відповідь: площа прямокутника 112 см².

 

Вправа 601° Обчисліть площу квадрата зі стороною 7 дм.

^{Короткий запис}

^{а — 7 дм}

^S — ?

Розв’язання

S = a • а = 7 дм • 7 дм = 49 (дм²) – площа квадрата.

Відповідь: площа квадрата 49 дм².

 

Вправа 602° Сторона прямокутника дорівнює 16 см, а сусідня сторона на 6 см більша за неї. Обчисліть площу прямокутника.

^{Короткий запис}

^{а — 16 см}

^{b — ?, на 6 см більша}

^S — ?

Розв’язання

1) 16 + 6 = 22 (см) – сусідня сторона.

2) 16 см • 22 см = 352 (см²)  – площа прямокутника.

Відповідь: площа прямокутника 352 см². 

 

Вправа 603° Сторона прямокутника дорівнює 48 см, а сусідня сторона у 8 разів менша від неї. Обчисліть площу

прямокутника.

^{Короткий запис}

^{а — 16 см}

^{b — ?, у 8 разів менша}

^S — ?

Розв’язання

1) 48 : 8 = 6 (см) – сусідня сторона.

2) 48 см • 6 см = 288 (см²) – площа прямокутника.

Відповідь: площа прямокутника 288 см².

 

Вправа 604 Периметр прямокутника дорівнює 162 дм, а одна зі сторін — 47 дм. Знайдіть площу прямокутника.

^{Короткий запис}

^{Периметр — 162 дм}

^{Сторона — 47 см}

^{Площа — ?}

Розв’язання

1) 162 : 2 = 81 (дм) – півпериметр прямокутника

2) 81 – 47 = 34 (дм) – друга сторона прямокутника.

3) S = 47 дм • 34 дм = 1598 (дм²) – площа прямокутника.

Відповідь: площа прямокутника 1598 дм².

 

Вправа 605 Периметр прямокутника дорівнює 96 м, і він у 8 разів більший за одну зі сторін прямокутника. Знайдіть площу прямокутника.

^{Короткий запис}

^{Периметр — 96 м, він у 8 разів менший за сторону}

^{Сторона — ?}

^{Площа — ?}

Розв’язання

1) 96 : 2 = 48 (см) – півпериметр прямокутника.

2) 96 : 8 = 12 (см) – одна сторона.

3) 48 – 12 = 36 (см) – друга сторона.

4) S = 36 см • 12 см = 432 (см²) – площа прямокутника.

Відповідь: площа прямокутника 432 см².

 

Вправа 606 Знайдіть площу квадрата, периметр якого дорівнює 96 см.

^{Короткий запис}

^{Периметр — 96 см}

^{Площа — ?}

Розв’язання

1) 96 : 4 = 24 (см) – сторона квадрата.

2) S = 24 см • 24 см = 576 (см²) – площа квадрата.

Відповідь: площа квадрата дорівнює 576 см².

 

Вправа 607 Периметр прямокутника дорівнює 4 м 8 дм, одна з його сторін у 5 разів більша за сусідню сторону. Знайдіть площу прямокутника.

^{Короткий запис}

^{Периметр — 6 дм 8 см}

^{Сторона — ?, у 5 разів менша, ніж сусідня сторона}

^{Площа — ?}

Розв’язання

Нехай х (дм) – одна сторона, 5х (дм) – друга сторона. Складемо рівняння

(х + 5х) • 2 = 48

6х • 2 = 48

6х = 48 : 2

6х = 24

х = 24 : 6 

х = 4 (дм) – одна сторона.

5х = 5 • 4 = 20 (дм) – друга сторона.

S = 20 дм • 4 дм = 80 (дм²) – площа прямокутника. 

 

Вправа 608 Периметр прямокутника дорівнює 6 дм 8 см, одна з його сторін на 1 дм 6 см менша від сусідньої сторони. Знайдіть площу прямокутника.

^{Короткий запис}

^{Периметр — 6 дм 8 см}

^{Сторона — ?, на 1 дм 6 см менша}

^{Площа — ?}

Розв’язання

6 дм 8 см = 68 см,  1 дм 6 см = 16 см

Нехай х (см) – одна сторона, x+16 (cм) – друга сторона. Складемо рівняння

x + (х + 16) • 2 = 68

(2x + 16) • 2 = 68

2х + 16 = 68 : 2

2х + 16 = 34

2х = 34 - 16 

x = 18 : 2

х = 9 (см) – одна сторона.

х + 16 = 9 + 16 = 25 (см) – друга сторона.

S = 25 дм • 9 дм = 225 (см²) – площа прямокутника. 

 

Вправа 609 Виразіть:

1) в арах: 12 га; 6 га 28 а; 2 км² 14 га 5 а; 32 400 м²;

12 га = 1200 а

6 га 28 а = 628 а

2 км² 14 га 5 а = 20000 а + 1400 а + 5а = 21405 а

32 400 м² = 324 а

2) у квадратних метрах: 17 а; 8 га; 5 га 72 а;

17 а = 1700 м²

8 га =  80000 м²

5 га 72 а = 50000 м² + 7200 м² = 57200 м²

3) у гектарах і арах: 530 а; 1204 а; 16 300 м².

530 а = 5 га 30 а

1204 а = 12 га 4 а

16 300 м² = 1 га 63 а

  

Вправа 610 Виразіть:

1) у квадратних сантиметрах: 4 м²; 16 м² 19 дм²; 16 дм²;

4 м² = 40000 см²

16 м² 19 дм² = 160000 см² + 1900 см² = 161900 см²

16 дм² = 1600 см² 

2) у гектарах: 340 000 м²; 14 км²; 5 км² 18 га.

340000 м² = 34 га

14 км² =  1400 га

5 км² 18 га = 500 га + 18 га = 518 га

 

Вправа 611 Поле прямокутної форми має площу 56 а, його довжина — 80 м. Обчисліть периметр поля.

^{Короткий запис}

^{Площа — 56 а}

^{Довжина — 80 м}

^{Периметр — ?}

Розв’язання

56 а = 56 • 100  м² = 5600 м²

1) 5600 : 80 = 70 (м) – ширина поля.

2) Р = (80 м + 70 м) • 2 = 150 м • 2 = 300 (м) – периметр поля.

Відповідь: периметр поля 300 м.  

 

Вправа 612 Поле прямокутної форми має площу 48 а, його ширина — 150 м. Обчисліть периметр поля.

^{Короткий запис}

^{Площа — 48 а}

^{Ширина — 150 м}

^{Периметр — ?}

Розв’язання

48 а = 48 • 100 м² = 4800 м²

1) 4800 : 150 = 480 : 15 = 32 (м) – довжина поля.

2) Р = (150 м + 32 м) • 2 = 364 (м) – периметр поля.

Відповідь: периметр поля 364 м.

 

Вправа 613 Обчисліть периметр і площу фігури, зображеної на рисунку 159 (розміри дано в сантиметрах). Чи є на рисунку 159 зайві дані для обчислення периметра многокутника?

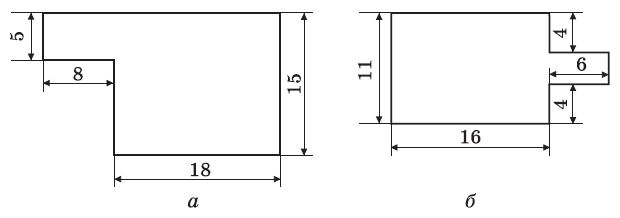
Розв’язання

Варіант а)

1) Р = 18 см + 15 см + (18 см + 8 см) + 5 см + 8 см + (15 см – 5 см) = 82 (см) – периметр фігури.

2) S = 18 см • 15 см + 8 см • 5 см = 270 см² + 40 см² = 310 (см²) – площа фігури.

Відповідь: периметр дорівнює 82 см, площа дорівнює 310 см².

Варіант б)

1) Р = 16 см + 4 см + 6 см + (11 см – 4 см – 4 см) + 6 см + 4 см + 16 см + 11 см = 66 (см) – периметр ділянки.

2) S = 11 см • 16 см + 6 см • (11 см – 4 см – 4 см) = 176 см² + 18 см² = 194 (см²) – площа ділянки.

Відповідь: периметр дорівнює 66 см, площа дорівнює 194 см².

 

Вправа 614 Обчисліть периметр і площу многокутника, зображеної на рисунку 160 (розміри дано в сантиметрах). 

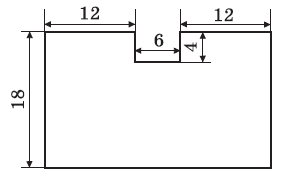
Розв’язання

1) Р=(12 см + 6 см + 12 см) + 18 см + (12 см + 4 см + 6 см + 4 см + 12 см) + 18 см=

= 104 (см) – периметр фігури.

2) S =  18 см • 30 см – 6 см • 4 см = 540 см² – 24 см² = 516 (см²) – площа ділянки.

Відповідь: периметр дорівнює 104 см, площа дорівнює 516 см².

 

Вправа 615 (Домашня практична робота) На папері в клітинку зобразіть будь-яку фігуру, що складається з 12 клітинок. Вважаючи, що довжина сторони клітинки дорівнює 5 мм, знайдіть площу цієї фігури у квадратних сантиметрах. Порівняйте свою відповідь із результатами однокласників і однокласниць.

Розв’язання

1) 5 • 5 = 25 (мм²) – площа одної клітинки.

2) 25 • 12 = 300 (мм²) = 3 (см²) – площа фігури.

Відповідь: площа фігури 3 см².

 

Вправа 616 Квадрат із стороною 12 см і прямокутник, довжина якого дорівнює 18 см, мають однакові площі. Знайдіть периметр прямокутника.

Розв’язання

1) S = 12 см • 12 см = 144 (см²) – площа квадрата або прямокутника.

2) 144 : 18 = 8 (см) – ширина прямокутника.

3) Р = (18 см + 8 см) • 2 = 52 (см) – периметр прямокутника.

Відповідь: периметр прямокутника 52 см.

 

Вправа 617 Квадрат і прямокутник мають рівні площі, сусідні сторони прямокутника дорівнюють 3 см і 12 см. Знайдіть периметр квадрата.

Розв’язання

1) S = 3 см • 12 см = 36 см² – площа прямокутника або квадрата.

6 см – сторона квадрата.

2) Р = 6 см • 4 = 24 см – периметр квадрата.

Відповідь: периметр квадрата 24 см.

 

Вправа 618 Ширина прямокутника дорівнює 26 см. На скільки квадратних сантиметрів збільшиться площа цього прямокутника, якщо його довжину збільшити на 4 см?

Розв’язання

Нехай х (см) – довжина прямокутника, тоді 26х (см²) – початкова площа прямокутника. Після збільшення маємо х + 4 (см) – нова довжина прямокутника, тоді  26 (х + 4) (см²) – нова площа прямокутника. Знайдемо різницю між новою площею і початковою.

26 (х + 4) – 26 х = 26 х + 104 – 26 х = 104 (см²) – на стільки збільшиться площа прямокутника.

Відповідь: площа прямокутника збільшиться на 104 см².

 

Вправа 619 Довжина прямокутника дорівнює 32 см. На скільки квадратних сантиметрів зменшиться площа цього прямокутника, якщо його ширину зменшити на 5 см?

Розв’язання

Нехай х (см) – ширина прямокутника, тоді 32х (см²) – площа прямокутника. Після зменшення х – 5 (см) – нова ширина прямокутника, тоді 32 (х – 5) (см²) – нова площа прямокутника. Знайдемо різницю між новою площею і початковою.

32х – 32 (х – 5) = 32х – 32х + 32 • 5 = 160 (см²) – на стільки зменшиться площа прямокутника.

Відповідь: площа прямокутника зменшиться на 160 см².

 

Вправа 620 У скільки разів збільшаться периметр і площа прямокутника, якщо кожну його сторону збільшити в 4 рази?

Розв’язання

Периметр прямокутника: (а + b) • 2 = 2а + 2b

Периметр прямокутника, коли кожну сторону збільшити в 4 рази:

(4а + 4b) • 2 = 8a + 8b = 4(2a + 2b)

Отже, периметр збільшиться у 4 рази.

Площа прямокутника: аb

Пплоша прямокутника, коли кожну сторону збільшити в 4 рази:

4а • 4b = 16 аb

Отже, площа прямокутника збільшиться у 16 разів.

  

Вправа 621 У скільки разів зменшаться периметр і площа прямокутника, якщо кожну його сторону зменшити в 3 рази?

Розв’язання

Периметр прямокутника: (а + b) • 2 = 2а + 2b

Периметр прямокутника, коли кожну сторону зменшити в 3 рази:

(а/3 + b/3) • 2 = 2/3 (a + b) = 2(a + b):3

Отже, периметр зменшиться у 3 рази.

Площа прямокутника: аb

Пплоша прямокутника, коли кожну сторону збільшити в 4 рази:

а/3 • b/3 = аb/9 = аb : 9

Отже, площа прямокутника зменшиться у 9 разів.

 

Вправа 622 Вважаючи, що довжина сторони клітинки дорівнює 1 см, знайдіть площі фігур, зображених на рисунку 161.

1 см = 10 мм

а) 100 • 3 + 50 • 3 = 300 + 150 = 450 мм²

б) 100 • 3 + 50 • 4 = 300 + 200 = 500 мм² = 5 см²

в) 100 • 8 + 50 • 6 = 800 + 300 = 1100 мм² = 11 см²

г) 100 • 6 + 50 • 12 = 600 + 600 = 1200 мм² = 12 см²

 

Вправа 623 Вважаючи, що довжина сторони клітинки дорівнює 1 см, знайдіть площі фігур, зображених на рисунку 162.

1 см = 10 мм

а) 100 • 2 + 50 • 4 = 200 + 200 = 400 мм² = 4 см²

б) 100 • 6 + 50 • 6 = 600 + 300 = 900 мм² = 9 см²

в) 100 • 4 + 50 • 8 = 400 + 400 = 800 мм² = 8 см²

г) 100 • 4 + 50 • 8 = 400 + 400 = 800 мм² = 8 см²

 

Вправа 626 Довжина кожної зі сторін прямокутного аркуша паперу дорівнює цілому числу сантиметрів, а площа аркуша — 12 см². Скільки квадратів площею 4 см² можна вирізати із цього прямокутника?

12 см² = 1 см • 12 см, не можна вирізати квадрат зі стороною 2 см.

12 см² = 4 см • 3 см, можна вирізати 1 квадрат зі стороною 2 см.

12 см² = 2 см • 6 см, можна вирізати 3 квадрати зі стороною 2 см.

Відповідь: з аркуша розмірами 4 см х 3 см можна вирізати один квадрат зі стороною 2 см, а з аркуша розмірами 2 см х 6 см - два квадрати зі стороною 2 см.

 

Вправи для повторення

Вправа 627 Із вершини прямого кута ABC провели промені BD і BE так, що кут АВЕ більший за кут DBE на 34°, а кут CBD більший за кут DBE на 23°. Яка градусна міра кута DBE?

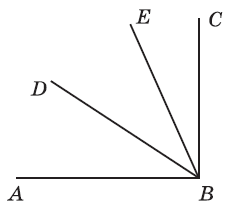
Розв’язання

<АВЕ – <DBE = <АВD = 34°

<СВD – <DВЕ = <СВЕ = 23°

<DВЕ = <АВС – <АВD – <СВЕ = 90° – 34° – 23° = 33°

 

Вправа 628 Порядок дій

1) 1008 • 604 – 105 984 : 12 – 54 321 = 545679
х  1008      604    4032 6048     608832	_105984 | 12      96         8832   _99     96     _38       36       _24         24           0	_608832      8832   600000	_600000    54321  545679
2) (57 • 34 + 812 754 : 27) : 18 = 1780
х   57     34   228 171   1938	_812754 | 27     81          30102    _2      0     _27       27         _54           54             0	+30102    1938   32040	_32040 | 18      18         1780 _140   126   _144     144        0

УЧИМОСЯ ЗАСТОСОВУВАТИ МАТЕМАТИКУ

Вправа 629 Чи вистачить фермерці Поліні Працелюб 5 т гороху, щоб засіяти ним поле, яке має форму прямокутника зі сторонами 500 м і 400 м, якщо на 1 га землі треба висіяти 260 кг гороху?

Розв’язання

1) 500 • 400 = 200000 (м²) = 20 (га) – площа поля.

2) 260 • 20 = 5200 (кг) = 5 т 200 кг – гороху необхідно.

5 т < 5 т 200 кг

Відповідь: не вистачить.

 

Вправа 630 Батько вирішив обкласти кахлем стіну кухні, довжина якої дорівнює 4 м 50 см, а висота — 3 м. Чи вистачить йому 15 ящиків кахлю, якщо одна плитка має форму квадрата зі стороною 15 см, а в одному ящику міститься 40 плиток?

Розв’язання

4 м 50 см = 450 см

3 м = 300 см

1) 450 • 300 = 135000 (см²) – площа стіни.

2) 15 • 15 = 225 (см²) – площа плитки.

3) 135000 : 225 = 600 (п.) – треба плиток.

4) 40 • 15 = 600 (п) – плиток у 15 ящиках.

Відповідь: вистачить кахлю.

 

Вправа  631 Витрати емалевої фарби на одношарове покриття становлять 180 г на 1 м². Чи вистачить 3 кг емалі, щоб пофарбувати стіну довжиною 6 м і висотою 3 м?

Розв’язання

1) S = 6 м • 3 м = 18 (м²) – площа стіни.

2) 180 • 18 = 3240 (г) = 3 кг 240 г – фарби треба для фарбування стіни.

3 кг < 3 кг 240 г

Відповідь: не вистачить фарби.

 

Задача від Мудрої Сови

Завдання 632 На озері почали розпускатися лілії. Кожного дня площа поверхні озера, зайнята ліліями, збільшувалась удвічі. На двадцятий день ліліями заросла вся поверхня озера. На який день половина озера була вкрита ліліями? 

Розв’язання

Оскільки площа збільшувалась вдвічі, тоді, якщо на 20 день поверхня озера заросла, то попереднього дня була вкрита половина озера.

Відповідь: на 19 день була вкрита ліліями половина озера.   

 

------------------------------------ у підручнику за 2018 рік -----------------------------

Питання

2. Що роблять, коли хочуть виміряти якусь величину? Вводять одиницю вимірювання.

8. Чи правильно, що коли площі фігур рівні, то рівні й самі фігури? Ні, наприклад, 64 см² = 8 см • 8 см = 2 см • 32 см, тобто однакову площу мають різні фігури. 

 

Вправа 582 Виразіть:

1) в арах: 14 га 68 а; 123 800 м²; 4 км² 72 га 16 а;

14 га 68 а = 1468 а

123800 м² = 1238 а

4 км² 72 га 16 а = 47216 а

2) у квадратних метрах: 5 а; 63 га; 14 га 43 а;

5а =  500 м²

63 га = 630000 м²

14 га 43 а = 144300 м²

3) у гектарах і арах: 85 200 м².

Розв’язання. 

85200 м² = 852 а = 8 га 52 а

 

Вправа 583 Виразіть:

1) у квадратних сантиметрах: 8 дм²; 38 м²; 74 м² 3 дм²;

8 дм² = 800 см²

38 м² = 380000 см²

74 м² 3 дм² = 740300 см²

2) у гектарах: 53 км²; 24 км² 6 га.

53 км² = 5300 га

24 км² 6 га = 2406 га

 

Вправа 588* Чи вистачить 5 т гороху, щоб засіяти ним поле, яке має форму прямокутника зі сторонами 500 м і 400 м, якщо на 1 га землі треба висіяти 260 кг гороху? 

Розв’язання

1) 500 • 400 = 200000 (м²) = 20 (га) – площа поля.

2) 260 • 20 = 5200 (кг) = 5 т 200 кг – треба гороху.

Відповідь: не вистачить.

 

Вправа 590* Фермер Петро Працелюб посіяв огірки в теплиці, довжина якої дорівнює 16 м 50 см, а ширина — 12 м. Скільки кілограмів огірків збере фермер у своїй теплиці, якщо з 1 м² збирають З0 кг огірків?

Розв’язання

1) 1650 см • 1200 см = 1980000 см² = 198 (м²) – площа

2) 30 • 198 = 5940 (кг)

Відповідь: фермер збере 5940 кг огірків.

 

Вправа 597* Площа квадрата ABCD дорівнює 16 см². Чому дорівнює площа прямокутника ACFE?

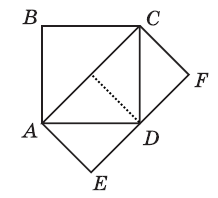
Розв’язання

1) 16 : 2 = 8 (см²)

2) 2 • 8 см² = 16 см²  

Відповідь: площа прямокутника дорівнює площі квадрата.

 

Вправа 599' Довжина кожної зі сторін прямокутного аркуша паперу дорівнює цілому числу сантиметрів, а площа аркуша — 18 см². Скільки квадратів зі стороною 3 см можна вирізати із цього аркуша?

18 см² = 1 см • 18 см, не можна вирізати квадрат зі стороною 3 см.

18 см² = 9 см • 2 см, не можна вирізати квадрат зі стороною 3 см.

18 см² = 6 см • 3 см, можна вирізати 2 квадрати зі стороною 3 см.

Відповідь: з аркуша розмірами 6 см х 3 см можна вирізати два квадрати зі стороною 3 см.

 

Вправа 600* Усередині прямокутника ABCD вирізали отвір прямокутної форми. Як одним прямолінійним розрізом поділити отриману фігуру на дві фігури, що мають рівні площі?

Розв’язання

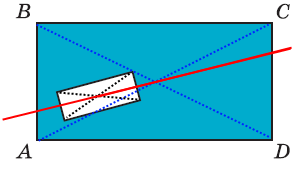
Лінія розрізу повиння проходити через точки, що є точками перетину діагоналей прямокутників. 

 

Вправа 601* Використовуючи чотири з п’яти зображених на рисунку 151 фігур, складіть квадрат.

Розв’язання

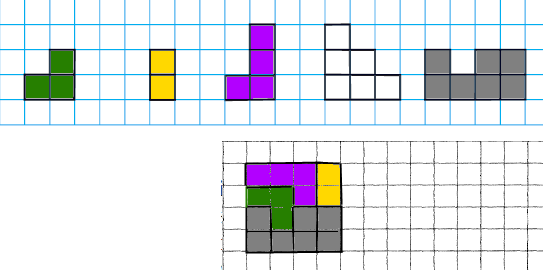
Вправа 602* Чи можна розрізати квадрат на кілька частин так, щоб з них можна було скласти два квадрати, довжини сторін яких дорівнюють цілому числу сантиметрів, якщо сторона даного квадрата дорівнює:

1) 5 см; 2) 6 см?

Розв’язання

1) 5 см • 5 см = 25 см². оскільки число можна подати сумою квадратів

25 см² = 9 см² + 16 см², тому можна скласти два квадрати.  

2) 6 см • 6 см = 36 см², оскільки не можна подати сумою двох квадратів, значить не можна скласти два квадрати.

 

Завдання 605

Назва товару	Кількість упаковок	Ціна упаковки, грн	Вартість, грн
Вафлі	84 : 7 = 12	7	84
Цукерки	5	95 : 5 = 19	305 – 126 – 84 = 95
Печиво	9	14	14 • 9 = 126
Підсумок			305

Інші завдання дивись тут ...