© ГДЗ 8next.com, 2013, 2018, 2022
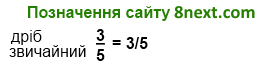
Запитання
1. Як записують звичайні дроби? Звичайні дроби записують за допомогою двох натуральних чисел і риски дробу.
2. Як називають число, записане над рискою дробу? під рискою дробу? Чисельник дробу. Знаменник дробу.
3. Що показує знаменник дробу? чисельник дробу? Знаменник дробу показує, на скільки рівних частин поділили щось ціле, а чисельник — скільки таких частин узяли.
Розвв’язуємо усно
Завдання 1 Як називають:
1) соту частину метра; сантиметр
2) тисячну частину тонни; кілограм
3) двадцять четверту частину доби; година
4) шістдесяту частину хвилини? секунда
Завдання 2 Скільки грамів:
|
1) у п’ятій частині кілограма; 1 кг : 5 = 1000 г : 5 = 200 г |
2) у десятій частині кілограма? 1 кг : 10 = 1000 г : 10 = 100 г |
Завдання 3 Скільки кілограмів:
|
1) у четвертій частині тонни; 1 т : 4 = 1000 кг : 4 = 250 кг |
2) у двадцятій частині центнера? 1 ц : 20 = 100 кг : 20 = 5 кг |
Завдання 4 Скільки секунд:
|
1) у третій частині хвилини; 1 хв : 3 = 60 с : 3 = 20 с |
2) у дев’ятій частині години; 1 год : 9 = 3600 с : 9 = 400 с |
Завдання 5 Ширина прямокутника дорівнює 8 см, що становить половину його довжини. Обчисліть периметр прямокутника.
Розв’язання
1) 8 • 2 = 16 (см) – довжина прямокутника.
2) Р = (16 см + 8 см) • 2 = 48 см – периметр прямокутника.
Відповідь: периметр прямокутника дорівнює 48 см.
Завдання 6 Знак якої арифметичної дії треба поставити замість зірочки, щоб утворилася правильна рівність:
|
1) 83 • 1 = 83 2) 2 • 2 = 4 або 2 + 2 = 4 |
3) 58 + 0 = 58 4) 34 • 0 = 0? |
Вправи
Вправа 726° Прочитайте дроби:
1/5 – одна п’ята
7/8 – сім восьмих
8/11 – вісім одинадцятих
5/16 – п’ять шістнадцятих
6/13 – шість тринадцятих
21/29 – двадцять одна двадцять дев'ята
Вправа 727° Запишіть у вигляді дробу число:
1) дві п’ятих; 2/5
2) сім тринадцятих; 7/13
3) двадцять дві шістдесятих; 22/60
4) тридцять чотири сорок третіх; 34/43
5) тридцять дев’ять сотих; 39/100
6) сто двадцять сім тисячних. 127/1000
Вправа 728° Запишіть дробом, яка частина фігури, зображеної на рисунку 199, заштрихована.
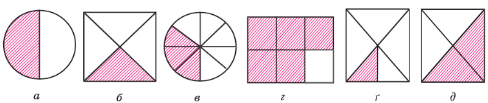
Розв’язання
а) 1/2 б) 1/4 в) 3/8 г) 5/6 ґ) 1/8 д) 2/4 або 1/2
Вправа 729° Перерисуйте фігури, зображені на рисунку 200, у зошит і зафарбуйте відповідні частини фігур.
Вправа 730° Виразіть:
1) у годинах: 1 хв; 7 хв; 39 хв; 1 с; 4 с; 58 с;
1 год = 60 хв = 3600 с
|
1 хв = 1/60 год 1 с = 1/3600 год |
7 хв = 7/60 год 4 с = 4/3600 год |
39 хв = 39/60 год 58 с = 58/3600 год |
2) у метрах: 1 см; 24 см; 1 дм; 7 дм; 1 мм; 4 мм; 39 мм.
1 м = 10 дм = 100 см = 1000 мм
|
1 см = 1/100 м 1 мм = 1/1000 м |
24 см = 24/100 м 4 мм = 4/1000 м |
1 дм = 1/10 м 39 мм = 39/1000 м |
7 дм = 7/10 м
|
Вправа 731 Виразіть у тоннах: 1 кг; 327 кг; 58 кг; 1 ц; 3 ц.
Розв’язання
1 т = 10 ц = 1000 кг
|
1 кг = 1/1000 т 3 ц = 3/10 т |
327 кг = 327/1000 т |
58 кг = 58/1000 т |
1 ц = 1/10 т
|
Вправа 732° Басейн наповнюється водою через трубу за 9 год. Яка частина басейну буде наповнена через: 1) 1 год; 2) 2 год; 3) 8 год після відкриття труби, якщо спочатку басейн був порожнім?
1) 1/9 – частина басейну буде заповнена через 1 год.
2) 2/9 – частина басейну буде заповнена через 2 год.
3) 8/9 – частина басейну буде заповнена через 8 год.
Вправа 733° Автомобіль долає відстань між двома містами за 7 год. Яку частину шляху між ними він проїде за 1 год? за 3 год? за 6 год?
1) 1/7 – частину шляху проїде за 1 год.
2) 3/7 – частину шляху проїде за 3 год.
3) 6/7 – частину шляху проїде за 6 год.
Вправа 734° У саду ростуть 56 дерев, з них 23 дерева є черешнями. Яку частину дерев становлять черешні?
23/56 – частину становлять черешні.
Вправа 735° На клумбі ростуть 32 тюльпани, із них 7 тюльпанів жовтого кольору. Яку частину всіх тюльпанів вони становлять?
7/32 – частину становлять тюльпани жовтого кольору.
Вправа 736 У книжці надруковано два оповідання. Одне оповідання займає 14 сторінок, а друге — 19 сторінок. Яку частину книжки займає кожне оповідання?
Розв’язання
1) 19 + 14 = 33 (с.) – сторінок у книжці.
2) 14/33 – частину від усіх сторінок становить перше оповідання.
3) 19/33 – частину від усіх сторінок становить друге оповідання.
Вправа 737 Марічка спекла 24 пиріжки з повидлом і 28 пиріжків з маком. Яку частину всіх пиріжків становили пиріжки з повидлом і яку частину — пиріжки з маком?
Розв’язання
1) 24 + 28 = 52 (п.) – пиріжків всього.
2) 24/52 – частину від усіх пиріжків становлять пиріжки з повидлом.
3) 28/52 – частину від усіх пиріжків становлять пиріжки з маком.
Вправа 738 Знайдіть від числа 36:
1) 1/3; 36 : 3 • 1 = 12
2) 5/6; 36 : 6 • 5 = 6 • 5 = 30
3) 5/12; 36 : 12 • 5 = 3 • 5 = 15
4) 11/18. 36 : 18 • 11 = 2 • 11 = 22
Вправа 739 Знайдіть від числа 28:
1) 1/2; 28 : 2 • 1 = 14
2) 3/7; 28 : 7 • 3 = 4 • 3 = 12
3) 9/14; 28 : 14 • 9 = 2 • 9 = 18
4) 19/28. 28 : 28 • 19 = 19
Вправа 740 Галинка прочитала 4/9 книжки, у якій 180 сторінок. Скільки сторінок прочитала Галинка?
Розв’язання
1-ий варіант запису
1) 180 : 9 = 20 (с.) – сторінок припадає на 1 частину.
2) 20 • 4 = 80 (с.) – сторінок прочитала Галинка.
2-ий варіант запису
180 : 9 • 4 = 80 (с.) – сторінок прочитала Галинка.
Відповідь: Галинка прочитала 80 сторінок.
Вправа 741 Петрик зліпив 72 вареники з м’ясом і з картоплею, причому вареники з м’ясом становили — 5/8 усіх вареників. Скільки вареників з м’ясом зробив Петрик?
Розв’язання
1-ий варіант запису
1) 72 : 8 = 9 (в.) – вареників припадає на 1 частину.
2) 9 • 5 = 45 (в.) – вареників з м’ясом зробив Петрик.
2-ий варіант запису
1) 72 : 8 • 5 = 45 (в.) – вареників з м’ясом зробив Петрик.
Відповідь: Петрик зробив 45 вареників з м’ясом.
Вправа 742 Площа одного з найкрасивіших озер України — гірського озера Синевир (Закарпаття) становить 1/3000 площі озера Сасик (Одеська область) —
найбільшого озера України. Скільки квадратних метрів становить площа озера Синевир, якщо площа озера Сасик дорівнює 210 км2?
Розв’язання
210 км2 = 210 • 1000 м • 1000 м = 210000000 м2
210000000 : 3000 = 70000 (м2) – площа озера Синевир.
Відповідь: площа озера Синевир становить 70000 м2.
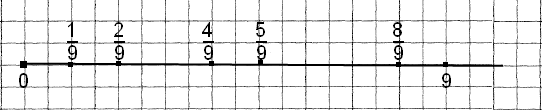
Вправа 743 Накресліть координатний промінь, одиничний відрізок якого дорівнює 9 см. Позначте на ньому точки, що відповідають дробам: 1/9; 2/9; 4/9; 5/9; 8/9.
Розв’язання
Вправа 744 Накресліть координатний промінь, одиничний відрізок якого дорівнює 12 см. Позначте на ньому точки, що відповідають дробам: 1/12; 2/12; 5/12; 6/12; 8/12; 11/12.
Розв’язання

Вправа 745 Знайдіть число, якщо: 1) 1/2; 2) 3/7; 3) 7/11; 4) 21/23 його дорівнює 42.
Якщо 42 уже становить деякий дріб, тоді
|
1) 42 : 1 • 2 = 84 2) 42 : 3 • 7 = 14 • 7= 98 |
3) 42 : 7 • 11 = 6 • 11= 66 4) 42 : 21 • 23 = 2 • 23 = 46 |
Вправа 746° Знайдіть число, якщо: 1) 1/9; 2) 2/9; 3) 3/10; 4) 5/6 його дорівнює 90.
Розв’язання
Якщо 90 уже становить деякий дріб, тоді
|
1) 90 : 1 • 9 = 810 2) 90 : 2 • 9 = 45 • 9 = 405 |
3) 90 : 3 • 10 = 30 • 10= 300 4) 90 : 5 • 6 = (50 + 40) : 5 • 6 = 108 |
Вправа 747 У саду ростуть 24 вишні, що становить 2/9 усіх дерев саду. Скільки всього дерев росте в саду?
Розв’язання
Якщо 24 вишні уже становить дріб 2/9, тоді
24 : 2 • 9 = 108 (д.) – дерев у саду.
Відповідь: у саду росте всього 108 дерев.
Вправа 748 За контрольну роботу з математики оцінку «9» одержали 12 учнів, що становить 4/11 учнів класу. Скільки учнів у цьому класі?
Розв’язання
Якщо 12 учнів уже становить дріб 4/11 від учнів класу, тоді
12 : 4 • 11 = 33 (уч.) – учнів у цьому класі.
Відповідь: у цьому класі 33 учні.
Вправа 749 Яку частину площа зафарбованого трикутника (рис. 201) становить від площі:
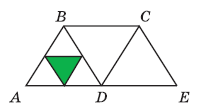
1) трикутника ABD;
1/4 (усього 4 трикутники, зафарбований один трикутник)
2) чотирикутника ABCD;
1/8 (усього 4 • 2 = 8 трикутників, зафарбований один трикутник)
3) чотирикутника АВСЕ?
1/12 (усього 4 • 3 = 12 трикутників, зафарбований один трикутник).
Вправа 750 Сторона квадрата ABCD дорівнює 8 см (рис. 202). Знайдіть загальну площу зафарбованих частин квадрата.
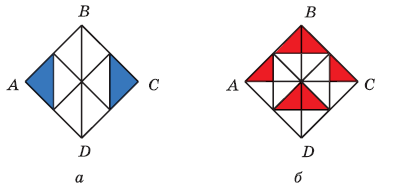
а) Розв’язання
1) 8 • 8 = 64 (см2) – площа квадрата.
Оскільки зафарбована частина становить 2/8 від площі квадрата, тому
2) 64 : 8 • 2 = 16 (см2) – площа зафарбованих частин квадрата.
Відповідь: загальна площа зафарбованих частин квадрата 16 см2.
б) Розв’язання
1) 8 • 8 = 64 (см2) – площа квадрата.
Оскільки зафарбована частина становить 6/16 від площі квадрата, тому
2) 64 : 16 • 6 = 24 (см2) – площа зафарбованих частин квадрата.
Відповідь: загальна площа зафарбованих частин квадрата 24 см2.
Вправа 751 Сторона квадрата ABCD дорівнює 4 см (рис. 203). Знайдіть загальну площу зафарбованих частин квадрата.
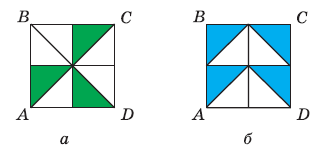
Розв’язання
а)
1) 4 • 4 = 16 (см2) – площа квадрата.
Оскільки зафарбована частина становить 3/8 від площі квадрата, тому
2) 16 : 8 • 3 = 6 (см2) – площа зафарбованих частин квадрата.
Відповідь: загальна площа зафарбованих частин квадрата 6 см2.
б)
1) 4 • 4 = 16 (см2) – площа квадрата.
Оскільки зафарбована частина становить 4/8 від площі квадрата, тому
2) 16 : 8 • 4 = 8 (см2) – площа зафарбованих частин квадрата.
Відповідь: загальна площа зафарбованих частин квадрата 8 см2.
Вправа 752 Скільки градусів становлять:
1) 2/15 величини прямого кута;
Оскільки величина прямого кута дорівнює 90°, тому
90° : 15 • 2 = 6° • 2 = 12°
2) 11/20 величини розгорнутого кута?
Оскільки величина розгорнутого кута дорівнює 180°, тому
180° : 20 • 11 = 9° • 11 = 99°
Вправа 753 Накресліть за допомогою транспортира кут, величина якого становить:
1) 7/18 величини прямого кута;
Оскільки величина прямого кута дорівнює 90°, тому
90° : 18 • 7 = 90° : 9 : 2 • 7 = 5° • 7 = 35° – треба накреслити кут.
2) 5/12 величини розгорнутого кута?
Оскільки величина розгорнутого кута дорівнює 180°, тому
180° : 12 • 5 = 180° : 6 : 2 • 5 = 30° : 2 • 5 = 75° – треба накреслити кут.
Вправа 754 Три рибалки зловили 168 риб. Щукін зловив 5/14 усіх риб, Окунєв — 8/21 усіх риб, а Карасьов — решту. Скільки риб зловив Карасьов?
Короткий запис
Усіх — 168 риб
Щукін зловив — ?, 5/14 усіх риб
Окунєв — ?, 8/21 усіх риб
Карасьов — ?, решту
Розв’язання
1) 168 : 14 • 5 = 12 • 5 = 60 (р.) – риб зловив Щукін.
2) 168 : 21 • 8 = 8 • 8 = 64 (р.) – риб зловив Окунєв.
3) 60 + 64 = 124 (р.) – риб зловили Щукін та Окунєв разом.
4) 168 – 124 = 44 (р.) – риб зловив Карасьов.
Відповідь: Карасьов зловив 44 риби.
Вправа 755 За чотири дні яхта капітана Врунгеля «Біда» пройшла 624 км. За перший день було пройдено 2/13 усієї відстані, за другий — 5/26 , за третій — 5/12 , а за четвертий — решту. Скільки кілометрів пройшла яхта за четвертий день?
Короткий запис
Уся відстань — 624 км
I — ?, 2/13 усієї відстані
II — ?, 5/26 усієї відстані
III — ?, 5/12 усієї відстані
IV — ?, решту
Розв’язання
1) 624 : 13 • 2 = 48 • 2 = 96 (км) – пройшла відстань за перший день.
2) 624 : 26 • 5 = 24 • 5 = 120 (км) – пройшла відстань за другий день.
3) 624 : 12 • 5 = 52 • 5 = 260 (км) – пройшла відстань за третій день.
4) 96 + 120 + 260 = 476 (км) – пройшла відстань за три дні разом.
5) 624 – 476 = 148 (км) – пройшла відстань за четвертий день.
Відповідь: за четвертий день яхта пройшла 148 км.
Вправа 756 Лисиця Аліса подарував Коту в чоботях 9 кг 450 г сметани. За перший тиждень Кіт у чоботях з’їв 8/21 подарунка, а за другий тиждень — 9/13 решти. Скільки сметани з’їв Кіт у чоботях за другий тиждень?
Короткий запис
Подарунок — 9 кг 450 г
I — ?, 8/21 подарунка
II — ?, 9/13 решти
Розв’язання
9 кг 450 г = 9450 г
1) 9450 : 21 • 8 = 450 • 8 = 3600 (г) – сметани з'їв за перший тиждень.
2) 9450 – 3600 = 5850 (г) – решта сметани.
3) 5850 : 13 • 9 = 450 • 9 = 4050 (г) = 4 кг 50 г – сметани з'їв за другий тиждень.
Відповідь: Кіт у чоботях за другий тиждень з'їв 4 кг 50 г сметани.
Вправа 757 Ілля Муромець заготував на зиму для свого коня 4 т 9 ц вівса. За грудень кінь з’їв 3/7 усього запасу вівса, а за січень 9/14 решти. Скільки центнерів вівса кінь з’їв за січень?
Короткий запис
Запас вівса — 4 т 9 ц
За грудень — ?, 3/7 запасу вівса
За січень — ?, 9/14 решти
Розв’язання
4 т 9 ц = 40 ц + 9 ц = 49 ц
1) 49 : 7 • 3 = 21 (ц) – вівса з'їв за грудень.
2) 49 – 21 = 28 (ц) – решта вівса.
3) 28 : 14 • 9 = 18 (ц) = 1 т 8 ц – вівса з'їв за січень.
Відповідь: за січень кінь з'їв 1 т 8 ц вівса.
Вправа 758 Фермери Іван, Назар і Тарас виростили разом 612 т ячменю та поділили врожай між собою. Івану дісталося 5/17 усього врожаю, Назару — 9/16 решти. Скільки тонн ячменю отримав Тарас?
Короткий запис
Усього врожаю — 612 т
Іванові — ?, 5/17 уього врожаю
Назару — ?, 9/16 решти
Тарасу — ?
Розв’язання
1) 612 : 17 • 5 = 36 • 5 = 180 (т) – ячменю дісталось Івану.
2) 612 – 180 = 432 (т) – решта ячменю (дісталось Назару та Тарасу).
3) 432 : 16 • 9 = 27 • 9 = 243 (т) – ячменю дісталося Назару.
4) 432 – 243 = 189 (т) – ячменю дісталося Тарасу.
Відповідь: Тарас отримав 189 т ячменю.
Вправа 759 Чебурашка, крокодил Гена й мадам Шапокляк поїхали у Херсон на збирання кавунів. Разом вони заробили 1024 грн і розділили їх відповідно до того, хто як працював. Чебурашка одержав 11/32 зароблених грошей, крокодил Гена — 5/8 решти. Хто з цієї компанії найпрацьовитіший?
Короткий запис
Заробили грошей — 1024 грн
Чебурашка — ?, 11/32 зароблених грошей
Гена — ?, 5/8 решти
Шапокляк — ?
Розв’язання
1) 1024 : 32 • 11 = 32 • 11 = 352 (грн) – грошей одержав Чебурашка.
2) 1024 – 352 = 672 (грн) – решта грошей (одержав крокодил Гена і Шапокляк).
3) 672 : 8 • 5 = 84 • 5 = 420 (грн) – грошей одержав крокодил Гена.
4) 672 – 420 = 252 (грн) – грошей отримала Шапокляк.
Відповідь: найпрацьовитіший крокодил Гена.
Вправа 760 До дитячого санаторію завезли банани, апельсини та мандарини. Маса апельсинів становить 12/35 маси бананів, а маса мандаринів — 7/12 маси апельсинів. Скільки кілограмів апельсинів і мандаринів разом завезли до санаторію, якщо бананів завезли 245 кг?
Короткий запис
Банани — 245 кг
Апельсини — ?, 12/35 маси бананів
Мандарини — ?, 7/12 маси апельсинів
Апельсинів і мандаринів — ?
Розв’язання
1) 245 : 35 • 12 = 7 • 12 = 84 (кг) – маса апельсинів.
2) 84 : 12 • 7 = 7 • 7 = 49 (кг) – маса мандаринів.
3) 84 + 49 = 133 (кг) – маса апельсинів та мандаринів разом.
Відповідь: до санаторію завезли 133 кг апельсинів та мандаринів.
Вправа 761 Подорожуючи на човні Дніпром, Софія за перший тиждень проплила 72 км, за другий тиждень — 7/8 того, що проплила за перший тиждень, а за третій — 8/9 того, що проплила за другий. На скільки кілометрів менше проплила Софія за третій тиждень, ніж за другий?
Короткий запис
I — 72 км
II — ?, 7/8 того, що за I
III — ?, 8/9 того, що II
На скільки менше — ?
Розв’язання
1) 72 : 8 • 7 = 9 • 7 = 63 (км) – проплила за другий тиждень.
2) 63 : 9 • 8 = 7 • 8 = 56 (км) – проплила за третій тиждень.
3) 63 – 56 = 7 (км) – на стільки менше проплила за третій тиждень, ніж за другий.
Відповідь: за третій тиждень Софія проплила на 7 км менше, ніж за другий тиждень.
Вправа 762 Знайдіть число, 2/3 якого дорівнюють З/7 числа 210.
Розв’язання
1) 210 : 7 • 3 = 90 – деяке число (3/7 частини від 210).
Якщо 90 – деяке число, що вже становить дріб 2/3, тоді
2) 90 : 2 • 3 = 135 – шукане число.
Відповідь: шукане число 135.
Вправа 763 Знайдіть 5/8 числа, 5/12 якого дорівнюють 160.
Розв’язання
Якщо 160 уже становить дріб 5/12 від деякого числа, тоді
1) 160 : 5 • 12 = 32 • 12 = 384 – деяке число.
2) 384 : 8 • 5 = 48 • 5 = 240 – шукане число (5/8 частин від деякого числа).
Відповідь: шукане число 240.
Вправа 764 Один із доданків дорівнює 324 і становить 12/25 суми. Знайдіть другий доданок.
Розв’язання
Якщо доданок 324 уже становить дріб 12/25 від суми, тоді
1) 324 : 12 • 25 = 27 • 25 = 675 – сума.
2) 675 – 324 = 351 – другий доданок.
Відповідь: другий доданок дорівнює 351.
Вправа 765 Знайдіть різницю двох чисел, якщо від’ємник дорівнює 658 і становить 7/15 зменшуваного.
Розв’язання
Якщо від’ємник 658 уже становить дріб 7/15 від зменшуваного, тоді
1) 658 : 7 • 15 = 94 • 15 = 1410 – зменшуване.
2) 1410 – 658 = 752 – різниця.
Відповідь: різниця двох чисел дорівнює 752.
Вправа 766 Маса діжки з водою дорівнює 60 кг. Коли з діжки вилили четверту частину води, то маса діжки з водою, що залишилася, склала 50 кг. Яка маса пустої діжки?
Розв’язання
1) 60 – 50 = 10 (кг) – четверта частина води, що вилили.
2) 10 • 4 = 40 (кг) – маса води.
3) 60 – 40 = 20 (кг) – маса порожньої діжки.
Відповідь: маса порожньої діжки 20 кг.
Вправи для повторення.
Вправа 767 Розв’яжіть рівняння
|
1) 9х – 4х + 39 = 94 5х + 39 = 94 5х = 94 – 39 5х = 55 х = 55 : 5 х = 11
|
2) 7у + 2у – 34 = 83. 9у – 34 = 83 9у = 83 + 34 9 у = 117 у = 117 : 9 у = (90 + 27) : 9 у = 13 |
Вправа 768 Із двох яблунь Івасик-Телесик зібрав 65 кг яблук, причому з однієї яблуні він зібрав на 17 кг менше, ніж із другої. Скільки кілограмів яблук він зібрав з кожної яблуні?
Розв’язання
1 спосіб
Нехай х (кг) – яблук зібрав з першої яблуні, тоді х + 17 (кг) – яблук зібрав з другої яблуні. Складемо рівняння
х + (х + 17) = 65
2х + 17 = 65
2х = 65 – 17
2х = 48
х = 48 : 2
х = 24 (кг) – яблук зібрав з першої яблуні.
х + 17 = 24 + 17 = 41 (кг) – яблук зібрав з другої яблуні.
2 спосіб
1) 65 – 17 = 48 (кг) – зібрав порівну.
2) 48 : 2 = 24 (кг) – зібрав з одної яблуні.
3) 24 + 17 = 41 (кг) – зібрав з другої яблуні.
Відповідь: з першої яблуні Івасик-Телесик зібрав 24 кг яблук, з другої – 41 кг яблук.
Вправа 769 Відстань між двома селами дорівнює 28 км. Із цих сіл одночасно в одному напрямку виїхали мотоцикліст і автобус. Автобус їхав попереду зі швидкістю 42 км/год, а мотоцикліст їхав зі швидкістю 56 км/год. Через скільки годин після початку руху мотоцикліст наздогнав автобус?
Розв’язання
1) 56 – 42 = 14 (км/год) – швидкість зближення.
2) 28 : 14 = 2 (год) – час зустрічі.
Відповідь: через 2 год після початку руху мотоцикліст наздогнав автобус.
Задача від Мудрої Сови
Вправа 722 До п’яти різних замків є п’ять ключів, причому невідомо, який ключ до якого замка підходить. Барон Мюнхгаузен стверджує, що можна не більше ніж за 10 спроб підібрати ключ до кожного замка. Чи правий барон Мюнхгаузен?
Розв’язання
До першого замка ключ можна підібрати щонайбільше за 4 спроби. Якщо до першого замка не підійшов жоден з чотирьох ключів, то обов'язково підійде п'ятий.
Залишається чотири ключі.
До другого замка підібрати ключ можна за 3 спроби. Якщо до другого замка не підійшов жоден з трьох ключів, то обов'язково підійде четвертий.
Залишається три ключі.
До третього замка підібрати ключ можна за 2 спроби. Якщо до третього замка не підійшов жоден з двох ключів, то обов'язково підійде третій.
Залишається 2 ключі.
До четвертого замка підібрати ключ можна за 1 спробу. Якщо до четвертого замка не підійшов той ключ, то обов'язково підійде другий.
Залишився 1 ключ, він обов'язково підійде до п’ятого замка.
Ключ до кожного замка можна підібрати щонайменше за 4 + 3 + 2 + 1 = 10 спроб.
Відповідь: барон Мюнхгаузен правий.
------------------------- у підручниках 2013, 2018 років ------------------
Завдання 3 Скільки секунд:
2) у дванадцятій частині хвилини;
1 хв : 12 = 60 с : 12= 5 с
4) у тридцятій частині години?
1 год : 30 = 3600 с : 30 = 120 с
Завдання 6 Обчисліть:
1) суму частки чисел 72 і 9 та числа 22;
72 : 9 + 22 = 8 + 22 = 30
2) різницю числа 60 та частки чисел 126 і 6;
60 – 126 : 6 = 60 – 21 = 39
3) добуток частки чисел 714 і 7 та числа 0.
714 : 7 • 0 = 0
Вправа 684° Виразіть:
1) у метрах: 5 см; 39 мм; 247 мм;
Оскільки 1 м = 10 дм = 100 см = 1000 мм, маємо
5 см = 5/100 м
39 мм = 39/1000 м
247 мм = 247/1000 м
2) у годинах: 19 хв.
оскільки 1 год = 60 хв = 3600 с, маємо
19 хв = 19/60 год
Вправа 687 У 5 класі 32 учні, з них 7 учнів написали контрольну роботу з математики на 12 балів. Яку частину учнів класу вони становлять?
7/32 – частина учнів класу, котрі написали контрольну роботу з математики на 12 балів.
Вправа 690 Знайдіть від числа 36:
2) 3/4; 4) 4/9
Розв’язання
2) 36 : 4 • 3 = 9 • 3 = 27
4) 36 : 9 • 4 = 4 • 4 = 16
Вправа 692 Петрик прочитав 4/9 книжки, у якій 180 сторінок. Скільки сторінок прочитав Петрик?
Розв’язання
180 : 9 • 4 = 80 (с.) – сторінок прочитав Петрик.
Відповідь: Петрик прочитав 80 сторінок.
Вправа 693 Галинка зліпила 72 вареники з м’ясом і з картоплею, причому вареники з м’ясом становили — 5/8 усіх вареників. Скільки вареників з м’ясом зробила Галинка?
Розв’язання
72 : 8 • 5 = 45 (в.) – вареників з м’ясом зробила Галинка.
Відповідь: Галинка зробила 45 вареників з м’ясом.
Вправа 695° Знайдіть число, якщо: 1) 1/2; 2) 1/5; 3) 2/3; 4) 3/7; 5) 7/11; 6) 21/23 його дорівнює 42.
Розв’язання
Якщо 42 уже становить деякий дріб, тоді
1) 42 : 1 • 2 = 84
2) 42 : 1 • 5 = 210
3) 42 : 2 • 3 = 21 • 3= 63
4) 42 : 3 • 7 = 14 • 7= 98
5) 42 : 7 • 11 = 6 • 11= 66
6) 42 : 21 • 23 = 2 • 23 = 46
Вправа 696 Знайдіть число, якщо: 1) 1/9; 2) 2/5; 3) 2/9; 4) 3/10; 5) 5/6; 6) 18/19 його дорівнює 90.
Розв’язання
Якщо 90 уже становить деякий дріб, тоді
1) 90 : 1 • 9 = 810
2) 90 : 2 • 5 = 45 • 5 = 225
3) 90 : 2 • 9 = 45 • 9 = 405
4) 90 : 3 • 10 = 30 • 10= 300
5) 90 : 5 • 6 = (50 + 40) : 5 • 6 = 108
6) 90 : 18 • 19 = 90 : 9 : 2 • 19 = 5 • 19 = 95
Вправа 714* Із двох портів, відстань між якими дорівнює 576 миль, одночасно назустріч один одному вийшли кораблі капітана Врунгеля і Сіндбада-мореплавця. Яхта капітана Врунгеля проходила за день 42 милі, що становить — 7/9 того, що проходив за день корабель Сіндбада. Через скільки днів після початку руху зустрілися мореплавці?
Розв’язання
Якщо 42 милі уже становить дріб 7/9 відстані Синдбада за день, тоді
1) 42 : 7 • 9 = 54 (км) – відстань корабля Сіндбада за 1 день.
2) 42 + 54 = 96 (км) – відстань проходили за 1 день два кораблі разом.
3) 576 : 96 = 6 (днів) – час зустрічі.
Відповідь: кораблі зустрінуться через 6 днів.
Вправа 715 3 Квіткового та Сонячного міст виїхали одночасно назустріч один одному Знайко і Незнайко. Знайко їхав зі швидкістю 56 км/год, що становило 8/11 швидкості руху Незнайка. Через скільки годин після початку руху вони зустрілися, якщо відстань між містами дорівнює 532 км?
Розв’язання
Якщо 56 км/год уже становить дріб 8/11 від швидкості руху Незнайка, тоді
1) 56 : 8 • 11 = 77 (км/год) – швидкість руху Незнайка.
2) 56 + 77 = 133 (км/год) – швидкість зближення.
3) 532 : 133 = 4 (год) – час зустрічі.
Відповідь: вони зустрілися через 4 год від початку руху.