ЗАВДАННЯ № 4 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ

Завдання 1
Колоду розпилили на дві колоди завдовжки 3 м і 4 м. Яку частину даної колоди становить менша з отриманих колод?
Розв’язання.
1) 3 + 4 = 7 (м) – довжина даної колоди;
2) 3/7 м – становить менша частина колоди.
Відповідь: А) 3/7
Завдання 2. На рисунку зображено частину координатного променя. Яку координату має точка А ? Б) 2 1/4
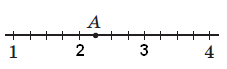
Завдання 3 Порівняння дробів
З двох дробів з однаковими знаменниками менший той, у якого менший чисельник, тому В) 7/13 < 9/13
Завдання 4
До магазину завезли 250 кг цукру. За перший день було продано 3/5 завезеного цукру. Скільки кілограмів цукру було продано за перший день?
Розв’язання
250 : 5 • 3 = 150 (кг) – цукру продано за перший день.
Відповідь: Г) 150 кг
Завдання 5
У школі навчаються 280 хлопчиків, які становлять 4/7 усіх учнів. Скільки всього учнів у цій школі?
Розв’язання
Якщо 280 хлопчиків уже становлять дріб 4/7 усіх учнів класу, тоді
1) 280 : 4 • 7 = 490 (уч.) – учнів у класі.
Відповідь: А) 490
Завдання 6 Перетворення дробів
Перетворіть у мішане число дріб 49/11
_49 | 11
44 4 (ост. 5)
5
49/11 = 4 5/11, тому Б) 4 5/11
Завдання 7
Подайте у вигляді неправильного дробу число 4 5/12
Знайдемо чисельник дробу 4 • 12 + 5 = 48 + 5 = 53, маємо дріб 53/12, тому Б 53/12
Завдання 8 Віднімання дробів
9 – 5 2/7 = 8 7/7 – 5 2/7 = 3 5/7, тому Г) 3 5/7
Завдання 9
Чому дорівнює найменше натуральне значення m, при якому є правильною нерівність m > 35/6
Зведемо дріб 35/6 до мішаного дробу.
_35 | 6
30 5 (ост. 5)
5
Маємо мішаний дріб 5 5/6, тобто 35/6 = 5 5/6, маємо m > 5 5/6, m = 6, тому В) 6
Завдання 10 Додавання дробів
Яке число має стояти в кінці ланцюжка обчислень?

1) 6 3/11 + 1 2/11 = (6 + 1) + (3/11 + 2/11) = 7 + 5/11 = 7 5/11
2) 7 5/11 – 4 8/11 = 6 16/11 – 4 8/11 = 2 8/11
3) 2 8/11 + 3 3/11 = 5 11/11 = 6, тому А) 6
Завдання 11
При якому найбільшому натуральному знаечнні m дріб 30/(5m+10) буде неправильним?
Якщо чисельник більший або рівний знаменнику, тоді дріб називається неправильним.
30 ≥ 5m + 10
20 + 10 ≥ 5m + 10
20 ≥ 5m
5 • 4 ≥ 5m
4 ≥ m , для m = 1, 2, 3, 4.
Найбільше натуральне значення m дорівнює 4, тому Б) 4
Завдання 12
Укажіть усі натуральному значення а, при яких кожний із дробів а/7 і 4/а буде правильним.
Якщо чисельник менший за знаменник, тоді дріб називається правильним.
Маємо дві нерівності а < 7 та 4 < а, отримаємо подвійну нерівність 4 < а < 7.
При а = 5, 6 дроби будуть правильними, тому Б) 5; 6