Інші завдання дивись тут...

Завдання 346

Розрядні одиниці: 1, 10, 100

Розрядні числа: 28, 20, 50, 90, 120, 400

 

Завдання 347 Виконали дії з розрядними одиницями

3 • 1 = 3 1 • 30 = 30

8 • 10 = 80 10 • 5 = 50

20 • 10 = 200 35 • 10 = 350

6 • 100 = 600 100 • 6 = 600

14 • 10 = 140 10 • 74 = 740

б)

338 : 1 = 338 760 : 1 = 760

20 : 10 = 2 30 : 10 = 3

330 : 10 = 33 760 : 10 = 76

200 : 100 = 2 300 : 100 = 3

700 : 100 = 7 900 : 100 = 9

Завдання 348 Записали розрядні числа у вигляді добутку одноцифрового числа й розрядної одиниці

70 = 7 • 10

90 = 9 • 10

200 = 2 • 100

500 = 5 • 100

800 = 8 • 100

Завдання 349, 350 

36 • 20 = 36 • (2 • 10) = 36 • 2 • 10 = 72 • 10 = 720

18 • 40 = 18 • 4 • 10 = 64 • 10 = 640

25 • 30 = 25 • 3 • 10 = 75 • 10 = 750

4 • 200 = 4 • 2 • 100 = 8 • 100 = 800

248 : 2 = (200 + 40 + 8) : 2 = 100 + 20 + 4 = 124

 

Завдання 351 Множення числа на добуток

m • (n • a) = (m • n) • a

 

Завдання 352

На кожному із 12 поверхів будинку по 20 квартир, а на пер­шому й останньому — по 16. Скільки квартир у цьому 14–по– верховому будинку?

Розв'язання

1) 20 • 12 = 240 (кв.) – на всіх поверхах з 2-го до 13-го включно

2) 16 • 2 = 32 (кв.) – на 1-ому та 14-ому поверхах разом

3) 240 + 32 = 272 (кв.)

Відповідь: у цьому 14–поверховому будинку 272 квартири. 

 

Завдання 353 Порядок дій

248 • 3 – 19 • 20 = 364	х 248       3   744	х 19     20    380	_744   380   364	+ 647    353   1000
320 : 10 + 16 • 40 = 32 + 640 = 672	х 16     40    640	+  32   640   672
(17 • 30 – 190) : 10 = 320 : 10 = 32	х 17     30   510	_ 510   190   320
(594 : 9 + 34) • 8 = 100 • 8 = 800	_594 |  9    54     66   _54     54       0	+ 66    34  100
24 • 15 + 21 • 30 = 990	х 24   15  120  24   360	х 21     30    630	+360   630   990
903 : 3 – 444 : 4 = 190	_903 |  3     9      301    _3      3       0	_444 |  4    4     111   _4     4       4       4       0	_301    111    190

Завдання 354

У двоповерховому будинку мешкає 29 осіб, а в дев'яти­поверховому — у 30 разів більше. На скільки мешканців біль­ше в дев'ятиповерховому, ніж у двоповерховому будинку?

Розв'язання

1) 29 • 30 = 870 (ос.) – мешкають у дев'яти­поверховому будинку

2) 870 – 29 = 841 (ос.) 

Відповідь: на 841 мешканців біль­ше в дев'ятиповерховому будинку, ніж у двоповерховому. 

 

Завдання 355 Одиниці вимірювання

1 см у 100 разів коротший, ніж 1 м.

1 кг у 100 разів легший, ніж 1 ц.

1 дм у 10 разів довший, ніж 1 см.

1 дм у 100 разів довший, ніж 1 мм.

1 см у 10 разів довший, ніж 1 мм.

 

Завдання 356 

У магазин завезли 40 ящиків яблук, по 9 кг у кожному. До обіду продали 17 ящиків яблук. Скільки кілограмів яблук залишилося продати?

Розв'язання

1 спосіб

1) 9 • 40 = 450 (кг) – завезли яблук

2) 9 • 17 = 153 (кг) – продали яблук

3) 450 – 153 = 297 (кг)

2 спосіб

1) 40 – 17 = 23 (ящ.) – залишилося яблук   

2) 9 • 23 = 207 (кг)

Відповідь: залишилося продати 207 кілограмів яблук.

  

Завдання 357  Множення деяких двоцифрових чисел округлюючи множник

24 • 29 = 24 • (30 – 1) = 24 • 30 – 24 • 1 = 720 – 24 = 696

16 • 49 = 16 • (50 – 1) = 16 • 50 – 16 • 1 = 800 – 18 = 784

19 • 22 = 22 • (20 – 1) = 22 • 20 – 22 • 1 = 440 – 22 = 418

17 • 71 = 17 • (70 + 1) = 17 • 70 + 17 • 1 = 1190 + 17 = 1207

 

Завдання 358

80 : 20 = 8 : 2 = 4

120 : 20 = 12 : 2 = 6

100 : 50 = 10 : 2 = 5

140 : 70 = 14 : 7 = 2

28 • 20 = (20 + 8) • 20 = 400 + 160 = 560

17 • 40 = (10 + 7) • 40 = 400 + 280 = 680

30 • 15 = 30 • (10 + 5) = 300 + 150 = 450

50 • 12 = 50 • (10 + 2) = 500 + 100 = 600

 

Завдання 359 Ділення з остачею

84 : 20 = 4 (ост. 4)        4 • 20 + 4 = 80 + 4 = 84

93 : 30 = 3 (ост. 3)        3 • 30 + 3 = 90 + 3 = 93

85 : 40 = 2 (ост. 5)        2 • 40 + 5 = 80 + 5 = 85

68 : 30 = 2 (ост. 8)        2 • 30 + 8 = 60 + 8 = 68

120 : 50 = 2 (ост. 20)        2 • 50 + 20 = 100 + 20 = 120

65 : 20 = 3 (ост. 5)        3 • 20 + 5 = 60 + 5 = 65

109 : 20 = 5 (ост. 9)      5 • 20 + 9 = 100 + 9 = 109

47 : 20 = 2 (ост. 7)        2 • 20 + 7 = 40 + 7 = 47

 

Завдання 360 

У тебе є 720 грн двадцятигривневими купюрами. Скільки це купюр?

720 : 20 = 72 : 2 = (60 + 12) : 2 = 30 + 6 = 36 (к.)

 

Завдання 361, 362  Письмове ділення

_780 |  30    60     26  _180    180       0

_840 |  60    60     14  _240    240       0

_920 |  40    80     23  _120    120       0

х 31     20   620

Завдання 363

Для школи закупили 30 світлодіодних елек­троламп на суму 630 грн. Яка ціна однієї та­кої лампи? Скільки коштуватимуть 45 таких ламп? 10 таких ламп?

Розв'язання

1) 630 : 30 = 21 (грн) – ціна лампи

2) 21 • 40 = 945 (грн) – коштуватимуть 45 таких ламп

3) 21 • 10 = 210 (грн)

Відповідь: 45 таких ламп коштуватимуть 945 гривень, а 10 таких ламп — 210 грн.

 

Завдання 364

Звичайна електролампа (лампа розжарюван­ня) коштує 5 грн. Скільки коштують 30 таких ламп? Скільки таких ламп можна купити на 105 грн? А скільки світлодіодних?

Розв'язання

1) 5 • 30 = 150 (грн) – коштують 30 електроламп

2) 105 : 5 = 21 (л.) – можна купити таких електроламп

3) 105 : 21 = 5 (л.)

Відповідь: 30 електроламп коштують 150 гривень. За 150 грн можна купити 21 електролампу або 5 світлодіодних ламп.

 

Завдання 365

Обчисли річну економію в грошах, якщо замі­нити звичайну електролампу на світлодіодну.

Види ламп	Ціна лам­почки	Вартість спожитої електроенергії за рік	Загальні витрати	Економія
Звичайна	5 грн	715 грн	?	на ?, у ?
Світлодіодна	21 грн	59 грн	?

Розв'язання

1) 715 + 5 = 720 (грн) – загальні витрати на електролампу

2) 59 + 21 = 80 (грн) – загальні витрати на світлодіодну лампу

3) 720 – 80 = 640 (грн) – економія

4) 720 : 80 = 9 (разів)

Відповідь: економія в грошах становить 640 гривень, або в 9 разів більше, якщо замі­нити звичайну електролампу на світлодіодну.

 

Завдання 366

х 47     20   940	х 12     70   840	270 : 30 = 27 : 3 = 9	720 : 80 = 72 : 8 = 9
_940 |  20    80     47  _140    140       0	_840 |  70    70     12  _140    140       0	250 : 50 = 25 : 5 = 5	720 : 90 = 72 : 9 = 8

Завдання 367

Із 48 м тканини пошили 12 однакових костюмів. Скільки метрів тканини витратили на один костюм? На 6 костюмів?

Розв'язання

1) 48 : 12 = 4 (м) – тканини йде на 1 костюм

2) 4 • 6 = 24 (м)

Відповідь: на костюм витратили 4 метри тканини, а на 6 таких костюмів — 24 метри.

 

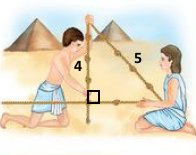
Завдання 368 

Землеміри Стародавнього Єгипту, щоб відмітити на міс­цевості прямокутну ділянку, спочатку позначали на міс­цевості прямий кут. Для цього зав'язували на однаковій відстані один від одного 13 вуз­лів на мотузці. Потім виклада­ли трикутник, який мав три проміжки між вузлами на од­ній стороні, чотири на іншій і п'ять на останній. Дві сторо­ни цього трикутника завжди утворювали прямий кут. Прямий кут був між сторонами 3 і 4 вузли.

Інші завдання дивись тут...