Якщо в задачі потрібно з'ясувати, чи паралельні прямі, то, виходячи з означення, це зробити неможливо, оскільки для цього прямі потрібно продовжити до нескінченності. Адже за означенням дві прямі на площині називають паралельними, якщо вони не перетинаються. Проте встановити, прямі паралельні чи ні, можна, використавши спеціальні теореми, які називають ознаками.
◊ Теорема (ознака паралельності прямих).
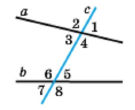
Якщо при перетині двох прямих січною відповідні кути рівні, то прямі паралельні.
Рівні пари відповідних кутів:
∠2 = ∠6;
∠3 = ∠7;
∠1 = ∠5;
∠4 = ∠8.
Наслідки з ознаки паралельності прямих
Зауважимо, що наслідки 1-3 можна також розглядати як ознаки паралельності прямих.
◊ Наслідок 1. Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні між собою, то прямі паралельні.
Рівні пари внутрішніх різносторонніх кутів:
∠3 = ∠5;
∠6 = ∠4.
◊ Наслідок 2. Якщо при перетині двох прямих січною сума внутрішніх односторонніх кутів дорівнює 180°, то прямі паралельні.
Сума внутрішніх односторонніх кутів дорівнює 180°:
∠3 + ∠6 = 180°;
∠4 + ∠5 = 180°.
◊ Наслідок 3. Дві прямі, перпендикулярні до третьої прямої, паралельні.
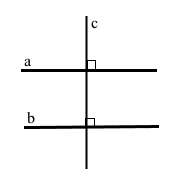
Якщо a ﬩ c і b ﬩ с, тоді a || b.