◊ Аксіома. Кожний відрізок має певну довжину, більшу за нуль.
Довжину відрізка називають також відстанню між його кінцями.
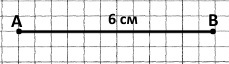
Відстанню між точками A і B називають довжину відрізка AB. Якщо точки A і B збігаються, то вважають, що відстань між ними дорівнює нулю. Пишуть AB = 6 см, кажуть «відрізок AB дорівнює 6 см», «довжина відрізка AB дорівнює 6 см».
Відстань від точки A до точки B завжди дорівнює відстані від точки B до точки A, оскільки своїми кінцями відрізок визначається однозначно. Пишемо: АВ = ВА = 6 см
Щоб виміряти довжину, треба обрати одиничний відрізок: 1 см, 1 мм тощо.
ВИМІРЮВАННЯ ВІДРІЗКІВ
◊ Аксіома вимірювання відрізків.
Основна властивість вимірювання відрізків. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його внутрішньою точкою.
![]()
Нагадаємо, що внутрішня точка – це будь-яка точка відрізку між його кінцями.
Точки A і B – кінці відрізка AB. Точка C – внутрішня точка АВ. Тоді справедлива рівність АВ = АС + СВ.
◊ Якщо точки на відрізку ділять його на частини, то довжина відрізка дорівнює сумі довжин цих частин.
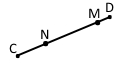
Внутрішні точки M і N ділять відрізок CD на три частини.
CD = CМ + MN + ND
◊ Якщо три точки лежать на одній прямій, то довжина більшого з трьох відрізків має дорівнювати сумі довжин двох менших.
Дане правила допомагає визначати, чи можуть три точки лежати на одній прямій.
Якщо АВ = 7 см, ВС = 3 см, АС = 9 см, тоді точки А, В, С не лежать на одній прямій, оскільки 9 см ≠ 7 см + 3 см.
Якщо АВ = 6 см, ВС = 3 см, АС = 9 см, тоді точки А, В, С можуть лежати на одній прямій, оскільки 9 см = 6 см + 3 см.
◊ Аксіома відкладання відрізка. На будь-якому промені від його початкової точки можна відкласти відрізок заданої довжини, і тільки один.
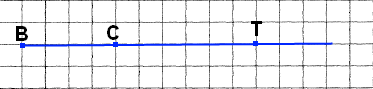
На промені ВТ можна відкласти лише один відрізок ВС заданої довжини, наприклад, ВС = 2 см.
ПОРІВНЯННЯ ВІДРІЗКІВ
◊ Два відрізки називають рівними, якщо їх можна сумістити накладанням.
◊ Два відрізки називають рівними, якщо рівні їхні довжини.
(Рівні відрізки мають рівні довжини, і навпаки, якщо довжини відрізків рівні, то рівні й самі довжини).
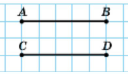
Записують: АВ = СD. Кажуть: «відрізки АВ і СD рівні».
На малюнках рівні відрізки прийнято позначати однаковою кількістю рисочок, а відрізки неоднакової довжини – різною кількістю рисочок.
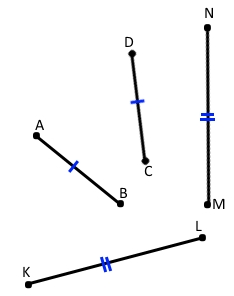
AB = CD і KL = MN.
◊ З двох відрізків більшим вважають той, довжина якого більша.

![]()
Записують: АВ > CD. Кажуть: «відрізок АВ більший за відрізок СD».
◊ З двох відрізків меншим вважають той, довжина якого менша.

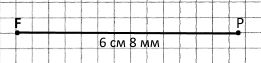
Записують: KL < FP. Кажуть: «відрізок КL менший за відрізок FP».
◊ Частина відрізка завжди має довжину, яка менша від довжини відрізка.
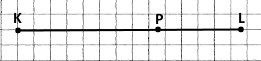
Оскільки довжини більші нуля, KP + PL = KL, тоді KP < KL , PL < KL.
◊ Якщо два відрізки рівні, то їхні половини рівні, і навпаки, якщо половини двох відрізків рівні, то й самі відрізки рівні.
Інструменти для вимірювання відрізків: лінійка, косинець, складаний метр, рулетка, клейончастий сантиметр, штангенциркуль.
