Інші завдання дивись тут...

Рівність двох трикутників можна встановити, не накладаючи один трикутник на другий, а порівнюючи лише деякі їхні еле­менти, спираючись на певні ознаки.

^{На практиці, наприклад, для встановлення рівності двох земельних ділянок трикутної форми, які не можна накласти одна на одну, зручно спиратися на ознаки.}

Ознака (у геометрії) – це теорема, яка вказує умови, вико­нання яких дає змогу стверджувати про певні властивості фігур, належність їх до певного класу тощо.

Перша ознака рівності трикутників: за двома сторонами і кутом між ними.

◊ Теорема (перша ознака рівності трикутників). Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними іншого три­кутника, то такі трикутники рівні між собою.

Якщо АВ = А₁В₁, ВС = В₁С₁, ∠В = ∠В₁, тоді можна стверджувати, що ∆АВС = ∆А₁В₁С₁

Друга ознака рівності трикутників: за стороною і двома прилеглими кутами.

◊ Теорема (друга ознака рівності трикутників). Якщо сторона і два прилеглих до неї кути одного трикутника дорівнюють відповідно стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні між собою.

Якщо АС = А₁С₁, ∠А = ∠А₁, ∠В = ∠В₁, тоді можна стверджувати, що ∆АВС = ∆А₁В₁С₁

Третя ознака рівності трикутників: за трьома сторонами.

◊ Теорема (третя ознака рівності трикутників). Якщо три сторони одного трикутника відповідно дорів­нюють трьом сторонам іншого трикутника, то такі три­кутники рівні між собою.

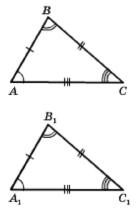
Якщо АВ = А₁В₁, ВС = В₁С₁, СD = C₁D₁, тоді можна стверджувати, що ∆АВС = ∆А₁В₁С₁

Зауважимо, що зазвичай на малюнках рівні сторони позначають однаковою кількістю рисок, а нерівні – різною кількістю рисок; рівні кути позначають однаковою кількістю дужок, а нерівні – різною кількістю дужок.

Інші завдання дивись тут...