Рівні геометричні фігури – це геометричні фігури, які можна сумістити накладанням.
Рівні відрізки – це відрізки, які можна сумістити накладанням.
Два відрізки називають рівними між собою, якщо вони мають однакову довжину.
(Рівні відрізки мають рівні довжини, і навпаки, якщо довжини відрізків рівні, то рівні й самі довжини).
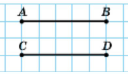
Записують: АВ = СD. Кажуть: «відрізки АВ і СD рівні».
На малюнках рівні відрізки прийнято позначати однаковою кількістю рисочок, а відрізки неоднакової довжини – різною кількістю рисочок.
◊ Якщо два відрізки рівні, то їхні половини рівні, і навпаки, якщо половини двох відрізків рівні, то й самі відрізки рівні.
Рівні кути – це кути, які можна сумістити накладанням.
◊ Два кути називають рівними між собою, якщо в них однакові градусні міри.
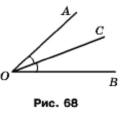
Записують: ∠AOC = ∠COB. Кажуть «кути АОС і СОВ рівні».
Якщо кути рівні, тоді їх позначають однаковою кількістю дужок при вершині, а нерівні кути – різною кількістю дужок при вершині.
◊ Якщо два кути рівні, то їхні половини рівні, і навпаки, якщо половини двох кутів рівні, то й самі кути рівні.
Рівні трикутники – це трикутники, які можна сумістити накладанням.
Сторони і кути трикутників, які суміщаються при накладанні, називають відповідними сторонами і відповідними кутами.
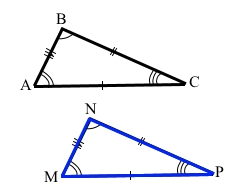
Записують ∆ABC = ∆MNP. Кажуть «трикутники ABC і MNP рівні»
Запис ∆ABC = ∆MNP означає, що відповідні сторони та кути рівні:
AB = MN, BС = NP, AC = MP;
∠A = ∠M, ∠B = ∠N, ∠C = ∠P,
Для рівних трикутників порядок запису вершин, який встановлюється рівністю відповідних кутів цих трикутників, має значення!
∆ABC ≠ ∆NPM, адже ∠A ≠ ∠N, ∠B ≠ ∠P, ∠C≠ ∠M.