Коло, описане навколо трикутника, — коло, яке проходить через всі вершини трикутника.
У такому разі трикутник називають вписаним у коло.
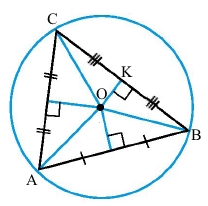
Коло з центром в точці О описане навколо трикутника АВС.
Трикутник АВС вписаний у коло з центром у точці О.
◊ Теорема (про коло, описане навколо трикутника)
Навколо будь-якого трикутника можна описати коло.
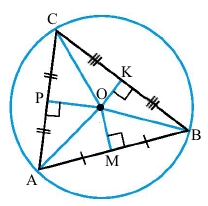
Коло з центром в точці О описане навколо трикутника АВС.
Наслідок. Серединні перпендикуляри до сторін трикутника перетинаються в одній точці.
ОК – серединний перпендикуляр до відрізка СВ (СК = КВ, ОК ﬩ СВ).
ОМ – серединний перпендикуляр до відрізка АВ (АК = КВ, ОМ ﬩ АВ).
ОР – серединний перпендикуляр до відрізка АС (АР = РС, ОР ﬩ АС).
Точка О – точка перетину серединних перпендикулярів ОК, ОМ, ОР.
Наслідок. Центром кола, описаного навколо трикутника, є точка перетину серединних перпендикулярів до його сторін.
Точка О – точка перетину серединних перпендикулярів, центр кола, описаного навколо трикутника АВС.
Центром кола, описаного навколо прямокутного трикутника, є середина гіпотенузи, а радіус цього кола дорівнює половині гіпотенузи.
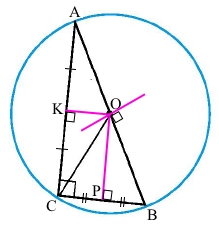
Трикутник АВС – прямокутний трикутник із гіпотенузою АВ (∠С = 90°)
О – центр кола, описаного навколо прямокутного трикутника, тоді
АО = ОВ, r = АВ/2.