Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

^{(умови завдань з підручника подані чорним кольором)}

ВПРАВИ ДЛЯ ПОВТОРЕННЯ РОЗДІЛУ 1

До § 1

Вправа 67

1) точка перетину прямих a і b: М

2) точки належать прямій c: P, L (Р є с, L є c)

3) чи належить точка M прямій PL: не належить ( М ¢ PL)

4) як інакше можна назвати пряму b:  РМ, або МР

 

Вправа 68

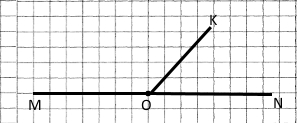
1) Побудуйте промені OK, OM і ON так, щоб промінь OM був доповняльним для променя ON.

Доповняльні промені мають спільний початок і лежать на одній прямій.

 

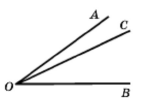
2) Побудуйте промені OA, OB і OC так, щоб серед побудованих променів не було жодної пари доповняльних.

Не лежать на одній прямій зі спільним початком.  

 

Вправа 69

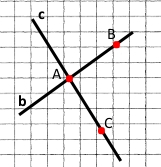
Позначте точки A, B і C так, щоб записи AB і AC озна­чали дві різні прямі.

А – точка перетину двох прямих b і c. 

 

Вправа 70

Одна з двох прямих, що перетинаються, проходить через точку M, яка належить іншій прямій. Що можна сказати про точку M і точку перетину цих прямих?

Оскільки точка М належить одній прямій, а іншій – не належить, тому точка М не є точкою перетину прямих.

 

Вправа 71

Точки A і B належать прямій l. Пряма m відмінна від прямої l і проходить через точку A. Чи може точка B нале­жати прямій m? Відповідь обґрунтуйте.

Якщо точка А належить двом різним прямим l та m, то що означає – прямі перетинаються в точці А. Оскільки прямі різні, тоді вони перетинаються тільки в одній точці, отже, точка В не може належати прямій m.

Відповідь: не належить.  

 

До § 2

Завдання 72

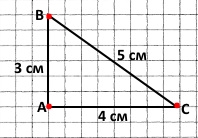
1) Позначте в зошиті точки A, B і C, які не лежать на одній прямій, та знайдіть відстані між кожною парою точок.

АВ = 3 см

ВС = 5 см

АС = 4 см

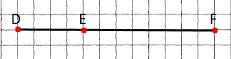
2) Позначте в зошиті точки D, E і F, які лежать на одній прямій, та знайдіть відстані між кожною парою точок.

DF = 6 см

DE = 2 см

EF = 4 см

 

Завдання 73

Накресліть відрізок KL = 6 см 8 мм. Позначте на ньому точку P так, що KP = 43 мм. Знайдіть довжину відрізка LP за допомогою обчислень.

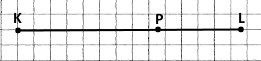
KL = 6 см 8 мм = 68 мм

Якщо точка Р належить відрізку KL, тоді справедлива основна властивість вимірювання відрізків КL = КР + РL. 

LP = PL = KL – KP = 68 мм – 43 мм = 25 мм

 

Завдання 74

Сумою яких двох відрізків є відрізок MN? Розгляньте всі мож­ливі випадки.

MN = MA + AB + BN

MN = MA + (AB + BN) = MA + AN

MN = (MA + AB) + BN = MB + BN

 

Завдання 75

1) Три прямі перетинають відрізок AB, причому жодна з точок перетину прямих і відрізка не збігається з кінцями відрізка. На скільки частин ці точки можуть поділити від­різок?

Якщо три прямі перетинаються в одній точці, тоді буде 2 частини до кінців відрізка.

Якщо дві прямі перетинаються в одній точці, тоді 1 частина між прямими і ще 2 частини до кінців відрізка, разом 3 частини.

Між трьома точками буде 2 частини, і ще 2 частини до кінців відрізків, разом 4.

Відповідь: на 2, 3 або 4 частини. 

 

2) На скільки частин поділиться відрізок, якщо кількість прямих дорівнює n?

Якщо n прямих перетинаються в одній точці, тоді буде 2 частини до кінців відрізка.

Якщо утвориться дві такі точки, тоді буде 1 частина між точками і ще 2 частини до кінців відрізка.

І так до  n + 1 частини.

Відповідь: від 2 до n + 1 частини.

 

Завдання 76

1) Точка C – середина відрізка AB, точка D – середина від­різка AC. Знайдіть AC, CB, AD і DB, якщо AB = 20 см.

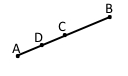
Якщо точка C – середина відрізка AB, тоді АВ = АС + СВ = 2АС;

АС = АВ : 2 = 20 см : 2 = 10 см.

СВ = АС = 10 см.

Якщо точка D – середина від­різка AC, тоді AC = AD + DC = 2AD.

AD = AC : 2 =  10 см : 2 = 5 см.

DС = АD = 5 см.

 

2) Точка C – середина відрізка AB, точка D – середина від­різка AC. Знайдіть AB, AC, AD і DB, якщо BC = 12 дм.

Якщо точка C – середина відрізка AB, тоді АВ = АС + СВ = 2СВ = 2ВС;

АВ = 12 дм • 2 = 24 дм.

АС = ВС = 12 дм.

Якщо точка D – середина від­різка AC, тоді AC = AD + DC = 2AD.

AD = AC : 2 =  12 дм : 2 = 6 дм.

DC = AD = 6 дм

CB = BC = 12 дм

DВ = DC + CB = 6 дм + 12 дм = 18 дм.

 

Завдання 77

Точки M і N належать відрізку CD, CD = 15 см, CM = 12 см, DN = 11 см. Знайдіть довжину відрізка NM.

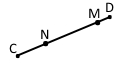
Якщо точка M належить відрізку CD, тоді CD = CM + MD

MD = CD – CM = 15 см – 12 см = 3 см

Якщо точка N належать відрізку CD, тоді СD = CN + ND

CN = CD – DN = 15 см – 11 см = 4 см

Якщо точки M і N належать відрізку CD, тоді CD = CN + NM + MD,

NM = CD – CN – MD = 15 см – 4 см – 3 см = 8 см

 

Завдання 78

Точка P належить відрізку AB. На прямій AB позначте таку точку C, щоб ВС = АР/2. Скільки розв'язків має задача?

Якщо точка P належить відрізку AB, тоді АВ = АР + РВ.

Задача має два розв’язки.

Точка С може лежати справа від точки А.

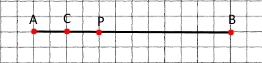
Точка С може лежати зліва від точки А.

 

 

Завдання 79

Точка K належить відрізку CD, довжина якого a см. Знайдіть відстань між серединами відрізків CK і KD.

Якщо точка K належить відрізку CD, тоді CD = CK + KD = а см

Якщо деякі точки А, В будуть серединами відповідних відрізків CK і KD, тоді

СК = СА + AK = 2CA

KD = KB + BD = 2KB

2CA + 2KB = а см

2 • (CA + KB) = a см

CA + KB – відстань між серединами відрізків CK і KD.

CA + KB = a/2 см

 

До § 3

Завдання 80

∠AOB = 40°

∠BOC = 60° – 40° = 20°

∠COD = 120°

∠AOD = 180°

 

Завдання 81

Два учні накреслили кути по 70°. Один з учнів сказав, що в нього кут більший, оскільки сторони його кута мають більшу довжину. Чи правий цей учень?

Учень неправий, оскільки величина кута вимірюється його градусною мірою. Якщо два учні накреслили кути по 70°, тоді їхні кути рівні.

 

Завдання 82

Усі можливі назви кута з вершиною A:

KAМ, або МАК,

КАС, або САК,

ВАС, або АСВ,

ВАМ, або МАВ.

 

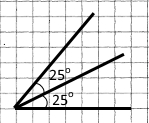
Вправа 83  Бісектриса кута ділить його пополам.

Побудували бісектрису гострого кута 50°.

Побудували бісектрису тупого кута 140°.

 

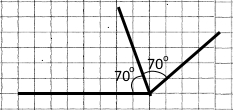
Вправа 84

1) На який кут повертається хвилинна стрілка годинника протягом 15 хв; 7 хв; 23 хв?

Годинник має 60 поділок для хвилинної стрілки, у середині кола годинника градусна міра дорівнює 360, тоді 360 : 60 = 6 (°) – градусна міра між сусідніми поділками.

Щоб знайти градусну міру кута повороту хвилинної стрілки, треба 6° помножити на кількість хвилин.

6° • 15 = 90°

6° • 7 = 42°

6° • 23 = 138°

 

2) На який кут повертається годинна стрілка годинника протягом 1 хв; 6 хв; 40 хв?

6° • 1 = 6°

6° • 6 = 36°

6° • 40 = 240°

 

Вправа 85

OK – бісектриса кута AOB, OL – бісектриса кута KOB. Знай­діть:

1) ∠LOK, якщо ∠AOB = 120°;

Бісектриса ОК ділить кут АОВ пополам, тоді ∠АОВ = ∠АОК + ∠КОВ,

∠КОВ = 1/2 ∠АОВ = 120° : 2 = 60°

Бісектриса OL ділить кут КОВ пополам, тоді ∠КОВ = ∠КОL + ∠LОВ,

∠КОL = ∠LOK = 1/2 ∠KOB = 60° : 2 = 30°

Відповідь: ∠КОL = 30°

 

2) ∠AOB, якщо ∠LOB = 37°.

Бісектриса OL ділить кут КОВ пополам, тоді ∠КОВ = ∠КОL + ∠LОВ

∠КОB = 2 • ∠LOB = 2 • 37° = 74°

Бісектриса ОК ділить кут АОВ пополам, тоді ∠АОВ = ∠АОК + ∠КОВ,

∠AOB = 2 • ∠KOB = 2 • 74° = 148°

Відповідь: ∠AOB = 148°

 

Вправа 86

∠AOB = ∠BOC, ∠COD = ∠DOE.

1) Знайдіть ∠BOD, якщо ∠AOE = 140°;

Якщо промені ОВ, ОС, ОD проходить між сторонами кута АОЕ, тоді справедлива основна властивість вимірювання кутів ∠AOЕ = ∠AOВ + ∠ВOС + ∠COD + ∠DOE,

перегрупуємо доданки ∠AOЕ = ∠AOВ + ∠DOE + ∠BOC + ∠COD.

Оскільки ∠AOB = ∠BOC, ∠COD = ∠DOE, тоді ∠AOЕ = 2 • (∠BOC + ∠COD) = 2 • ∠BOD

∠BOD = ∠AOE : 2 = 140° : 2 = 70°   

Відповідь: ∠BOD = 70°

 

2) ∠AOB, якщо ∠BOD = 73°.

Якщо промені ОВ, ОС, ОD проходить між сторонами кута АОЕ, тоді справедлива основна властивість вимірювання кутів ∠AOЕ = ∠AOВ + ∠ВOС + ∠COD + ∠DOE,

перегрупуємо доданки ∠AOЕ = ∠AOВ + ∠DOE + ∠BOC + ∠COD.

Оскільки ∠AOB = ∠BOC, ∠COD = ∠DOE, тоді ∠AOЕ = 2 • (∠BOC + ∠COD) = 2 • ∠BOD = 2 • 73° = 146°   

Відповідь: ∠AOB = 146°

 

Вправа 87

∠AOB = 168°, промінь OM проходить між його сторонами. ∠AOM : ∠MOB = 3 : 4. Знайдіть ці кути.

Якщо промінь ОМ проходить між сторонами кута АОВ, тоді справедлива основна властивість вимірювання кутів ∠AOB = ∠AOM + ∠MOB.

168 : 7 = 24 (°) – припадає на 1 частину кута AOB.

24 • 3 = 72 (°) – градусна міра кута AOM.

24 • 4 = 96 (°) – градусна міра кута MOB.

Відповідь: ∠АОМ = 72°, ∠МОВ = 96°

Інші завдання дивись тут...