Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 1 Геометричні фігури, точка, пряма, промінь
Завдання 1
1) точки, що належать прямій a: А, В, С.
2) точки, що належать прямій b: Р, В.
3) точку, що належить і прямій і прямій b: В.
4) точки, що належать прямій а, але не належать прямій b: А, С.
5) точки, що не належать ані прямій а, ані прямій b: D, K.
Вправа 2 Позначте в зошиті точки M і N та проведіть через них пряму. Позначте точку K, що належить побудованій прямій, та точку L, яка їй не належить.
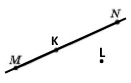
К є MN
L ¢ MN
Вправа 3 Проведіть пряму а. Позначте дві точки, що належать цій прямій, і дві точки, які їй не належать.
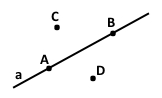
А є а, В є а
С ¢ а, D ¢ а,
Завдання 4 Пряма AB перетинає прямі MN і KL у точках C і D.
1) Усі промені з початком у точці C: СМ, СА, CN, CD, CB.
2) Пари доповняльних променів з початком у точці D: DK і DL, DA і DB, DC і DB.
Завдання 5
1) Усі промені: NM, NP, NK, NF.
2) Пари доповняльних променів: NM і NK.
Завдання 6 Позначте в зошиті точки M, N, F так, щоб через них можна було провести пряму.
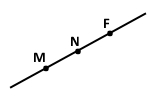
Усі можливі назви цієї прямої: MN, NM, MF, FM, NF, FN.
Завдання 7 Позначте в зошиті точки B, C і D так, щоб записи CD і CB позначали одну й ту саму пряму.
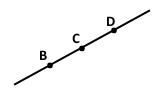
Ще можна назвати цю пряму: DC, DC, BD, DB.
Завдання 8
1) Прямі m і CB перетинаються.
2) Усі точки, які належать прямій m: А, L.
3) Усі точки належать прямій BC: В, С, Q.
4) Точки не належать ані прямій m, ані прямій BC: K, D.
Завдання 9
Позначте точки D, E, F, P, як на малюнку.
1) Через кожні дві точки проведіть пряму.
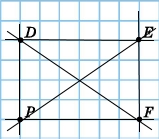
Назви цих прямих: DE, ED, DP, PD, EP, PE, PF, FP, PE, EP, DF, FD.
2) Всього прямих утворилося: шість.
3) На частин прямі розбивають площину: 16.
Завдання 10
Три точки A, B і C не лежать на одній прямій.
1) Через кожні дві точки проведіть пряму.
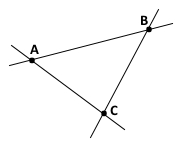
Усі утворені прямі: АВ, ВА, ВС, СВ, АС, СА.
2) Всього прямих утворилося: три.
3) На скільки частин ці прямі розбивають площину: сім.
Завдання 11
Точка A ділить пряму m на два промені.
Точки B і C цієї прямої належать одному променю за умови, що вони лежать по одну сторону точки А.
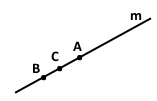
Точки В і С цієї прямої належать різним променям за умови, що вони лежать по різні сторони від точки А.
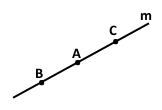
Завдання 12
Парк має форму прямокутника розмірами 800 м і 600 м, по периметру якого є доріжка для бігу, ходьби або велосипедних прогулянок.
1) Семикласник Вадим веде здоровий спосіб життя та щоранку пробігає по доріжці в парку зі швидкістю 14 км/год. Скільки часу витрачає учень на пробіжку?
1) Р = 800 • 2 + 600 • 2 = 1600 + 1200 = 2800 (м) – довжина доріжки (шлях).
2) 14 км/год = 14 км : 1 год = 14000 м : 60 хв = 14000/60 = 140/6 м/хв
2800 м : 140/6 = (2800•6)/140 = 20 • 6 = 120 (хв) = 2 (год)
Відповідь: за 2 год.
2) Батьки Вадима також ведуть здоровий спосіб життя та щовечора прогулюються доріжкою парку, на це вони витрачають 50 хв. З якою швидкістю прогулюються батьки Вадима?
1) 2800 : 50 = 280 : 100 • 2 = 56 (м/хв) – швидкість батьків.
Відповідь: 56 (м/хв)
Завдання 13
Накресліть відрізок MN, позначте на ньому точки А і В.
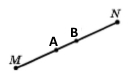
Усі утворені відрізки з кінцями в точках M, N, A і B:
МА, AM, AB, BA, MB, BM, BN, NB, AN, NA, MN, NM.
Завдання 14
Побудуйте відрізки AB і DC так, щоб AB = 5 см, CD = 6 см 2 мм. Порівняйте довжини відрізків.
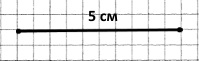
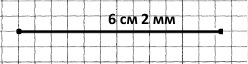
5 см < 6 см 2 мм, тому AB < CD
Завдання 15
На площині проведено три прямі. На першій позначено 2023 точки, на другій – 2024, а на третій – 2025 точок. Яку найменшу загальну кількість точок при цьому може бути позначено?
Якщо три прямі не перетинаються, то сумарно зайво порахованих точок нема.
Якщо три прямі перетинаються в одній точці, то сумарно зайво порахованими будуть 2 точки.
Якщо три прямі перетинаються у двох точках, то сумарно зайво порахованою буде одна точка.
Найменша кількість точок буде, коли три прямі перетинаються у різних точках, тоді сумарно зайво порахованими будуть 3 точки, тому
2023 + 2024 + 2025 – 3 = 6069.