Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 8 Паралельні прямі
Завдання 164
1) пряма а паралельна прямій m: а ǁ m
2) пряма CD паралельна прямій PK: CD ǁ PK
Завдання 165 На яких з малюнків 8.5-8.8 зображено паралельні прямі?
Паралельні прямі не перетинаються.
8.5, 8.8
Завдання 166 Малюнок 8.9.
Паралельні прямі не перетинаються.
Пари паралельних прямих: m ǁ a, b ǁ n
Завдання 167 Дано пряму b і точку K, що їй не належить.
1) За аксіомою паралельності прямих через точку К можна провести тільки одну пряму, яка буде паралельна прямій b.
2) Взагалі можна провести безліч прямих, паралельних прямій b.
Завдання 168 Побудова паралельних прямих
Проведіть пряму l позначте точку A, що їй не належить. За допомогою косинця і лінійки через точку A проведіть пряму, паралельну прямій l.
Через точку А можна провести тільки одну паралельну пряму до прямої l.
Завдання 169 Позначте точку P і проведіть пряму а, що не проходить через цю точку. За допомогою косинця і лінійки через точку P проведіть пряму, паралельну прямій а.
Через точку А можна провести тільки одну паралельну пряму до прямої l.
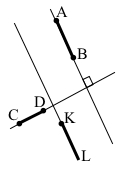
Завдання 170 Побудова перпендикулярних прямих
Накресліть відрізки AB і CD та промінь KL так, щоб відрізок AB був паралельний променю KL і перпендикулярний до відрізка CD.
Перпендикулярні відрізки АВ і CD мають лежати на перпендикулярних прямих.
Промінь KL має лежати на прямій, яка буде паралельна до прямої, якій належить відрізок АВ.
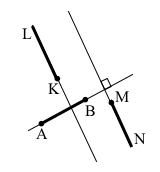
Завдання 171 Накресліть промені MN і KL та відрізок AB так, щоб промінь MN був паралельний променю KL і перпендикулярний до відрізка AB.
Перпендикулярні промінь MN і відрізок АВ мають лежати на перпендикулярних прямих.
Промінь KL має лежати на прямій, паралельній до прямої, якій належить промінь MN.
Завдання 172
1) Накреслили ∠ABC = 120° та позначили точку K, що лежить у внутрішній області цього кута.
Кут ділить площину на дві частини – внутрішню кута (усередині кута) та зовнішню (поза кутом).
2) Через точку K за допомогою косинця і лінійки провели пряму m, паралельну променю BA, та пряму n, паралельну променю BC.
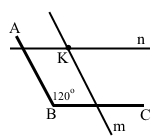
3) Використовуючи транспортир, знайшли кут між прямими.
∠К = ∠АВС = 120°
Знайшли кут між прямими m і n, що перетинаються, 180° – ∠К = 180° – 120° = 60°.
Кутом між прямими не перевищує 90°.
4) Висновок: кут між прямим m і n дорівнює 60°.
Завдання 173
1) Накреслили ∠MNL, який дорівнює 50°, і позначили точку C, що належить внутрішній області цього кута.
Кут ділить площину на дві частини – внутрішню кута (усередині кута) та зовнішню (поза кутом).
2) Через точку C за допомогою косинця і лінійки провели пряму a, паралельну променю NM, і пряму b, паралельну променю NL.
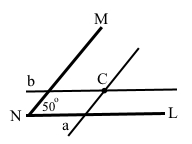
3) Використовуючи транспортир, знайшли кут між прямими.
∠С = ∠АВС = 50°
Оскільки він є меншим із вертикальних кутів із вершиною С, він і буде шуканим кутом між прямими.
Кутом між прямими є менший серед вертикальних кутів.
4) Висновок: кут між прямим m і n дорівнює 50°.
Завдання 174
Прямі a і b перетинаються. Пряма m паралельна прямій a. Доведіть, що прямі m і b перетинаються.
Дано, що прямі а і b перетинаються, прямі m ǁ a.
Доведення.
Нехай прямі a і m паралельні. Оскільки пряма b перетинає пряму а, яка паралельна прямій m, тоді вона перетинає другу паралельну пряму m. Отже, прямі m і b перетинаються.
Завдання 175 Прямі a і b паралельні. Пряма l не перетинає пряму a. Доведіть, що пряма l не перетинає пряму b.
Дано прямі a ǁ b, пряма l не перетинає пряму a.
Доведення (від супротивного).
Нехай пряма l перетинає одну з паралельних прямих b. Тоді вона перетинає другу паралельну пряму а. Це суперечить умові, що пряма l не перетинає пряму а. Отже, пряма l не перетинає пряму b.
Завдання 176 Малюнок 8.11. Прямі KM і KN перетинаються. Через точку M проведено пряму m, паралельну прямій KN, а через точку N проведено пряму n, паралельну прямій KM. Доведіть, що прямі m і n перетинаються.
Дано прямі a ǁ b , с ǁ b, пряма l перетинає пряму a.
Доведення.
Нехай пряма l перетинає одну з паралельних прямих а, тоді вона перетинає другу паралельну пряму b. Оскільки пряма l перетинає одну з паралельних прямих b, тоді вона перетинає другу паралельну їй пряму с. Отже, пряма l перетинає прямі b і c.
Завдання 177 Прямі a і b – паралельні, прямі b і c також паралельні. Пряма l перетинає пряму a. Доведіть, що пряма l перетинає прямі b і c.
Дано прямі a ǁ b , с ǁ b, пряма l перетинає пряму a.
Доведення.
Нехай пряма l перетинає одну з паралельних прямих а, тоді вона перетинає другу паралельну пряму b. Оскільки пряма l перетинає одну з паралельних прямих b, тоді вона перетинає другу паралельну їй пряму с. Отже, пряма l перетинає прямі b і c.
Завдання 178
На прямій m позначили точки A і B та точку C, яка не належить прямій m.
Якщо точка С не належить прямій, тоді AB < AC + BC.
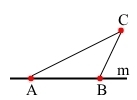
Висновок: якщо точка С не лежить між двома точками А і В прямої, тоді AB < AC + BC.
Завдання 179 Один із вертикальних кутів, що утворилися при перетині двох прямих, становить 25% від іншого. Знайдіть кут між прямими.
При перетині двох прямих утворюються дві пари вертикальних кутів. Оскільки кути нерівні, вони належать різним парам. Вертикальні кути різних пар суміжні, тобто вони утворюють розгорнутий кут, їхня сума дорівнює 180°.
Нехай х (°) – більший кут, тоді 0,25 х (°) – менший кут. Складемо рівняння.
х + 0,25х = 180
1,25х = 180
х = 144 (°) – більший кут.
0,25х = 144 • 0,25 = 36 (°) – кут між прямими (менший кут).
Кут між прямим не повинен перевищувати 90°, тому кутом між прямими буде менший із кутів.
Відповідь: кут між прямими 36°.
Життєва математика
Завдання 180 Дитячий майданчик, що має форму прямокутника 6,5 м завдовжки і 3,5 м завширшки, потрібно вкрити плиткою, що має форму квадрата, довжина сторони якого 50 см. Скільки грошей буде витрачено на це, якщо одна плитка коштує 52 грн, а вартість додаткових матеріалів та укладання становить 35 % від вартості плитки?
Короткий запис
Довжина — 6,5 м
Ширина — 3,5 м
S — ?
1) 6,5 • 3,5 = 22,75 (м2) – площа дитячого майданчика.
Короткий запис
Сторона — 50 см
S — ?
2) 50 см = (50 см : 100) = 0,5 м
0,5 • 0,5 = 0,25 (м2) – площа квадратної плитки.
Короткий запис
1 плитка — 0,25 м2
? плиток — 22,75 м2
3) 22,75 : 0,25 = 91 (пл.) – потрібно плиток.
Короткий запис
Плитки — 91 шт. по 52 грн
Додатково — 35% від плитки
Всього — ?
4) 52 • 91 = 4732 (грн) – вартість плитки.
5) 4732 : 100 • 35 = 1656,2 (грн) – додаткова вартість.
6) 4732 + 1656,2 = 6388, 2 (грн) – грошей буде витрачено.
Відповідь: було витрачено 6388,2 грн.
Завдання 181 Чи можна квадрат, довжина сторони якого дорівнює 2017 клітинок, розрізати на дві рівні фігури так, щоб лінії розрізів проходили по сторонах клітинок?
Площа квадрата буде непарне число, бо 7 • 7 = 49, 9 – остання цифра числа. Непарне число не ділиться на 2, тому квадрат не можна розділити на дві рівні фігури.
Рівні фігури при накладанні суміщаються.