ГДЗ 7 клас геометрія перша та друга ознаки рівності трикутників Істер

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

^{(умови завдань з підручника подані чорним кольором)}

§ 13 Перша та друга ознаки рівності трикутників

Завдання 319

На малюнку 13.1 трикутники рівні між собою за першою ознакою (двома сторонами і кутом між ними).

На малюнку 13.2 трикутники рівні між собою за другою ознакою (стороною і прилеглими кутами).

Завдання 320

На малюнку 13.3 трикутники рівні між собою за першою ознакою (двома сторонами і кутом між ними).

На малюнку 13.4 трикутники рівні між собою за другою ознакою (стороною і прилеглими кутами 30° і 90°).

Завдання 321

На малюнку 13.5 спільний елемент трикутників ABC і CDA – сторона АС.

На малюнку 13.6 спільний елемент трикутників KML і KNP – кут К.

Завдання 322 Малюнок 13.7

Доведіть, що ∆ABC = ∆ADC, якщо BC = CD і ∠ACB = ∠ACD.

Сторона АС – спільна сторона. За умовою BC = CD, ∠ACB = ∠ACD. Отже, за першою ознакою рівності трикутників ∆ABC = ∆ADC.

Завдання 323 Малюнок 13.8

Дано: AB = BC, BK ⊥ AC. Довести: ∆ABK = ∆CBK.

Сторона ВК – спільна сторона. За умовою AB = BC, BK ⊥ AC, тоді ∠АВК = ∠СВК = 90°.

Отже, за першою ознакою рівності трикутників ∆ABK = ∆CBK.

Завдання 324 Малюнок 13.9

Дано: MK = KN, ∠M = ∠N, PL ⊥ MN. Довести: ∆MKP = ∆NKL.

За умовою PL ⊥ MN, тоді ∠MKP = ∠NKL = 90°, сторони MK = KN, кути ∠M = ∠N. Отже, за другою ознакою рівності кутів ∆MKP = ∆NKL.

Завдання 325 Малюнок 13.10

Доведіть, що ∆ABK = ∆DCK, якщо KB = KC і ∠ABK = ∠DCK.

При перетині прямих вертикальні кути ∠АКВ = ∠DKC. За умовою KB = KC і ∠ABK = ∠DCK. Отже, за другою ознакою трикутників ∆ABK = ∆DCK.

Завдання 326 Малюнок 13.11

Доведіть, що ∆ABC = ∆DCB, якщо AB = CD і ∠ABC = ∠BCD.

Сторона СВ – спільна. За умовою AB = CD і ∠ABC = ∠BCD. Отже, за першою ознакою рівності трикутників ∆ABC = ∆DCB.

Завдання 327 Малюнок 13.12

Промінь OC є бісектрисою кута AOB, ∠OCM = ∠OCN. Доведіть, що ∆OMC = ∆ONC.

Сторона ОС спільна. За умовою бісектриса ОС кута АОВ ділить його пополам МОС = NOC, також ∠OCM = ∠OCN. Отже, за другою ознакою трикутників ∆OMC = ∆ONC.

Завдання 328 Малюнок 13.13

Промінь BK є бісектрисою кута ABC, MN ⊥ BK. Доведіть, що MO = ON.

За умовою промінь BK є бісектрисою кута ABC, він ділить кут пополам ∠MBO = ∠NBO.

Пряма NM та промінь BK перетинаються під прямим кутом, ∠BOM = ∠BON = 90°.

Сторона ВО спільна для трикутників BOM і BON. Тоді за другою ознакою трикутників ∆BOM = ∆BON. Отже, MO = ON.

Завдання 329 Малюнок 13.14

Дано: AO = OC, BO = OD. Довести: AB = CD, BC = AD.

Між відрізками BD і AC, що перетинаються, утворюється дві пари вертикальних кутів ∠BOA = ∠DOC і ∠BOС = ∠DOА. За умовою AO = OC, BO = OD.

За першою ознакою трикутників ∆ABO і ∆COD, тоді AB = CD.

За першою ознакою трикутників ∆BOС і ∆DОА, тоді BС = АD.

Отже, AB = CD, BC = AD.

Завдання 330 Малюнок 13.15

Дано: AB = CD, ∠BAC = ∠DCA. Довести: ∆ABC = ∆CDA.

Сторона АС спільна. За умовою сторони AB = CD, також кути ∠BAC = ∠DCA. За першою ознакою рівності трикутників ∆ABC = ∆CDA.

Завдання 331 Малюнок 13.16

Доведіть рівність трикутників MKL і KMP, якщо ∠LMK = ∠PKM і ∠LKM = ∠PMK.

Сторона МК – спільна. За умовою прилеглі кути ∠LMK = ∠PKM і ∠LKM = ∠PMK. Отже, за другою ознакою рівності трикутників ∆MKL = ∆KMP.

Завдання 332 Малюнок 13.17

∆ABC = ∆A₁B₁C₁. На сторонах BC і B₁C₁ позначено відповідно точки L і L₁ такі, що ∠LAC = ∠L₁C₁. Доведіть, що ∆ALC = ∆A₁L₁C₁.

За умовою ∆ABC = ∆A₁B₁C₁, тоді АС = А₁С₁, ∠АСВ = ∠А₁С₁В₁. За другою ознакою рівності трикутників ∆ALC = ∆A₁L₁C₁.

Завдання 333 Малюнок 13.18

∆ABC = ∆A₁B₁C₁. На сторонах AC і A₁C₁ позначено відповідно точки M і M₁ такі, що AM = A₁M₁. Доведіть, що ∆ABM = ∆A₁B₁M₁.

За умовою ∆ABC = ∆A₁B₁C₁, тоді АВ = А₁В₁, ∠ВАС = ∠В₁А₁С₁. За першою ознакою рівності трикутників ∆AВМ = ∆A₁В₁М₁.

Завдання 334

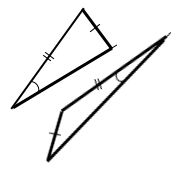
Чи можна стверджувати, що коли дві сторони і кут одного трикутника дорівнюють двом сторонам і куту іншого трикутника, то такі трикутники рівні між собою? Обґрунтуйте, подавши схематичні малюнки.

Якщо мова йде про кут між сторонами, тоді виконуються перша ознака рівності трикутників, отже, можна стверджувати, що трикутники рівні.

Якщо кут не знаходиться між сторонами, тоді не можна застосувати першу ознаку рівності трикутників, отже, не можна стверджувати, що трикутники рівні.

Завдання 335

Чи можна стверджувати, що коли сторона і два кути одного трикутника дорівнюють стороні та двом кутам іншого трикутника, то такі трикутники рівні між собою? Обґрунтуйте, подавши схематичні малюнки.

Якщо мова йде про сторони і прилеглі кути, тоді виконуються друга ознака рівності трикутників, отже, можна стверджувати, що трикутники рівні.

Якщо кути не є прилеглими до сторони, тоді не можна застосувати другу ознаку рівності трикутників, отже, не можна стверджувати, що трикутники рівні.

Завдання 336 Малюнок 13.19

∆ABK = ∆CBL. Доведіть, що ∆ABL = ∆CBK.

За умовою ∆ABK = ∆CBL, тоді АВ = ВС, AK = CL, ∠BAK = ∠BCL.

За властивістю вимірювання відрізків AL = AK + KL, KC = KL + LC, якщо рівні ліві частини рівності, тоді рівні праві частини. Отже, за першою ознакою рівності трикутників ∆ABL = ∆CBK.

Завдання 337 Малюнок 13.19

∆AKC = ∆ALC. Доведіть, що ∆BKC = ∆BLC.

За умовою ∆AKC = ∆ALC, тоді КС = LC, ∠ACK = ∠ACL.

За основною властивістю вимірювання суміжних кутів ACB = ACK + KCB = АСL + LCB,

за умовою ∠ACK = ∠ACL, значить ∠КСВ = ∠LСВ. Сторона СВ – спільна. Отже, за першою ознакою вимірювання кутів ∆BKC = ∆BLC.

Завдання 338

На бісектрисі кута A позначили точку B, а на його сторонах такі точки M і N, що ∠ABM = ∠ABN. Доведіть, що MN ⊥ AB.

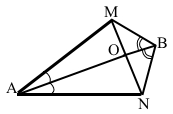
Промінь AB — бісектриса кута А, то ∠MAB = ∠NAB. AB — спільна сторона трикутників ABM і ABN. За умовою ∠ABM = ∠ABN, тоді за другою ознакою рівності трикутників ∆ABM = ∆ABN. Для рівних трикутників AM = AN. AO — спільна сторона трикутників AOM і AON. За умовою ∠MAO = ∠NAO як кути між бісектрисою, тоді за першою ознакою рівності трикутників ∆АОМ = ∆АОN. Для рівних трикутників ∠АОМ = ∠АОN.

При перетині прямих утворюються дві пари суміжних кутів. За основною властивістю вимірювання кутів ∠MON = 180° = ∠AOM + ∠AON = 2∠AOM, звідси кут між прямими ∠AOM = 180° : 2 = 90°. Отже, MN ⊥ AB.

Завдання 339

Одна зі сторін трикутника дорівнює 4 дм, що на 12 см менше від другої сторони й удвічі більше за третю. Знайдіть периметр трикутника.

^{Короткий запис}

^{І сторона — 4 дм}

^{ІІ сторона — на 12 см більша, ніж І}

^{ІІІ сторона — удвічі менша, ніж І}

^{Р — ? дм}

Розв’язання

1) 4 + 12 = 16 (дм) – ІІ сторона.

2) 4 : 2 = 2 (дм) – ІІІ сторона.

3) Р = 4 + 16 + 2 = 32 (дм)

відповідь: периметр трикутника 32 дециметри.

Завдання 340

Сума трьох з восьми кутів, що утворилися при перетині паралельних прямих a і b січною c, дорівнює 270°. Чи перпендикулярні прямі a і c; b і c?

При перетині паралельних прямих a і b січною c утворюється по 4 рівні кути.

У такій сумі три кути можуть бути прямими, бо 270° : 3 = 90° , тоді прямі a ⊥ c; b ⊥ c

У такій сумі три кути не можуть бути гострими.

При перетині прямих утворюються пари суміжних кутів, причому для гострого кута суміжним може бути тільки тупий. У сумі може бути гострий кут і два тупих, наприклад 100° + 100° + 70° = 270°, тоді прямі зі січною не будуть перпендикулярними. Отже, не можна стверджувати, що прямі будуть перпендикулярними.

Відповідь: ні.

Життєва математика

Завдання 341

Підлогу кімнати, що має форму прямокутника зі сторонами 3,5 м і 6 м, потрібно вкрити ламінатом з прямокутних дощечок зі сторонами 7 см і 40 см. Скільки потрібно таких дощечок?

_{Короткий запис}

_{Довжина — 600 см}

_{Ширина — 350 см}

_{S— ? см²}

_{Короткий запис}

_{Довжина — 40 см}

_{Ширина — 7 см}

_{S— ? см²}

6 м = 6 • 1 м = 6 • 100 см = 600 см

3,5 м = 3,5 • 1 м = 3,5 • 100 см = 350 см

1) 600 • 350 = 210 000 (см²) – площа підлоги кімнати.

2) 40 • 7 = 280 (см²) – площа дощечки.