Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
Домашня самостійна робота № 3 (§§ 11-16)
Завдання 1
Дано ∆KLM, у якого KM = 4 см, ML = 7 см, KL = 10 см. Знайдіть його периметр.
Р = КМ + МL + LK = KM + ML + KL = 4 + 7 + 10 = 21 (см)
А 20 см Б 21 см В 22 см Г 23 см
Завдання 2
∆PTK – різносторонній, ∆ABC = ∆PTK. Тоді буде правильною рівність ∠B = ...
Якщо ∆ABC = ∆PTK, тоді рівні відповідні кути: ∠А = ∠Р, ∠В = ∠Т, ∠С = ∠К.
A ∠P Б ∠Т
B ∠K Г жодному з кутів трикутника PTK
Завдання 3
Дано ∆АВС і ∆А1В1С1, де AB = A1B1, ∠A = ∠A1, ∠B = ∠B1.
A ∆АВС = ∆А1В1С1 (за першою ознакою – двома сторонами і кутом між ними)
Б ∆АВС = ∆А1В1С1 (за другою ознакою – стороною і прилеглими кутами)
B ∆АВС = ∆А1В1С1 (за третьою ознакою – трьома сторонами)
Г не можна встановити рівність трикутників АВС і А1В1С1
Завдання 4
Периметр рівнобедреного трикутника дорівнює 17 см, а його основа – 5 см. Знайдіть бічну сторону трикутника.
Короткий запис
Бічні — 2 сторони по ? см
Основа — 5 см
Р — 17 см
Розв’язання
1) 17 – 5 = 12 (см) – сума бічних сторін.
2) 12 : 2 = 6 (см)
А 12 см Б 10 см В 8 см Г 6 см
Завдання 5
Сторони LO = ON, KO = OM, ∠KOL ≠ ∠LOM. Укажіть правильну рівність.
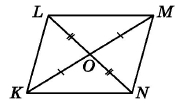
За умовою сторони LO = ON, KO = OM. Вертикальні кути рівні ∠LOK = ∠NOM, ∠LOM = ∠NOK. За першою ознакою рівності трикутників маємо 2 пари рівних: ∆KOL = ∆MON, ∆LOM = ∆NOK.
A ∆KOL = ∆LOM Б ∆KOL = ∆OMN
B ∆KOL = ∆ MON Г ∆KOL = ∆NOM
Завдання 6
AM, BN і CL – медіани трикутника ABC. Яка з них є ще й бісектрисою і висотою трикутника, якщо ∠A = ∠B, а ∠B ≠ ∠C?
За умовою ∠A = ∠B, тоді за ознакою про рівні кути маємо рівнобедрений трикутник із основою АВ. Медіана, проведена з вершини С до основи АВ є бісектрисою і висотою рівнобедреного трикутника. Отже, CL – шукана медіана.
А АМ Б ВN В. CL Г. жодна
Завдання 7
Одна зі сторін трикутника вдвічі менша від другої і на 2 см менша від третьої. Знайдіть найбільшу сторону трикутника, якщо його периметр дорівнює 22 см.
Короткий запис
І сторона — х (см)
ІІ сторона — 2х (см)
ІІІ сторона — х + 2 (см)
Р — 22 см
Нехай х (см) – перша сторона, тоді 2х (см) – друга сторона, х + 2 (см) – третя сторона. Складемо рівняння.
х + 2х + х + 2 = 22
4х + 2 = 22
4х = 22 – 2
4х = 20
х = 20 : 4
х = 5 (см) – перша сторона трикутника.
2х = 2 • 5 = 10 (см) – найбільша сторона трикутника.
А 5 см Б 7 см В 9 см Г 10 см
Завдання 8
Відомо, що ∆KLM = ∆MLK. Знайдіть периметр трикутника KLM, якщо KL = 6 см, KM = 5 см.
За умовою ∆KLM = ∆MLK, тоді ∠K = ∠M, згідно ознаки трикутника з двома рівними кутами маємо рівнобедрений трикутник с основою КМ, тоді Р = 2 • 6 + 5 = 17 (см)
А 17 см Б 16 см В 18 см Г знайти неможливо
Завдання 9
BK – висота трикутника АВС, AB = BC. Укажіть неправильне твердження.
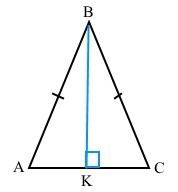
За означенням маємо рівнобедрений трикутник з основою АС.
а) ВК – висота до основи АС, тому ∠ВКА = 90°. Твердження ∠АВС = ∠ВКА = 90° правильне тільки для прямокутного рівнобедреного трикутника АВС.
б) При основі АС кути рівні ∠ВАС = ∠ВСА. Правильне твердження.
в) Оскільки ВК – висота і медіана до основи АС, АК = КС, ∠ВКА = ∠ВКС = 90°, а ВК – спільна сторона, тому за першою ознакою рівності трикутників ∆BAK = ∆ВCK. Правильне твердження.
г) Оскільки ВК – висота з вершини В до основи є бісектрисою, тому ∠ABK = ∠СBK. Правильне твердження.
A ∠АВС = ∠BKA Б ∠ВАС = ∠ВСА
B. ∆BAK = ∆ВCK Г ∠ABK = ∠СBK
Завдання 10
Дано: ∆ABC = ∆BCA, AB = 5 см. Знайти: BC, CA.
За умовою ∆ABC = ∆BCA, тоді відповідні кути А = В, В = С, С = А, звідси А = В = С. З наслідку ознаки рівнобедреного трикутника маємо рівносторонній трикутник. Отже, ВС = СА = 5 см.
A ВС = 6 см, СА = 7 см Б ВС = 4 см, СА = 3 см
B ВС = 4 см, СА = 4 см Г ВС = 5 см, СА = 5 см
Завдання 11
AB – основа рівнобедреного трикутника ABC, CK – його бісектриса. Знайдіть довжину цієї бісектриси, якщо периметр трикутника ABC дорівнює 36 см, а периметр трикутника ACK дорівнює 30 см.
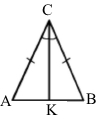
За умовою АВС – рівнобедрений трикутник з основою АВ, тоді СА = СВ.
За умовою СК – бісектриса, тоді СК – медіана до основи АВ, тому АК = КВ, АК + КВ = АВ.
2PАСК = АС + АК + СК + СК + СВ + КВ = (АС + СВ) + (АК + КВ) + 2СК
2PАСК = АС + СВ + АВ + 2СК
2PАСК = PАВС + 2СК
2СК = 2PАСК – PАВС = 2 • 30 – 36 = 24 (см)
СК = 24 : 2 = 12 (см)
2 спосіб
За умовою АВС – рівнобедрений трикутник з основою АВ, тоді СА = СВ.
За умовою СК – бісектриса, тоді СК – медіана до основи АВ, тому АК = КВ, АК + КВ = АВ.
PАВС + 2СК = 2PАСК
СК = (2PАСК – PАВС) : 2 = (2 • 30 – 36) : 2 = 12 (см)
A 6 см Б 8 см
B 10 см Г 12 см
Завдання 12
У трикутнику ABC AB = AC. Точка M така, що BM = MC. Укажіть неправильне твердження.
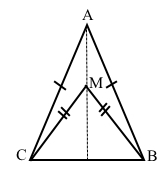
а) Трикутник СМВ – рівнобедрений з основою СВ, кути при основі рівні ∠МВС = ∠МСВ. Твердження правильне.
б) За умовою AB = AC, BM = MC, АМ – спільна сторона трикутників MBA і MCA. Трикутники ∆MBA = ∆MCA за третьою ознакою рівності трикутників, тому ∠МВА = ∠МСА. Твердження неправильне.
A ∠МВС = ∠МСВ Б ∠МВА > ∠МСА
B ∠ВМА = ∠СМА Г ∠ВАМ = ∠САМ
Завдання 13 Периметр трикутника ABC дорівнює 37 см, AB : BC = 2 : 3, AC – AB = 2 см. Установіть відповідність між сторонами трикутника та їхніми довжинами.
Р = 37 см, AB : BC = 2 : 3, AC = АВ + 2
2х (см) – сторона АВ, 3х (см) – сторона ВС, 2х + 2 (см) – сторона АС.
2х + 3х + 2х + 2 = 37
7х + 2 = 37
7х = 37 – 2
7х = 35
х = 35 : 7
х = 5
2х = 2 • 5 = 10 (см) – АВ.
3х = 3 • 5 = 15 (см) – ВС.
2х + 2 = 2 • 5 + 2 = 12 (см) – АС.
1 AB ——> А 10 см
2 BC ——> В 15 см
3 CA ——> Б 12 см
Завдання для перевірки знань до §§ 11-16
Завдання 1 Накресліть ∆MNK. Запишіть назви вершин, сторін та кутів трикутника.
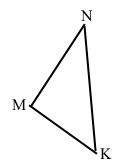
Вершини: М, N, K.
Сторони: MN, NK, MK.
Кути: ∠М, ∠N, ∠K.
Завдання 2 Малюнок 16.14
Трикутник гострокутний АВС,
трикутник прямокутний KMN,
трикутник тупокутний PQR.
Завдання 3 Малюнок 16.15.
Трикутник рівнобедрений ABK
трикутник рівносторонній CDM
трикутник різносторонній FPM
Завдання 4
∆ABC = ∆KMF. Відомо, що AB = 5 см, BC = 4 см, KF = 7 см. Знайдіть невідомі сторони трикутників ABC і KMF.
AB = KM = 5 см, BC = MF = 4 см, AC = KF = 7 см.
Відповідь: KM = 5 см, MF = 4 см, AC = 7 см.
Завдання 5 Малюнок 16.16
MK = KN, ∠LKM = ∠LKN. Доведіть, що ∆MKL = ∆NKL.
За умовою MK = KN, ∠LKM = ∠LKN. KL – спільна сторона трикутників MKL і NKL. Отже, за першою ознакою рівності трикутників ∆MKL = ∆NKL.
Завдання 6 Знайдіть периметр рівнобедреного трикутника з основою 12 см завдовжки, бічна сторона якого на 3 см більша за основу.
Короткий запис
Основа — 12 см
Бічна сторона — на 3 см більша,
Бічна сторона — стільки ж.
Р — ?
Розв’язання
1) 12 + 3 = 15 (см) – бічна сторона.
2) Р = 15 + 15 + 12 = 42 (см) – периметр рівнобедреного трикутника.
Відповідь: Р = 42 см.
Завдання 7 Малюнок 16.17
AC = BD, BC = AD. Доведіть, що ∠BCD = ∠ADC.
За умовою AC = BD, BC = AD. Відрізок CD – спільна сторона трикутників BCD і ADC. За третьою ознакою рівності трикутників ∆BCD = ∆ADC. Отже, відповідні кути рівні ∠BCD = ∠ADC.
Завдання 8
Одна сторона трикутника вдвічі менша від другої і на 3 см менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 23 см.
Короткий запис
І сторона — 2х (см)
ІІ сторона — х (см)
ІІІ сторона — х + 3 (см)
Р — 23 см
Нехай х (см) – друга сторона, тоді 2х (см) – перша сторона, х + 3 (см) – третя сторона. Складемо рівняння.
х + 2х + х + 3 = 23
4х + 3 = 23
4х = 23 – 3
4х = 20
х = 20 : 4
х = 5 (см) – друга сторона.
2х = 2 • 5 = 10 (см) – перша сторона.
х + 3 = 5 + 3 = 8 (см) – третя сторона.
Відповідь: 10 см, 5 см, 8 см.
Завдання 9
У рівнобедреному трикутнику KML з основою KL проведено медіану MP. Знайдіть периметр трикутника KML, якщо MP = 8 дм, а периметр трикутника MKP дорівнює 24 дм.
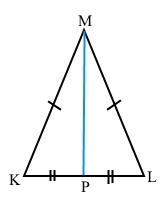
За умовою у рівнобедреному трикутнику МК = LM.
МР – медіана до основи KL, тому KР = РL, KР + РL = KL.
2РМКР = МК + КР + МР + МР + PL + LM = MK + KL + MP + 2MP
2РМКР = PKML + 2MP
PKML = 2PМКР – 2MP = 2 • (PМКР – MP) = 2 • (24 – 8) = 2 • 16 = 32 (дм)
Відповідь: PKML = 32 дм.
Додаткові вправи
Завдання 10
∆ANB = ∆AMB. Доведіть, що NC = MC.
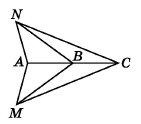
За умовою ∆ANB = ∆AMB, тоді AN = AM, ∠NAB = ∠MAB. AC – спільна сторона трикутників CNA і CMA, за першою ознакою рівності трикутників ∆CNA = ∆CMA. Отже, NC = MC.
Завдання 11
Відомо, що ∆MKL = ∆KLM. Знайдіть периметр трикутника MKL, якщо він на 10 см більший за сторону MK.
За умовою ∆MKL = ∆KLM, тоді МК = KL, KL = LM, ML = KM, маємо рівносторонній трикутник (MK = KL = LM).
Нехай х (см) – сторона МК, тоді P – х = 10, для рівностороннього трикутника Р = 3х, тоді 3х – х = 10
2х = 10
х = 10 : 2
х = 5 (см) – довжина сторони трикутника.
Р = 3х = 3 • 5 = 15 (см)
Відповідь: РMKL = 15 см.