Висотою трикутника називають перпендикуляр, проведений з вершини трикутника до прямої, що містить його протилежну сторону.
Основа перпендикуляра є основою висоти трикутника.
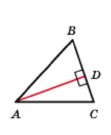
АD – висота трикутника з вершини А, ∠BDA = ∠CDA.
Точка D – основа висоти трикутника з вершини А.
Будь-який трикутник має три висоти.
У будь-якому трикутнику три висоти або їхні продовження перетинаються в одній точці.
Ортоцентр трикутника – точка перетину висот трикутника.
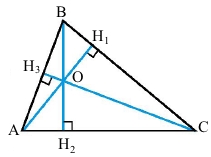
АН1 – висота трикутника з вершини А, ∠BН1A = ∠CН1A = 90°.
ВН2 – висота трикутника з вершини В, ∠АН2В = ∠CН2В = 90°.
СН3 – висота трикутника з вершини С, ∠BН3С = ∠АН3С = 90°.
О – ортоцентр трикутника АВС.
◊ Наслідок із властивості бісектриси рівнобедреного трикутника.
Висота рівнобедреного трикутника, проведена до основи, є медіаною і бісектрисою.
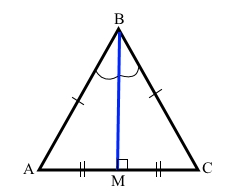
∆АВС – рівнобедрений трикутник, тоді
ВМ – висота трикутника до основи, ∠АМВ = ∠СМВ = 90°;
ВМ – медіана трикутника до основи, АМ = МС;
ВМ – бісектриса трикутника до основи, ∠АВМ = ∠СВМ, ∠АВС = 2∠АВМ.