Медіана трикутника – це відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
Точку медіани, яка є серединою протилежної сторони, називають основою медіани.
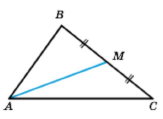
АМ – медіана з вершини А, тоді М – основа медіани АМ, МВ = МС.
Будь-який трикутник має три медіани.
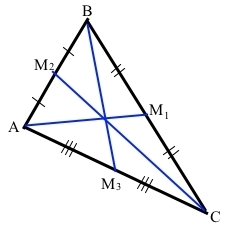
АМ1 – медіана з вершини А, М1В = М1С, М1 – основа медіани АМ1.
СМ2 – медіана з вершини С, М2А = М2В, М2 – основа медіани СМ2.
ВМ3 – медіана з вершини В, М3А = М3С, М3 – основа медіани ВМ3.
У будь-якому трикутнику медіани перетинаються в одній точці.
Центроїд трикутника – це точка перетину трьох медіан трикутника.
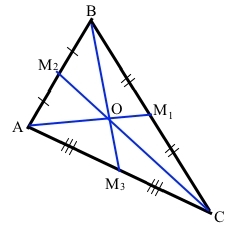
Точка О – центроїд трикутника.
АМ1, СМ2, ВМ3 – медіани.
АМ1 – медіана з вершини А, М1В = М1С, М1 – основа медіани АМ1.
СМ2 – медіана з вершини С, М2А = М2В, М2 – основа медіани СМ2.
ВМ3 – медіана з вершини В, М3А = М3С, М3 – основа медіани ВМ3.
◊ Властивість медіани. У будь-якому трикутнику медіани перетинаються в одній точці (центроїді) і діляться цією точкою у відношенні 2 : 1, починаючи від вершини.
◊ Наслідок із властивості бісектриси рівнобедреного трикутника.
Медіана рівнобедреного трикутника, проведена до основи, є висотою і бісектрисою.
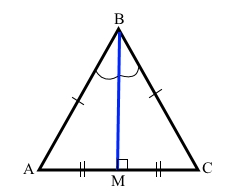
∆АВС – рівнобедрений трикутник, тоді
ВМ – медіана трикутника до основи, АМ = МС;
ВМ – висота трикутника до основи, ∠АМВ = ∠СМВ = 90°;
ВМ – бісектриса трикутника до основи, ∠АВМ = ∠СВМ, ∠АВС = 2∠АВМ.