© Барна Р., 2020
Серія "Вчимось разом" до підручника "Математика 3 клас Заїка А., Тарнавська С."
Завдання 72 Склали вирази
Якщо а = 20, тоді 340 – а = 340 – 20 = 320
Якщо а = 100, тоді 340 – а = 340 – 100 = 240
Якщо а = 120, тоді 340 – а = 340 – 120 = 220
Якщо а = 90, тоді 340 – а = 340 – 90 = 340 – 100 + 10 = 250
Якщо а = 190, тоді 340 – а = 340 – 190 = 340 – 200 + 10 = 150
Якщо а = 0, тоді 340 – а = 340 – 0 = 340
Якщо а = 340, тоді 340 – а = 340 – 340 = 0
Завдання 73
Квадрат — прямокутник, у якого всі сторони рівні.
Квадрат має чотири кути. Кути квадрата прямокутні.
Номери квадратів на рисунку: 2, 5
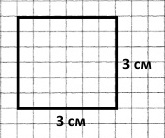
Побудуй квадрат зі стороною 3 см. Обчисли суму довжин усіх сторін цього квадрата.
|
1 спосіб Р = 3 • 4 = 12 (см) – сума довжин усіх сторін квадрата. |
2 спосіб Р = 3 + 3 + 3 + 3 = 12 (см) – сума довжин усіх сторін квадрата. |
Завдання 74
РАВОР = 16 • 4 = (10 + 6) • 4 = 64 (см) – периметр квадрата АВОР.
16 + 16 = 32 (см) – довжина сторони прямокутника ВС або AD.
РABCD = (16 + 32) • 2 = 48 • 2 = 96 (см) – периметр прямокутника ABCD.
Порівняй попарно периметри трьох фігур, що є на рисунку
РАВОР = РРОCD РАВОР < РАВCD РРОCD < РАВCD
Завдання 75 Складена задача
Для прикрашання шкільної новорічної ялинки купили 72 блакитні кульки у 8 однакових упаковках. Упаковок із жовтими кульками купили стільки само, але в кожній упаковці було на 2 кульки менше. Скільки жовтих кульок купили для ялинки?
|
|
Кількість кульок в 1 упаковці |
Кількість упаковок |
Загальна кількість кульок |
|
Блакитні |
? |
8 |
72 кульки |
|
Жовті |
?, на 2 кульки менше |
8 |
? |
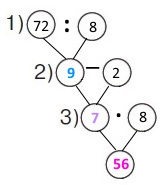
Вираз (72 : 8 – 2) • 8
План розв’язання
1) Скільки блакитних кульок в 1 упаковці?
2) Скільки жовтих кульок в 1 упаковці?
3) Скільки жовтих кульок купили для ялинки?
Розв’язання
1) 72 : 8 = 9 (к.) – блакитних кульок в упаковці.
2) 9 – 2 = 7 (к.) – жовтих кульок в упаковці.
3) 7 • 8 = 56 (к.) – жовтих кульок купили.
Відповідь: купили 56 жовтих кульок.
Завдання 76 Із дроту завдовжки 63 см зробили модель трикутника, що має рівні сторони, і квадрат. Сторона квадрата дорівнює стороні трикутника. Обчисли периметри трикутника й квадрата.
Розв’язання
3 + 4 = 7 (ст.) – сторін у трикутника і квадрата разом.
63 : 7 = 9 (см) – довжина одної сторони трикутника (квадрата).
Р = 9 • 3 = 27 (см) – периметр рівностороннього трикутника зі стороною 9 см.
Р = 9 • 4 = 36 (см) – периметр квадрата зі стороною 9 см.
Завдання 77 Складена задача
Маса трьох однакових динь 9 кг. Якою буде маса 6 кавунів, якщо кожен з них у 2 рази важчий (більше) за диню?
|
|
Маса 1 плода (кг) |
Кількість плодів |
Загальна маса (кг) |
|
Диня |
? |
3 |
9 |
|
Кавун |
?, у 2 рази більша |
6 |
? |
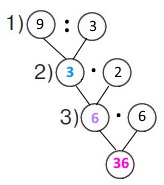
Вираз 9 : 3 • 2 • 6
План розв’язування
1) Яка маса дині?
2) Яка маса кавуна?
3) Якою буде маса шести кавунів?
Розв’язання
1) 9 : 3 = 3 (кг) – маса дині.
2) 3 • 2 = 6 (кг) – маса кавуна.
3) 6 • 6 = 36 (кг) – маса шести кавунів.
Відповідь: маса шести кавунів буде 36 кілограмів.
Завдання 78
|
130 + 80 < 130 + 90 (де більший доданок, там більша сума) 270 – 120 > 270 – 150 (де менший від’ємник, там більша сума) |
380 + 170 < 800 – 200 (520 < 600) 8 • 9 + 9 • 8 = 9 • 9 + 9 • 7 (9 • 9 + 9 • 7 = 9 • 8 + 9 + 9 • 7 = 9 • 8 + 9 • 8) |
Завдання 79, 80 На лівій шальці 3 дині в кошику, а на правій – кавун. Шальки зрівноважені. Яка маса однієї дині, якщо кавун важить 11 кг, а кошик — 2 кг? Маса динь однакова.
Розв’язання
1) 11 – 2 = 9 (кг) – маса трьох динь.
2) 9 : 3 = 3 (кг) – маса дині.
Відповідь: маса дині 3 кілограми.
Завдання 81 Округлення чисел
Замінили числа 22, 180, 205 найближчими до них розрядними, обчислили різницю між поданим числом і розрядним:
22 ≈ 20, 22 – 20 = 2 180 ≈ 200, 200 – 180 = 20 205 ≈ 200, 205 – 200 = 5
Завдання 82 Додавання чисел способом округлення
380 + 150 = (400 – 20) + 150 = (400 + 150) – 20 = 550 – 20 = 530
240 + 470 = 240 + (500 – 30) = (240 + 500) – 30 = 740 – 30 = 710
Завдання 83 Віднімання чисел способом округлення
520 – 290 = 520 – (300 – 10) = 520 – 300 + 10 = (520 – 300) + 10 = 220 + 10 = 230
670 – 180 = 670 – (200 – 20) = 670 – 200 + 20 = (670 – 200) + 20 = 470 + 20 = 490
Завдання 84, 85
Якщо один доданок збільшити на кілька одиниць, щоб число стало круглим, то для того, щоб сума не змінилася, інший доданок слід зменшити на таке саме число.
470 + 180 = (470 + 30) + (180 – 30) = 500 + 150 = 650
530 + 190 = (530 – 10) + (190 + 10) = 520 + 200 = 720
Якщо від’ємник збільшити на кілька одиниць, щоб він став круглим, то для того, щоб різниця не змінилася, зменшуване також слід збільшити на таке саме число.
340 – 280 = (340 + 20) – (280 + 20) = 360 – 300 = 60
720 – 490 = (720 + 10) – (490 + 10) = 730 – 500 = 230
Завдання 86 Складена задача на знаходження суми добутків
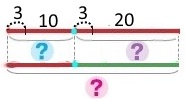
На обіді учні двох класів, в одному з яких 10 учнів, а в іншому — 20, з'їли по 3 сливи кожен. Скільки слив з'їли учні двох класів?
|
1 спосіб Короткий запис Один клас — ? сл., 10 учнів по 3 сливи Інший клас — ? сл., 20 учнів по 3 сливи Всього — ? Схема
Вираз 3 • 10 + 3 • 20 План розв’язування 1) Скільки слив з'їли учні одного класу? 2) Скільки слив з'їли учні іншого класу? 3) Скільки слив з'їли учні двох класів? Розв’язання 1) 3 • 10 = 30 (сл.) – слив з'їли учні одного класу. 2) 3 • 20 = 60 (сл.) – слив з'їли учні іншого класу. 3) 30 + 60 = 90 (сл.) – слив з'їли учні двох класів. |
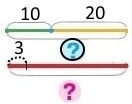
2 спосіб Короткий запис Два класи — ? сл., ? (10 учнів і 20 учнів) по 3 сливи Схема
Вираз 3 • (10 + 20) План розв’язування 1) Скільки всього учнів? 2) Скільки слив з'їли учні двох класів? Розв’язання 1) 10 + 20 = 30 (уч.) – всього учнів. 2) 3 • 30 = 90 (сл.) – слив з'їли учні двох класів. |
Відповідь: учні двох класів з'їли 90 слив.
Завдання 87
У дівчинки 4 купюри по 100 грн і ще 50 грн. У хлопчика 2 купюри по 200 грн і ще 20 гр. У кого більше грошей? На скільки?
1) 100 • 4 + 50 = 100 + 100 + 100 + 100 + 50 = 450 (грн) – гривень у дівчинки.
2) 200 • 2 + 20 = 200 + 200 + 20 = 420 (грн) – гривень у хлопчика.
3) 450 > 420 у дівчинки більше гривень, ніж у хлопчика
450 – 420 = 30 (грн) – на стільки гривень більше у дівчинки, ніж у хлопчика.
Завдання 88 Складена задача на множення
Тонкий зошит коштує 4 грн, а товстий на 8 грн дорожчий за нього. Скільки коштує 2 товсті зошити?
|
Товар |
Ціна (грн) |
Кількість (шт.) |
Вартість (грн) |
|
Тонкий зошит |
4 грн |
|
|
|
Товсті зошити |
?, на 8 грн більше |
2 |
? |
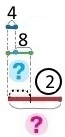
Вираз (4 + 8) • 2

|
Короткий запис №1 Тонкий зошит — 4 грн Товстий зошит — ?, на 8 грн більше |
Короткий запис №3 Вартість — ? грн, 2 товсті зошити по 12 грн |
План розв’язування
1) Скільки гривень коштує товстий зошит?
2) Скільки коштують два товстих зошити?
Розв’язання
1) 4 + 8 = 12 (грн) – гривень коштує товстий зошит.
2) 12 • 2 = 12 + 12 = 24 (грн) – коштують два товстих зошити.
Відповідь: за два товстих зошити треба заплатити 24 гривні.
Завдання 89
На спортивних змаганнях представники трьох команд вишикувалися в ряди, по чотири учасники в кожному. У першій команді було 20 учасників, у другій — на 4 більше, а в третій — на 8 більше, ніж у першій. Скільки рядів спортсменів вишикувалося?
1 спосіб
Ряди І команди — ? р., 20 спортсменів уміщають по 4 спортсмени
ІІ команда — ?, на 20 спортсменів і ще 4 спортсмени
Ряди ІІ команди — ? р., 24 спортсмени уміщають по 4 спортсмени
ІІІ команда — ?, на 20 спортсменів і ще 8 спортсменів
Ряди ІІІ команди — ? р., 28 спортсменів уміщають по 4 спортсмени
Ряди ІІІ команди — ? р., 28 спортсменів уміщають по 4 спортсмени
Вираз 20 : 4 + (20 + 4) : 4 + (20 + 8) : 4
План розв'язування
1) Скільки рядів спортсменів у І команді?
2) Скільки спортсменів у другій команді?
3) Скільки рядів спортсменів у ІІ команді?
4) Скільки спортсменів у третій команді?
5) Скільки рядів спортсменів у ІІІ команді?
6) Скільки рядів спортсменів вишикувалося?
Розв’язання
1) 20 : 4 = 5 (р.) – рядів спортсменів у І команді.
2) 20 + 4 = 24 (сп.) – спортсменів у другій команді.
3) 24 : 4 = 6 (р.) – рядів спортсменів у ІІ команді.
4) 20 + 8 = 28 (сп.) – спортсменів у третій команді.
5) 28 : 4 = 7 (р.) – рядів спортсменів у ІІІ команді.
6) 5 + 6 + 7 = 18 (р.) – рядів спортсменів вишикувалося.
2 спосіб
Короткий запис
І команда — 20 спортсменів
ІІ команда — ?, на 4 спортсмени більше, ніж у І
ІІІ команда — ?, на 8 спортсменів більше, ніж у І
Всього — ?
Ряди — ? р., 72 спортсмени уміщають по 4 спортсмени
Вираз (20 + (20 + 4) + (20 + 8)) : 4
План розв’язування
1) Скільки спортсменів у другій команді?
2) Скільки спортсменів у третій команді?
3) Скільки всього спортсменів?
4) Скільки рядів спортсменів вишикувалося?
Розв’язання
1) 20 + 4 = 24 (сп.) – спортсменів у другій команді.
2) 20 + 8 = 28 (сп.) – спортсменів у третій команді.
3) 20 + 24 + 28 = 72 (сп.) – всього спортсменів.
4) 72 : 4 = (40 + 32) : 4 = 18 (сп.) – рядів спортсменів вишикувалося.
Відповідь: вишикувалося 18 спортсменів.
Завдання 90 Практична робота.
Виготовлення фоторамки з картону…
Завдання 91
а) 20, 40, 60, 80, 100, 120, 140, 160 (наступне число на 20 більше, ніж попереднє)
б) 300, 270, 240, 210, 180, 150, 120, 90 (наступне число на 30 менше, ніж попереднє)
в) 1000, 850, 700, 550, 400, 250, 100 (наступне число на 150 менше, ніж попереднє)
г) 10, 25, 40, 55, 70, 85, 100, 115 (наступне число на 15 більше, ніж попереднє)
Завдання 92
|
430 + 150 = 580 430 + 170 = 500 + 100 = 600 430 + 270 = 600 + 100 = 700 |
430 + 370 = 700 + 100 = 800 430 + 380 = 700 + 110 = 810 430 + 390 = 700 + 120 = 820 |
430 – 350 = 430 – 330 – 20 = 100 – 20 = 80 430 – 250 = 430 – 230 – 20 = 200 – 20 = 180 430 – 150 = 430 – 130 – 20 = 300 – 20 = 280 |
Завдання 93 Проста задача на зменшення на деяке число
Дорослий зубр важить 810 кг, а самка зубра легша (менше кілограмів) від нього на 80 кг. Яка маса самки?
Короткий запис
Зубр — 810 кг
Самка — ?, на 80 кг менше
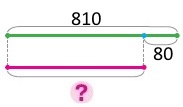
Розв’язання
810 – 80 = 810 – 100 + 20 = 730 (кг)
Відповідь: маса самки 730 кілограмів.
Завдання 94 Виміряли і записали довжини сторін трикутника АВС.
АВ = 3 см, ВС = 4 см
ВС = 5 см
Такий трикутник називають різностороннім. Чому? У нього довжини сторін різні.
Кут АВС прямий.