Інші завдання дивись тут...
§ 7 Завдання 58
Обчисліть ланцюжок виразів і дізнаєтеся довжину (у сантиметрах) гігантської сейшельської черепахи.
319 – 204 + 115 – 210 – 20 + 120 = 120 (см)
Довжина склáдної карликової черепахи становить 12 см. На скільки сантиметрів довжина гігантської черепахи більша за довжину карликової черепахи?
120 – 12 = 108 (см)
Відповідь: на 108 см довжина гіганської черепахи більша.
Завдання 59
Запиши всі можливі трицифрові числа, використовуючи цифри 4, 3 і 8. Знайди суму та різницю найбільшого й найменшого із цих чисел.
348 (найменше число), 384, 438, 484, 834, 843 (найбільше число)
843 + 348 = 1191
843 – 348 = 495
Завдання 60 Рівняння. Обчислення виконай письмово.
|
593 + х = 904 – 135
593 + х = 769
х = 769 – 593
х = 176
|
_ 904
135
469
|
_769
593
176
|
(671 – 292) – х = 213
379 – х = 213
х = 379 – 213
х = 166
|
_671
292
379
|
_ 379
213
166
|
Завдання 61 Добери значення змінних, за яких рівності й нерівності будуть істинними.
453 + 6 = 460 – а, при а = 1
170 + b < 180 + 2, при b = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
756 – 9 > 745 + с, при b = 0, 1.
Завдання 62
Сума трьох чисел дорівнює 1000. Перше число 372, друге — на 129 більше. Знайди третє число.
Короткий запис
Сума — 1000
I — 372
II — ?, на 129 більше
III — ?
Розв’язання
1) 372 + 129 = 501 – II число
2) 372 + 501 = 873 – I і II числа разом
3) 1000 – 873 = 127 – III число
Відповідь: третє число 127.
Завдання 63
Знайди
периметр прямокутника, ширина якого дорівнює 2 см, що на 5 см менше за його довжину. Побудуй
цей прямокутник.
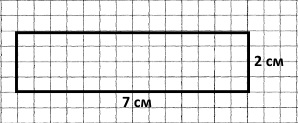
Короткий запис
Ширина — 2 см, це на 5 см менше за довжину
Довжина — ?
Периметр — ?
Розв’язання
1) 2 + 5 = 7 (см) – довжина прямокутника
2) (2 + 7) • 2 = 9 • 2 = 18 (см) – периметр прямокутника
Завдання 64. Брат удвічі старший за сестру, а сестра на 6 років молодша від брата. Скільки років братові й скільки сестрі?
Розв’язання
1-й спосіб
1) 2 – 1 = 1 (ч.) – на стільки частин сестра молодша
2) 6 • 1 = 6 (р.) – років сестрі
3) 6 • 2 = 12 (р.) – років братові
2-й спосіб
Нехай сестрі х років, тобі братові буде 2 • х років. Розв'язуємо рівняння:
2х – х = 6
х = 6 (р.) – років сестрі
2х = 2 • 6 = 12 (р.) – років братові
Відповідь: братові 12 років, сестрі 6 років.
Завдання 65 Рівняння. Обчислення виконай письмово.
|
у – (179 + 237) = 236
у – 416 = 236
у = 236 + 416
у = 652
|
+179
237
416
|
+236
416
652
|
х + 418 = 814 – 325
х + 418 = 489
х = 489 – 418
х = 71
|
_814
325
489
|
_ 489
418
71
|
Завдання 66
Євген, Василина й Катерина утворили групу у вайбері. Євген відправив за рік 236 повідомлень, Василина — на 45 повідомлень менше, ніж Євген, а Катерина — стільки, скільки Євген і Василина разом. Скільки повідомлень відправила Катерина?
Короткий запис
Євген — 236 п.
Василина — ?, на 45 п. менше
Катерина — ?, разом Євген і Василина
Розв’язання
1) 236 – 45 = 191 (п.) – відправила Василина
2) 236 + 191 = 427 (п.)
Відповідь: Катерина відправила 427 повідомлень.
§ 8 Завдання 67 Математичний диктант
Запишіть добутком суму трьох доданків, кожний з яких дорівнює 2.
2 + 2 + 2 = 2 • 3
Запишіть добутком суму чотирьох доданків, кожний з яких дорівнює 4.
4 + 4 + 4 + 4 = 4 • 4
Найбільше одноцифрове число помножте на 5.
9 • 5 = 45
Знайдіть добуток, якщо перший множник — 6, а другий — 8.
6 • 8 = 48
Частку чисел 27 і 9 збільште на 38.
27 : 9 + 38 = 41
Завдання 68
Обчисли значення виразів. До кожного виразу на множення склади по два вирази на ділення.
|
6 • 8 = 48
48 : 6 = 8
48 : 8 = 6
|
7 • 10 = 70
70 : 7 = 10
70 : 10 = 7
|
11 • 9 = 99
99 : 11 = 9
99 : 9 = 11
|
Завдання 69
Добери цифри й числа так, щоб рівності стали істинними.
|
4 • 9 = 36
5 • 6 = 30
7 • 7 = 49
|
2 • 9 = 18
9 • 9 = 81
6 • 6 = 36
|
27 : 9 = 3
48 : 6 = 8
72 : 8 = 9
|
50 : 5 = 10
45 : 9 = 5
64 : 8 = 8
|
Завдання 70 Порядок дій
80 • 1 – 42 : 1 = 80 – 42 = 38
0 • 46 – 0 : 74 = 0
1 • 127 + 93 • 0 = 127 + 0 = 127
415 • 0 + 91 : 91 = 0 + 1 = 1
600 : 100 + 4 • 100 = 6 + 400 = 406
67 • 10 – 670 : 10 = 670 – 87 = 603
Завдання 71
У трьох ящиках було по 8 кг моркви. Скільки всього кілограмів моркви було в трьох ящиках?
Короткий запис
1 ящ. — 8 кг
3 ящ. — ?
Розв’язання
8 • 3 = 24 (кг)
Відповідь: у трьох ящиках було 24 кілограми моркви.
Обернена задача. У трьох однакових ящиках було 24 кг моркви. Скільки кілограмів моркви було в одному такому ящику?
Короткий запис
3 ящ. — 24 кг
1 ящ. — ?
Розв’язання
24 : 3 = 8 (кг)
Відповідь: в одному такому ящику було 8 кілограмів моркви.
Завдання 72
За 3 дні роботи маляр витратив 30 банок
фарби. Скільки банок фарби потрібно малярові на 5 днів роботи, якщо його продуктивність праці не зміниться?
Короткий запис
3 дн. — 30 б.
5 дн. — ?
Розв’язання
1) 30 : 3 = 10 (б.) – банок фарби потрібно на 1 день
2) 10 • 5 = 50 (б.)
Відповідь: малярові потрібно 50 банок фарби на 5 днів роботи.
Обернена задача. За 3 дні роботи маляр витратив 30 банок фарби. На скільки днів роботи потрібно малярові 50 таких банок фарби, якщо його продуктивність праці не зміниться?
Короткий запис
3 дн. — 30 б.
? дн. — 50 б.
Розв’язання
1) 30 : 3 = 10 (б.) – банок фарби потрібно на 1 день
2) 50 : 10 = 5 (дн.)
Відповідь: на 5 днів роботи малярові потрібно 50 таких банок фарби.
Завдання 73
У класі 32 учні. 18 учнів займаються в спортивних секціях, 10 — бальними танцями, 6 — відвідують обидві секції. Скільки учнів класу не займаються в жодній із цих секцій?
Розв’язання
1) 18 – 6 = 12 (уч.) – займаються тільки спортом
2) 10 – 6 = 4 (уч.) – займаються тільки танцями
3) 12 + 4 + 6 = 22 (уч.) – займаються в секціях
4) 32 – 22 = 10 (уч.)
Відповідь: не займаються в жодній із цих секцій 10 учнів.
Завдання 74 Обчисли значення виразів.
9 • 8 + 28 : 4 = 72 + 7 = 79
8 • 7 – 7 • 8 = 56 – 56 = 0
50 : 10 + 36 : 9 = 5 + 4 = 9
8 • 100 – 8 • 5 = 800 – 40 = 760
9 • 9 – 43 = 81 – 43 = 38
7 • 8 + 160 = 56 + 160 = 216
Завдання 75
За 3 год роботи оператор комп’ютерного набору надрукував 27 сторінок. Скільки сторінок надрукує оператор за 5 год такої роботи?
Короткий запис
3 год — 27 с.
5 год — ?
Розв’язання
1) 27 : 3 = 9 (с.) – сторінок надрукує на 1 год роботи
2) 9 • 5 = 45 (с.)
Відповідь: оператор надрукує 45 сторінок за 5 год такої роботи.
Обернена задача. За 3 год роботи оператор комп’ютерного набору надрукував 27 сторінок. За скільки годин такої роботи оператор надрукує 45 сторінок?
Короткий запис
3 год — 27 с.
? год — 45 c.
Розв’язання
1) 27 : 3 = 9 (с.) – сторінок набере на 1 год роботи
2) 45 : 9 = 5 (год)
Відповідь: за 5 годин такої роботи оператор надрукує 45 сторінок.
§ 9 Завдання 76
|
4 • 5 = 20
9 • 5 = 45
10 • 5 = 50
12 • 50 = 600
15 • 5 = 75
60 • 5 = 300
|
15 : 5 = 3
40 : 5 = 8
55 : 5 = 11
80 : 5 = 16
100 : 5 = 20
250 : 5 = 50
|
Завдання 77 Множення і ділення
30 • 3 = 3 дес. • 3 = 9 дес. = 90
120 : 4 = 12 дес. : 4 = 3 дес. = 30
200 • 4 = 2 сот. • 4 = 8 сот. = 800
600 : 2 = 6 сот. : 2 = 3 сот. = 300
Завдання 78 Обчисли значення виразів.
20 • 4 : 2 = 80 : 2 = 40
90 : 3 • 5 = 30 • 5 = 150
300 • 3 : 9 = 900 : 9 = 100
|
80 : 4 • 6 = 20 • 6 = 120
40 • 4 : 8 = 160 : 8 = 20
1000 : 5 • 3 = 200 • 3 = 600
|
Завдання 79 Рівняння
5 • у = 200
у = 200 : 5
у = 40
|
270 : х = 9
х = 270 : 9
х = 30
|
z • 4 = 360
z = 360 : 4
z = 90
|
х : 7 = 140
х = 140 • 7
х = 980
|
Завдання 80
Алла сплела 2 браслети зі 180 бісеринок, порівну на кожний браслет. Скільки бісеринок витратила Алла на кожний браслет? Склади рівняння та розв’яжи задачу.
Короткий запис
2 бр. — 180 б.
1 бр. — х б.
Розв’язання
Нехай х бісеринок сплела на 1 браслет, тоді
х • 2 = 180
х = 180 : 2
х = 90
Відповідь: Алла витратила на кожний браслет 90 бісеринок.
Завдання 81
За добу бамбук виростає на 60 см. На скільки сантиметрів виросте бамбук за 4 доби?
Короткий запис
1 доба — 60 см
4 доби — ?
Розв’язання
60 • 4 = 240 (см)
Відповідь: на 240 см виросте дуб за 4 доби.
Скільки це метрів і сантиметрів?
240 см = 200 см + 40 см = 2 м + 40 см = 2 м 40 см
Завдання 82
У місті запланували посадити 480 дерев. За 2 дні роботи працівники «Зеленбуду» посадили четверту частину всіх дерев. За скільки днів вони посадять усі дерева, якщо продуктивність їхньої праці не зміниться?
Короткий запис
Усього — 480 д.
2 дн. — ?, 1/4 усіх дерев
? дн. — 480 д.
Розв’язання
1) 480 : 4 = 120 (д.) – посадили за два дні
2) 120 : 2 = 60 (д.) – посадили за один день
3) 480 : 60 = 8 (дн.)
Відповідь: усі дерева посадять за 8 днів.
Завдання 83 Рівняння
7 • z = 350
z = 350 : 7
z = 50
|
800 : х = 2
х = 800 : 2
х = 400
|
y • 3 = 180
y = 180 : 3
y = 60
|
х : 6 = 120
х = 120 • 6
х = 720
|
Завдання 84
Віктор склав 4 фігури зі 160 деталей «Лего», витративши на кожну фігуру однакову кількість деталей. Скільки деталей використав Віктор на кожну фігуру? Склади рівняння та розв’яжи задачу.
Короткий запис
4 ф. — 160 д.
1 ф. — х д.
Розв’язання
Нехай х деталей витратив на 1 фігуру, тоді
х • 4 = 160
х = 160 : 4
х = 40
Відповідь: Віктор використав на кожну фігуру 40 деталей.
Інші завдання дивись тут...
