Завдання 753
1) кут, який дорівнює 50°, гострий; Істинне
2) кут, який дорівнює 86°, тупий; Хибне
3) кут, який дорівнює 92°, прямий; Хибне
4) кут, який дорівнює 115°, тупий; Істинне
5) кут, який дорівнює 91°, гострий; Хибне
6) кут, який дорівнює 180°, розгорнутий? Істинне.
Завдання 754 Види кутів
Кут 27° гострий, 90° прямий, 139° тупий, 180° розгорнутий, 89° гострий, 161° тупий.
Завдання 755
|
1) ∠M = 42° гострий
2) ∠N = 90° прямий
3) ∠O = 113° тупий
4) ∠P = 7° гострий
|
5) ∠R = 97° тупий
6) ∠S = 81° гострий
7) ∠T = 180° розгорнутий
8) ∠Q = 178° тупий
|
Завдання 756
1) ∠АОК = 30°; ∠AOL = 70°; ∠АОМ = 120°; ∠AON = 140°;
2) ∠ВОN = 40°; ∠ВОМ = 60°; ∠ВОL = 110°; ∠ВОК = 150°.
Завдання 757 За допомогою транспортира виміряй кути.
∠А = 60°, ∠М = 90°, ∠К = 105°, ∠В = 35°, ∠С = 125°
Завдання 758
∠К = 125°, ∠А = 80°, ∠F = 90°, ∠L = 100°, ∠M = 50°
Завдання 759
1) Градусні міри кутів: ∠АОВ = 65°, ∠АОМ = 30°, ∠ВОМ = 35°
2) Обчислили: ∠АОМ + ∠МОВ = 30° + 35° = 65°
3) Висновок: ∠АОВ = ∠АОМ + ∠ВОМ, тобто градусна міра початкового кута дорівнює сумі градусних мір кутів, на які його поділено.
Завдання 760
1) Градусні міри кутів: ∠CОN = 35°, ∠NОD = 75°, ∠CОD = 110°
2) Обчислили: ∠COD – ∠CON = 110° – 35° = 75°
3) Висновок: ∠NОD = ∠СОD – ∠CОN, тобто градусна міра одного з поділених кутів, дорівнює різниці початкового кута та іншого поділеного кута.
Завдання 761
Накресли в зошиті гострий і тупий кути. Виміряй їх за допомогою транспортира та запиши результат.
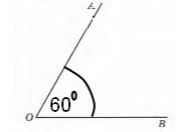 |
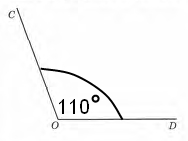 |
| ∠АОВ = 60° | ∠COD = 110° |
Завдання 762
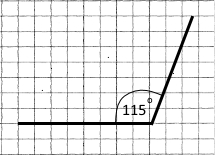
Накресліть кути, градусна міра яких дорівнює заданому числу.
| 1) 30° | 2) 180° | 3) 115° |
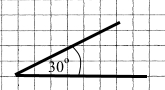 |
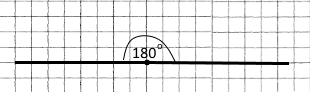 |
 |
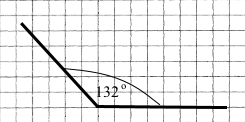
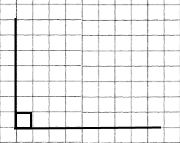
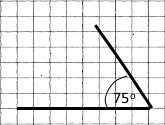
| 4) 132° | 5) 90° | 6) 75° |
 |
 |
 |
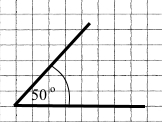
Завдання 763
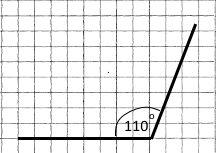
| 1) 50° | 2) 110° |
 |
 |
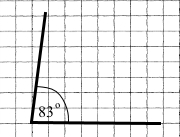
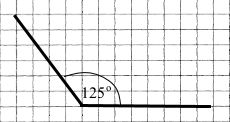
| 3) 83° | 4) 125° |
 |
 |
Завдання 764
∠СОВ = ∠АОВ – ∠АОС = 180° – 70° = 110°
Завдання 765
∠DOC = ∠АОВ – (∠АОD + ∠СОВ) = 180° – (60° + 55°) = 180° – 115° = 65°
Завдання 766
∠АОВ = ∠АОС – ∠ВОС = 90° – 30° = 60°
Завдання 767 Знайди градусну міру кута AOC, якщо ∠AOB — прямий.
Для малюнка 21.9:
∠АОС = ∠ВОК – ∠АОВ – ∠СОК = 180° – (90° + 60°) = 180° – 150° = 30°
Для малюнка 21.10:
∠АОС = ∠АОВ – ∠ВОС = 90° – 40° = 50°
Завдання 768
Промінь ОK ділить кут AOB на два кути: АОK і KОВ. Знайди градусну міру кута AOB, якщо ∠AOK = 52°, ∠KОВ = 43°.
∠АОВ = ∠АОК + ∠КОВ = 52° + 43° = 95°
Відповідь: ∠АОВ = 95°
Завдання 769
Промінь ON ділить кут AOB на два кути: AON і NOB. Знайди градусну міру кута AOB, якщо ∠AON = 37°, ∠NOB = 59°.
∠АОВ = ∠АОN + ∠NОВ = 37° + 59° = 96°
Відповідь: ∠АОВ = 96°
Завдання 770
1) Побудуй кут AOB, який дорівнює 120°.
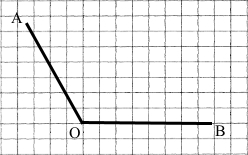
2) Проведи промінь OC так, щоб кут AOC дорівнював 30° (два способи).
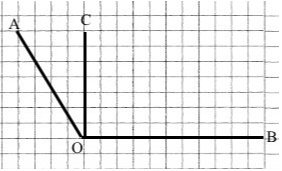 |
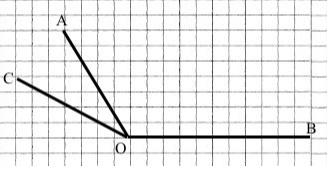 |
|
3) Знайди градусну міру кута BOC, що утворився. |
|
|
∠ВОС = ∠AOB – ∠AOC = 120° – 30° = = 90° Відповідь: ∠ВОС = 90°. |
∠ВОС = ∠AOB + ∠AOC = 120° + 30° =
= 150°
Відповідь: ∠ВОС = 150°.
|
Завдання 771
1) Побудуй кут COD, який дорівнює 70°.
2) Проведи промінь OM так, щоб кут COM дорівнював 40° (два способи).
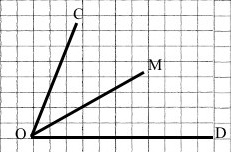 |
 |
| 3) Знайди градусну міру кута MOD, що утворився. | |
|
∠MОD = ∠СОD – ∠CОM = 70° – 40° =
= 30°
Відповідь: ∠MОD = 30°.
|
∠MОD = ∠CОD + ∠CОM = 70° + 40° =
= 110°
Відповідь: ∠MОD = 110°.
|
Завдання 772
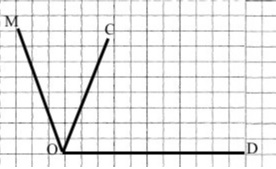
1) У яку ціль влучить кулька, якщо удар по ній від точки відліку (0°) спрямовано:
а) на 90° — в ціль D.
б) на 150° — в ціль F.
в) на 30° — в ціль B.
2) Скільки градусів між цілями:
а) деревом і ялинкою; 120° – 60° = 60°
б) ялинкою і будинком A; 60° – 0° = 60°
в) ялинкою і будинком G; 180° – 60° = 120°
г) будинком A і будинком F? 150° – 0° = 150°
Завдання 773
Знайди градусну міру кута між стрілками годинника, якщо він показує:
360° : 12 = 30° або 180° : 6 = 30° – міра кута, що припадає на 1 год.
 |
 |
| 1) 1 год; З0° • 1 = 30° | 4) 5 год; 30° • 5 = 150° |
 |
 |
|
2) 2 год; З0° • 2 = 60°
|
5) 8 год; З0° • 8 = 240°
|
 |
 |
|
3) 3 год; З0° • 3 = 90°
|
6) 10 год. З0° • 10 = 300°
|
Завдання 774
Виміряли кут: ∠АОС = 130°.
Дано: ∠АОС = 130°, ∠АОК = 90°, ∠АОМ = 180°
Розв’язання
∠КОС = ∠АОС – ∠АОК = 130° – 90° = 40°
∠СОМ = ∠АОМ – ∠АОС =180° – 130° = 50°
Відповідь: ∠КОС = 40°, ∠СОМ = 50°.
Завдання 775
Виміряли кут: ∠АОК = 50°.
Дано: ∠АОК = 50°, ∠АОС = 90°, ∠АОВ = 180°
Розв’язання
∠КОВ = ∠АOВ – ∠АОК = 180° – 50° = 130°
∠АОС = ∠СOВ = 90°
Відповідь: ∠КОВ = 130°, ∠АОС =90°.
Завдання 776
Прямий кут AOB (мал. 21.14) поділено променями OC і OD так, що ∠AOD = 60°, ∠BOC = 70°. Знайди градусну міру кута COD.
Розв’язання
1) ∠BОD = ∠АОВ – ∠АОD = 90° – 60° = 30°
2) ∠AОC = ∠AОВ – ∠BОC = 90° – 70° = 20°
3) ∠CОD = ∠AОВ – (∠AОC + ∠BОD) = 90° – (30° + 20°) = 40°
Відповідь: ∠CОD = 40°.
Завдання 777
Розгорнутий кут COD поділено променями ON і OF так, що ∠NOD = 130°, ∠COF = 110° (мал. 21.15). Знайди градусну міру кута NOF.
Розв’язання
1) ∠CОN = ∠CОD – ∠DON = 180° – 130° = 50°
2) ∠FОD = ∠CОD – ∠COF = 180° – 110° = 70°
3) ∠NОF = ∠CОD – (∠FОD + ∠CОN) = 180° – (70° + 50°) = 60°
Відповідь: ∠NОF = 60°.
Завдання 778
Кут MOK втричі менший від кута KON (мал. 21.16). Знайди ці кути, якщо ∠MON = 140°.
Розв’язання
1 спосіб
Нехай ∠МОК дорівнює х°, тоді ∠КОN дорівнює 3х°, а їх сума дорівнює 140°. Складаємо рівняння.
х + 3х = 140
4х = 140
х = 140 : 4
х = 35 (°) – градусна міра ∠МОК;
35 • 3 = 105 (°) – градусна міра ∠KON.
2 спосіб
1) 1 + 3 = 4 (ч.) – всього частин;
2) 140 : 4 = 35 (°) – градусна міра ∠MOK;
3) 35 • 3 = 105 (°) – градусна міра ∠KON.
Відповідь: ∠МОK = 35°, ∠KОN = 105°.
Завдання 779
Кут AOB удвічі менший від кута BOC (мал. 21.17). Знайди ці кути, якщо ∠AOC = 120°.
Розв’язання
1 спосіб
Нехай ∠АОВ дорівнює х°, тоді ∠ВОС дорівнює 2х°, а їх сума дорівнює 120°. Складаємо рівняння.
х + 2х = 120
3х = 120
х = 120 : 3
х = 40 (°) – градусна міра ∠АОВ.
40 • 2 = 80 (°) – градусна міра ∠ВОС.
2 спосіб
1) 1 + 2 = 3 (ч.) – всього частин;
2) 140 : 3 = 40 (°) – градусна міра ∠АОВ;
3) 40 • 2 = 80 (°) – градусна міра ∠ВОС.
Відповідь: ∠АОВ = 40°, ∠ВОС = 80°.
Завдання 780
Накресли пряму AB і познач на ній точку O. Потім побудуй кут AOC, який дорівнює 120°, і кут BOD, який дорівнює 35° (двома способами). Обчисли градусну міру кутів COB і COD.
1 випадок:
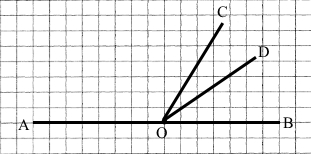
∠СОВ = ∠AOB – ∠AOC = 180° – 120° = 60°
∠СОD = ∠COB – ∠DOB = 60° – 35° = 25°
Відповідь: ∠ СОВ = 60°, ∠СОD= 25°.
2 випадок:
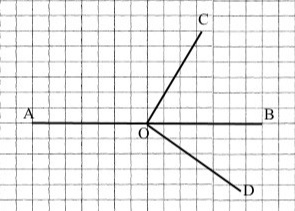
∠COB = ∠AOB – ∠AOC = 180° – 120° = 60°
∠СОD = ∠COВ – ∠DOB = 60° + 35° = 95°
Відповідь: ∠СОВ = 60°, ∠СОD = 95°
Завдання 781
З вершини прямого кута проведено промінь так, що він ділить прямий кут на два кути, градусна міра одного з яких на 10° більша за міру іншого. Знайди градусну міру кожного із цих двох кутів.
Розв’язання
1 спосіб
Нехай перший кут дорівнює х°, тоді другий кут дорівнює (х + 10)°, а їх сума дорівнює 90°. Складаємо рівняння.
х + (х + 10) = 90
2х = 90 – 10
2х = 80
х = 80 : 2
х = 40 (°) – градусна міра одного кута;
40 + 10 = 50 (°) – градусна міра іншого кута.
2 спосіб
1) 90 – 10 = 80 (°) – градусна міра двох кутів порівно;
2) 80 : 2 = 40 (°) – градусна міра одного кута;
3) 40 + 10 = 50 (°) – градусна міра другого кута.
Відповідь: перший кут дорівнює 40°, а другий кут дорівнює 50°.
Завдання 782 Не розв’язуючи рівняння, знайди, яке із чисел 5, 6, 7 або 8 є коренем рівняння:
1) 5(5 – 2) + 4 = 24, 5 • 3 + 4 ≠ 24, число 5 не є коренем рівняння.
5(6 – 2) + 4 = 24, 5 • 4 + 4 = 20 + 4 = 24, число 6 є коренем рівняння.
5(7 – 2) + 4 = 24, 5 • 5 + 4 ≠ 24, число 5 не є коренем рівняння.
5(8 – 2) + 4 = 24, 5 • 6 + 4 ≠ 24, число 8 не є коренем рівняння.
2) 12 – 3(5 – 5) = 6, 12 – 3 • 0 ≠ 6, число 5 не є коренем рівняння.
12 – 3(6 – 5) = 6, 12 – 3 • 1 ≠ 6, число 6 не є коренем рівняння.
12 – 3(7 – 5) = 6, 12 – 3 • 2 = 12 – 6 = 6, число 7 є коренем рівняння.
12 – 3(8 – 5) = 6, 12 – 3 • 3 ≠ 6, число 8 не є коренем рівняння.
3) 12 + 3(5 + 7) = 57, 12 + 3 • 12 ≠ 57, число 5 не є коренем рівняння.
12 + 3(6 + 7) = 57, 12 + 3 • 13 ≠ 57, число 6 не є коренем рівняння.
12 + 3(7 + 7) = 57, 12 + 3 • 14 ≠ 57, число 7 не є коренем рівняння.
12 + 3(8 + 7) = 57, 12 + 3 • 15 = 12 + 45 = 57, число 8 є коренем рівняння.
4) 9(5 + 3) – 12 = 60, 9 • 8 – 12 = 72 – 12 = 60, число 5 є коренем рівняння.
9(6 + 3) – 12 = 60, 9 • 9 – 12 ≠ 60, число 6 не є коренем рівняння.
9(7 + 3) – 12 = 60, 9 • 10 – 12 ≠ 60, число 7 не є коренем рівняння.
9(8 + 3) – 12 = 60, 9 • 11 – 12 ≠ 60, число 8 не є коренем рівняння.
Завдання 783
Як зміниться сума чисел 2317 і 5372, якщо до першого числа додати 712, а до другого — 611?
(2317 + 712) + (5372 + 611) = (2317 + 5372) + (712 + 611)
Сума збільшиться на суму чисел 712 та 611, тобто на 712 + 611 = 1323.
Відповідь: збільшиться на 1323.
Завдання 784 Заповни комірки в ланцюжку.
1) 12 хв • 25 = 300 хв = (300 : 60) год = 5 год; 5 год + 7 год = 12 год
2) 16 діб : 2 = 8 діб; 8 діб – 17 год = 7 діб + 24 год – 17 год = 7 діб 7 год
3) 16 с • 150 = 2400 с; 2400 с + 13 хв = (2400 : 60) хв + 13 хв = 40 хв + 13 хв = 53 хв
4) 15 хв : 90 = 15 • 60 с : 90 = 900 с : 90 = 100 с; 100 с + 5 с = 105 с
Завдання 785
Василь щодня витрачає 20 грн на проїзд до роботи і стільки само назад. Він вирішив їздити туди й назад на велосипеді. Скільки грошей заощадить Василь за тиждень? Чи зможе він через місяць (22 робочих дні) на заощаджені гроші придбати велосипедний шлем вартістю 890 грн?
Розв’язання
1) 20 • 2 = 40 (грн) – витрачає грошей за день;
2) 40 • 7 = 280 (грн) – заощадить грошей за 7 днів;
3) 40 • 22 = 880 (грн) – заощадить грошей за місяць (22 робочі дні).
880 грн < 890 грн
Відповідь: 280 грн, не зможе.
Завдання 786 Письмове множення і письмове ділення
|
х 125
98
1000
1125
12250
|
_408 | 24 24 17 _168 168 0 |