ГДЗ Скворцова Математика 4 клас сторінка 54

Інші завдання дивись тут...

© Барна Р., 2021

Серія "Вчимось разом" до підручника

"Математика 4 клас Скворцова С., Онопрієнко О."

Сторінка 54

Завдання 1 Застосували розподільний закон множення відносно додавання, переставний закон додавання:

67 • 5 = (60 + 7) • 5 = 60 • 5 + 7 • 5 = 300 + 35 = 335

8 • 79 = 79 • 8 = (70 + 9) • 8 = 70 • 8 + 9 • 8 = 560 + 72 = 632

Завдання 2, 3

Значення перших двох добутків допомогли знайти значення третього добутку:

42 • 4 = (40 + 2) • 4 = 168

42 • 20 = (40 + 2) • 20 = 840

42 • 24 = 42 • (20 + 4) = 42 • 20 + 42 • 24 = 840 + 168 = 1008

х 42

168

1008

36 • 8 = (30 + 60) • 8 = 288

36 • 10 = 360

36 • 18 = 36 • (10 + 8) = 36 • 10 + 36 • 8 = 360 + 288 = 648

х36

288

648

27 • 2 = 27 + 27 = 54

27 • 30 = (20 + 7) • 30 = 810

27 • 32 = 27 • (30 + 2) = 27 • 30 + 27 • 2 = 810 + 54 = 864

х 27

864

Сторінка 55

Завдання 4 Письмове множення

х28

896

х56

392

952

х 32

256

896

х43

946

Завдання 5 Письмове ділення

Ділення

_720 | 30

60 24

_120

120

_960 | 60

60 16

_360

360

_850 | 50

50 17

_350

350

_540 | 30

30 18

_240

240

Перевірка

множенням

х24

720

х16

960

х17

850

х18

540

Завдання 6 Обернені задачі про продуктивність праці

_{1) Задача на послідовне ділення (завжди має два способи розв’язування)}

За 6 годин 3 робітники уклали 54 м тротуарної плитки з однаковою продуктивністю праці. Скільки метрів плитки укладає робітник щогодини?

^{Плиток 1 роб. за 1 год}	^{Кількість годин}	^{Кількість робітників}	^{Загальний виробіток}
^?	⁶	³	^{54 м}

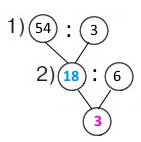
^{1 спосіб}

^{Короткий запис}

^{3 р. — 6 год — 54 м}

^{1 р. — 6 год —}^?^м

^{1 р. — 1 год —}^?^м

^Схема

^{Вираз 54 : 3 : 6}

Розв’язання

1) 54 : 3 = (30 + 24) : 3 = 18 (м) – метрів плитки укладає робітник за 6 годин.

2) 18 : 6 = 3 (м) – метрів плитки укладає робітник щогодини.

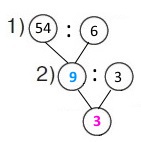
^{2 спосіб}

^{Короткий запис}

^{3 р. — 6 год — 54 м}

^{3 р. — 1 год —}^?^м

^{1 р. — 1 год —}^?^м

^Схема

^{Вираз 54 : 6 : 3}

Розв’язання

1) 54 : 6 = 9 (м) – метрів плитки укладають 3 робітники щогодини.

2) 9 : 3 = 3 (м) – метрів плитки укладає робітник щогодини.

Відповідь: щогодини робітник укладає 3 метри тротуарної плитки.

_{2) Задача на послідовне множення (завжди має декілька способів розв’язування)}

Щогодини робітник укладає 3 м тротуарної плитки. Скільки метрів плитки укладають 3 робітників за 6 год, якщо вони працюватимуть з однаковою продуктивністю?

^{Плиток 1 роб. за 1 год}	^{Кількість годин}	^{Кількість робітників}	^{Загальний виробіток}
^{3 м}	⁶	³	^?

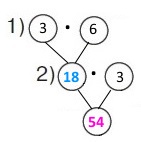
^{1 спосіб}

^{Короткий запис}

^{1 р. — 1 год. — 3 м}

^{1 р. — 6 год —}^?^м

^{3 р. — 6 год —}^?^м

^Схема

^{Вираз 3 • 6 • 3}

Розв’язання

1) 3 • 6 = 18 (м) – метрів плитки укладає робітник за 6 годин.

2) 18 • 3 = (10 + 8) • 3 = 54 (м) – метрів плитки укладають 3 робітників за 6 годин.

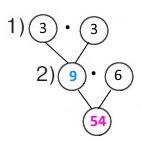
^{2 спосіб}

^{Короткий запис}

^{1 р. — 1 год. — 3 м}

^{3 р. — 1 год —}^?^м

^{3 р. — 6 год —}^?^м

^Схема

^{Вираз 3 • 3 • 6}

Розв’язання

1) 3 • 3 = 9 (м) – метрів плитки укладають 3 робітників щогодини.

2) 9 • 6 = 54 (м) – метрів плитки укладають 3 робітників за 6 годин.

Відповідь: укладають 54 метри тротуарної плитки.

Сторінка 56

Завдання 1

_{1) Задача на зведення до одиниці}

На добу 3 кролям треба 330 г сухого корму. Скільки грамів корму треба на добу 9 кролям?

^{1 спосіб (зведення до одиниці)}

^{Короткий запис}

^{3 кролі — 330 г}

^{9 кролів — ? г}

^{План розв’язування}

^{1) Скільки грамів корму треба на добу кролю?}

^{2) Скільки грамів корму треба на добу 9 кролям?}

Розв’язання

1) 330 : 3 = 110 (г) — корму треба на добу кролю.

2) 110 • 9 = 990 (г) — кормів треба на добу 9 кролям.

^{2 спосіб (відношень)}

^{Короткий запис}

^{3 кролі — 330 г}

^{9 кролів — ? г}

^{План розв’язування}

^{1) У скільки разів більше кролів?}

^{2) Скільки грамів корму треба на добу 9 кролям}^?

Розв’язання

1) 9 : 3 = 3 (рази) – у стільки разів більше кролів.

2) 330 • 3 = 990 (г) — кормів треба на добу 9 кролям.

^{3 спосіб (рівняння для зведення до одиниці)}

^{Короткий запис}

^{3 кролі — 330 г}

^{9 кролів — х г}

^{Нехай х (г) – кормів треба, тоді 330 : 3 (г) – кормів треба кролю на добу, а також х : 9 (г) – кормів треба кролю на добу, тому складемо рівняння}

х : 9 = 330 : 3

х : 9 = 110

х = 110 • 9 = 990 (г) – кормів треба на добу 9 кролям.

^{4 спосіб (рівняння для відношень)}

^{Короткий запис}

^{3 кролі — 330 г}

^{9 кролів — х г}

^{Нехай х (г) – кормів треба, тоді 9 : 3 (разів) – у стільки разів більше кролів, а також х : 330 (разів) – у стільки разів більше кормів, тому складемо рівняння}

х : 330 = 9 : 3

х : 330 = 3

х = 3 • 330 = 990 (г) – кормів треба на добу 9 кролям.

Відповідь: треба 990 г кормів.

_{2) Задача на послідовне ділення}

На 2 доби 3 кролям треба 660 г сухого корму. Скільки грамів корму треба на добу 1 кролю?

^{Маса корму 1 кролю на 1 добу}	^{Кількість діб}	^{Кількість кролів}	^{Загальна маса корму}
^?	²	³	^{660 г}

^{1 спосіб}

^{Короткий запис}

^{3 кр. — 2 доби — 660 г}

^{1 кр. — 2 доби —}^?^м

^{1 кр. — 1 доба —}^?^м

^{Вираз 660 : 3 : 2}

Розв’язання

1) 660 : 3 = 220 (г) – корму треба кролю на 2 доби.

2) 220 : 2 = 110 (г) – корму треба кролю на добу.

^{2 спосіб}

^{Короткий запис}

^{3 кр. — 2 доби — 660 г}

^{3 кр. — 1 доба —}^?^м

^{1 кр. — 1 доба —}^?^м

^{Вираз 660 : 2 : 3}

Розв’язання

1) 660 : 2 = 330 (г) – корму треба 3 кролям на добу.

2) 330 : 3 = 110 (г) – корму треба кролю на добу.

Відповідь: на добу кролю треба 110 г корму.

_{3) Складена задача на знаходження суми добутків}

Дорослому кролю на добу треба 110 г сухого корму, а маленькому — 50 г. Скільки грамів корму треба дорослому кролю та кроленяті разом на 2 доби?

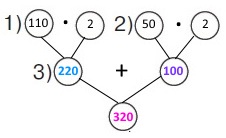
^{1 спосіб}

^{Короткий запис}

^{Дорослому —}^?^{г, 2 доби по 110 г}

^{Маленькому —}^?^{г, 2 доби по 50 г}

^{Всього —}^?

^Схема

^{Вираз 110 • 2 + 50 • 2}

Розв’язання

1) 110 • 2 = 220 (г) – корму треба дорослому кролю на 2 доби.

2) 50 • 2 = 100 (г) – корму треба кроленяті на добу.

3) 220 + 100 = 320 (г) – всього корму треба на 2 доби.

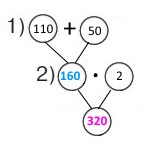
^{2 спосіб}

^{Оскільки однакова кількість діб, тому}

^{Короткий запис}

^{Корми —}^{? г, 2 доби по}^?^{(110 г і 50 г)}

^Схема

^{Вираз (110 + 50) • 2}

Розв’язання

1) 110 + 50 = 160 (г) – всього корму треба на добу.

2) 160 • 2 = 320 (г)– всього корму треба на 2 доби.

Відповідь: треба 320 г корму.

Завдання 2

х38

114

874

х46

414

874

х41

164

984

х36

216

936

Завдання 3 Рівняння

⁵⁶⁰^{: 40 + k = 23}

^{(400 + 160) : 40 + k = 23}

^{14 + k = 23}

^{k = 23 – 14}

^{k = 9}

^{560 : 40 + 9 = 23}

^{23 = 23}

^{n – 480 = 48 • 20}

^{n – 480 = (40 + 8) • 20}

^{n – 480 = 960}

^{n = 960 + 480}

^{n = 1300 + 140}

^{n = 1440}

^{1440 – 480 = 1440 – 500 + 20 = 960}

^{48 • 20 = 960}

^{960 = 960}

^{a : 60 = 840 : 70}

^{a : 60 = (700 + 140) : 70}

^{a : 60 = 12}

^{a = 12 • 60}

^{a = (10 + 2) • 60}

^{a = 720}

^{720 : 60 = (600 + 120) : 60 = 12}

^{840 : 70 = 12}

^{12 = 12}

Завдання 4 Побудуй прямокутник зі сторонами 55 мм і 45 мм, обчисли його периметр. Побудуй квадрат із таким периметром.

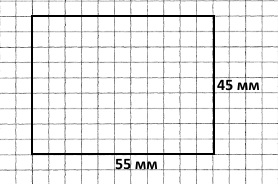
Р = (55 + 45) • 2 = 100 • 2 = 200 (мм) = 20 (см) – периметр прямокутника (також квадрата).

20 : 4 = 5 (см) – довжина сторони квадрата.

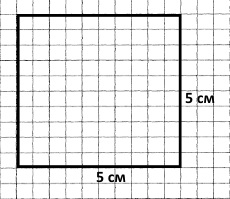
Завдання 5 Складена задача на знаходження частини числа

У сухому кормі для кролів борошно з трави становить третину всієї маси, зерно пшениці — п'яту частину, дріжджі — соту частину. Скільки окремо грамів дріжджів, борошна та зерна пшениці міститься в 900 г корму?

^{Короткий запис}

^{Дріжджі —}^?^{г, 1/100 від всього}

^{Борошно — ? г, 1/3 від всього}

^{Зерно — ? г, 1/5 від всього}

^{Всього — 900 г}

Розв’язання

1) 900 : 100 = 9 (г) – дріжджів.

2) 900 : 3 = 300 (г) – борошна.

3) 900 : 5 = (500 + 400) : 5 = 180 (г) – зерна.

Відповідь: дріжджів – 9 г, борошна – 300 г, зерна – 180 г.

Завдання 6 Якщо олією з бака наповнити 4 однакові банки, то в баці залишиться 24 л олії, а якщо наповнити 6 таких банок, то в баці залишиться 18 л олії. Визнач місткість банки.

^{Короткий запис №1}

^{Було — однаково}

^{Розлили — 4 банки по ? л}

^{Залишилося — 24 л}

^{Короткий запис №2}

^{Було — однаково}

^{Розлили — 6 банок по ? л}

^{Залишилося — 18 л}

Розв’язання

1) 24 – 18 = 6 (л) – різниця літрів.

2) 6 – 4 = 2 (б.) – банок на 6 літрів олії.

3) 6 : 2 = 3 (л) – місткість банки.

^{2 спосіб (рівняння)}

	^{Було (однаково)}	^{Розлили}	^{Залишилося}
^І	^{24 + х • 4}	^{4 банки по х л}	^{24 л}
^ІІ	^{18 + х • 6}	^{6 банок по х л}	^{18 л}

^{Якщо х (л) – місткість банки, тоді х • 4 + 24 (л) – літрів олії було в бочці, а також х}^{• 6 + 18 (л) – літрів олії було в бочці. Складемо рівняння}

х • 4 + 24 = х • 6 + 18

х • 6 + 18 = х • 4 = 24

х • 6 – х • 4 = 24 – 18

х • 2 = 6

х = 6 : 2 = 3 (л) – місткість банки.

Відповідь: місткість банки 3 літри.

Сторінка 57

Завдання 1

_{1) Задачу на зведення до одиниці не можна розв’язати способом відношень}

За 4 год майстриня пошила 16 м'яких іграшок. Скільки таких іграшок вона пошиє за 5 год, якщо працюватиме з тією самою продуктивністю?

^{1 спосіб (зведення до одиниці)}

^{Короткий запис}

^{4 год — 16 іг.}

^{5 год — ? іг.}

Розв’язання

1) 16 : 4 = 4 (іг.) – іграшок пошила за годину.

2) 4 • 5 = 20 (іг.) – іграшок пошиє за 5 годин.

^{2 спосіб (рівняння для зведення до одиниці)}

^{Короткий запис}

^{4 год — 16 іг.}

^{5 год — ? іг.}

^{Нехай х (іг.) – іграшок пошиє, тоді 16 : 4 (іг.) – іграшок пошиє за годину, а також х : 5 (іг.) – іграшок пошиє за годину, тому складемо рівняння}

х : 5 = 16 : 4

х : 5 = 4

х = 4 • 5 = 20 (іг.) – іграшок пошиє за 5 годин.

Відповідь: майстриня пошиє 20 іграшок.

_{2) складена на множення}

Дві майстрині за 4 год пошили 32 м'які іграшки. Скільки таких іграшок пошиє одна майстриня за 5 год, якщо обидві майстрині працюють з однаковою продуктивністю?

^{Іграшок 1 майстриня за 1 год}	^{Кількість год}	^{Кількість майстринь}	^{Загальна кількість іграшок}
^?	⁴	²	^{32 іграшки}
^{однаково}	⁵		^?

^{1 спосіб}

^{Короткий запис}

^{2 м. — 4 год — 32 іг.}

^{1 м. — 4 год —}^?^іг.

^{1 м. — 1 год —}^?^іг.

^{1 м. — 5 год —}^?^іг.

^{Вираз (32 : 2 : 4) • 5}

Розв’язання

1) 32 : 2 = 16 (іг.) – іграшок шиє майстриня за 4 год.

2) 16 : 4 = 4 (іг.) – іграшок шиє майстриня щогодини.

3) 4 • 5 = 20 (іг.) – іграшок пошиє майстриня за 5 год.

^{2 спосіб}

^{Короткий запис}

^{2 м. — 4 год — 32 іг.}

^{2 м. — 1 год —}^?^іг.

^{1 м. — 1 год —}^?^іг.

^{1 м. — 5 год —}^?^іг.

^{Вираз (32 : 4 : 2) • 5}

Розв’язання

1) 32 : 4 = 8 (іг.) – іграшок шиють 2 майстрині щогодини.

2) 8 : 2 = 4 (іг.) – іграшок шиє майстриня щогодини.

3) 4 • 5 = 20 (іг.) – іграшок пошиє майстриня за 5 год.

Відповідь: майстриня пошиє 20 іграшок.

Сторінка 58

Завдання 2 Складена задача на множення

Два асфальтоукладачі за 4 год роботи уклали 32 м дороги. Скільки метрів дороги укладе один асфальтоукладач за 5 год, якщо машини працюють з однаковою продуктивністю?

^{Довжина 1 асфальтоукладач за 1 год}	^{Кількість год}	^{Кількість асфальтоукладачів}	^{Загальна довжина}
^?	⁴	²	^{32 м}
^{однаково}	⁵		^?

Змінилися описові дані (одиниці вимірювання, замість майстринь – роботу виконують асфальтоукладачі), а числові дані не змінилися.

Оскільки числові дані однакові, то розв’язується аналогічно задачі 2 зі завдання 1.

Завдання 3 Складена задача на множення. Змінилися числові дані.

Три асфальтоукладачі за 2 год роботи укладають 42 м дороги. Скільки метрів дороги укладе один асфальтоукладач за 4 год, якщо машини працюють з однаковою продуктивністю?

^{Довжина 1 асфальтоукладач за 1 год}	^{Кількість год}	^{Кількість асфальтоукладачів}	^{Загальна довжина}
^?	²	³	^{42 м}
^{однаково}	⁴		^?