Інші завдання дивись тут ...

© ГДЗ 8next.com, 2013, 2018, 2022

Запитання

1. Що називають добутком числа а на натуральне число b, яке не дорівнює 1?

Добутком числа а на натуральне число b, яке не дорівнює 1, називають суму, що складається з Ь доданків, кожний з яких дорівнює а.

2. Як у рівності а • b = с називають число а? число b? число с? запис а • b?

Число а - множник, б - множник, с - добуток.

Запис а • b називають добутком чисел а і b.

3. Чому дорівнює добуток двох множників, один з яких дорівнює 1?

а • 1 = 1 • а = а

4. Чому дорівнює добуток двох множників, один з яких дорівнює 0?

а • 0 = 0 • а = 0

5. У якому випадку добуток може дорівнювати нулю?

Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю.

6. Сформулюйте переставну властивість множення.

Від перестановки множників добуток не змінюється.

7. Як записують у буквеному вигляді переставну властивість множення?

ab = Ьа

 

Розв'язуємо усно

Завдання 1

1) 20 + 20 + 20 = 20 • 3 = 60

2) 12 + 12 + 12 + 12 = 12 • 4 = 48

3) 7 + 7 + 7 + 7 + 7 = 7 • 5 = 35

 

Завдання 2

1) 6 + 4 • 3 ‒ 2 = 6 + 12 ‒ 2 = 16 

2) (6 + 4) • 3 ‒ 2 = 10 • 3 ‒ 2 = 30 ‒ 2 = 28

3) 6 + 4 • (3 ‒ 2) = 6 + 4 • 1 = 10

4) (6 + 4) • (3 ‒ 2) = 10 • 1 = 10

 

Завдання 3 Письмове множення чисел 14 і 6 .

х 14

     6

   84

 

Завдання 4 Збільште число 18 у 3 рази.

х 18

     3

   54

 

Завдання 5 Знайдіть бічну сторону рівнобедреного трикутника, якщо його периметр на 12 см більший за основу.

Розв'язання

12 : 2 = 6 (см)

Відповідь: бічна сторона рівнобедреного трикутника дорівнює 6 см.

 

Завдання 6 Визначте вид трикутника, дві сторони якого дорівнюють 8 см і 12 см, а периметр — 28 см.

Розв'язання

1) 8 + 12 = 20 (см) ‒ сума двох сторін трикутника.

2) 28 ‒ 20 = 8 (см) ‒ третя сторона трикутника.

Отже, маємо трикутник у якого дві сторони дорівнюють 8 см, тому  трикутник - рівнобедрений. 

 

Завдання 7 Знайдіть периметр квадрата, якщо він більший за його сторону на 18 см.

Розв'язання

1) 18 см : 3 = 6 см ‒ довжина сторони квадрата.

2) 6 см • 4 = 24 см

Відповідь: периметр квадрата 24 см.

 

Завдання 8

1) a • 5 = a для а = 0 (0 • 5 = 0)

2) a • 1 = a для а = 1 (1 • 1 = 1)

3) a • a = a для а = 0, 1 (0 • 0 = 0, 1 • 1 = 1)

4) 0 • a = a хибне, бо 0 • а = 0

 

Вправи

Вправа 415° Запишіть суму у вигляді добутку:

1) 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 6 • 8 

2) 9 + 9 + 9 + 9 + 9 = 9 • 5 

3 ) n + n + n + n + n + n + n = n • 7 

4) 2 + 2 + ... + 2 (всього 101 доданок) = 2 • 101 

5) 5 + 5 + ... + 5 (всього m доданків) = 5 • m

6) m + m +... + m (всього k доданків) = m • k

 

Вправа 416° 

х   516       32    1032  1548     16512	х   314      258    2512  1570  628       81012	х   1234       567     8638   7404  6170     699678
х   4519         52      9038   22595     234988	х   215     204     860  430      43860	х     2984        4006      17904 11936      11953904

Вправа 417°

х  706      53   2118  3530    37418	х    591       289     5319   4728  1182      170799	х  2468      359   22212 12340 7404    886012
х  5245        67   36715 31470   351415	х   465      506    2790 2325   235290	х   1234      2007      8638 2468      2476638

Вправа 418° Знайдіть число, яке:

1) у 46 разів більше за число 418;	2) у 3000 разів більше за число 270
х  418      46   2508 1672   19228	х 270     3000   810000

 

Вправа 419°

1) 17х + 432, якщо х = 58;

2) (739 ‒ х) • у, якщо х = 554, у = 4900.

Розв'язання

1) якщо х = 58, тоді 17х + 432 = 17 • 58 + 432 = 1418

2) якщо х = 554, у = 4900, тоді (739 ‒ х) • у = (739 ‒ 554) • 4900 = 906500

х  17    58   136   85     986

+986   432  1418

_739  554  185

х185     4900 1665 740      906500

Вправа 422°

1) 976 ‒ 24х, якщо х = 36;

2) х • 63 — у, якщо х = 367, у = 19 742.

Розв'язання

1) якщо х = 36, тоді 976 ‒ 24х = 976 ‒ 24 • 36 = 112

2) якщо х = 367, у = 19742, тоді х • 63 ‒ у = 367 • 63 ‒ 19742 = 3379

х 24   36 144 72   864

_ 976   864   112

х   367       63    1101   2202     23121

_23121  19742   3379

Вправа 423° (Домашня практична робота) У записі 133 • 908 = МВСАОО буквами позначено цифри числа, що є результатом множення. Із цих букв складається прізвище видатного українського лікаря. Щоб розшифрувати слово, достатньо в наведеній таблиці під кожною цифрою записати літеру, яка стоїть на місті цієї цифри в правій частині даного запису. Яке прізвище цього лікаря? 

Розв’язання

1) 25 • 12 = 300 (мг) – вітаміну С краде у себе курець.

2) 500 – 300 = 200 (мг) – вітаміну надходитиме до організму курця.

Відповідь: 200 мг.

 

Вправа 425° Готуючись до школи, Буратіно купив 34 зошити по 12 сольдо і 18 зошитів по 16 сольдо. Скільки сольдо заплатив Буратіно за всі зошити?

^{Короткий запис}

^{34 з. по 12 с. — ?}

^{18 з. по 16 с. — ?}

^{Вартість — ?} 

Розв'язання

1) 12 • 34 = 408 (с.) ‒ заплатив за зошити по 12 сольдо.

2) 16 • 18 = 288 (с.) ‒ заплатив за зошити по 16 сольдо.

3) 288 + 408 = 696 (с.) ‒ заплатив за всі зошити.

Відповідь: за всі зошити Буратіно заплатив 696 сольдо.

 

Вправа 426° Кіт Матроскін продав 42 л молока по 96 к. за літр і 16 кг сиру по 2 грн (200 к.) за кілограм. Скільки грошей отримав Матроскін за свій товар?

^{Короткий запис}

^{42 л по 96 к. — ?}

^{16 кг по 200 к. — ?}

^{Вартість — ?} 

Розв'язання

1) 96 • 42 = 4032 (к.) ‒ грошей отримав за молоко.

2) 200 • 16 = 3200 (к.) ‒ грошей отримав за сир.

3) 4032 + 3200 = 7232 (к.) = 72 грн 32 к. ‒ грошей отримав за товар.

Відповідь: за свій товар кіт Матроскін отримав 72 грн 32 к.  

 

Завдання 427° За п’ять місяців (з травня по вересень) одна тополя поглинає 44 кг вуглекислого газу, а один дуб — 28 кг. На скільки більше кілограмів вуглекислого газу поглинають за цей період 40 тополь, ніж 40 дубів?

Розв’язання

1) 44 • 40 = 1760 (кг) – вуглекислого газу поглинають 40 тополь.

2) 28 • 40 = 1120 (кг) – вуглекислого газу поглинають 40 дубів.

3) 1760 – 1120 = 640 (кг)

Відповідь: на 640 кілограмів більше вуглекислого газу поглинають тополі, ніж дуби.

 

Вправа 428° Вирушивши в похід, Барвінок 14 год плив річкою на човні зі швидкістю 8 км/год і йшов пішки 23 год зі швидкістю 4 км/год. Який шлях, річкою чи суходолом, він подолав більший і на скільки кілометрів?

1) 8 • 14 = 112 (км) ‒ шлях річкою.

2) 4 • 23 = 92 (км) ‒ шлях пішки.

3) 112 ‒ 92 = 20 (км) ‒ на стільки довший шлях річкою.

Відповідь: шлях річкою на 20 км більший, ніж шлях пішки.

 

Вправа 429° Івасик‒Телесик плив на моторному човні 5 год річкою зі швидкістю 27 км/год і 7 год озером зі швидкістю 21 км/год. Який шлях, річкою чи озером, був довшим і на скільки кілометрів?

	Швидкість		Час	Загальна відстань
Річкою	27 км/год		5 год	?	На скільки ?
Озером	21 км/год		7 год	?

Розв'язання

1) 27 • 5 = 135 (км) ‒ шлях річкою.

2) 21 • 7 = 147 (км) ‒ шлях озером.

3) 147 ‒ 135 = 12 (км) ‒ на стільки довший шлях озером.

Відповідь: на 12 км довший шлях озером, ніж річкою.

 

Вправа 430 Порядок дій

1) (318 • 207 ‒ 64 934) • 276 + 604 • 88 = 299344
х   318     207   2226  636     65826	_65826  64934     892	х     892       276      5352    6244  1784     246192	х   604       88    4832   4832      53152	+246192    53152   299344
2) 869 • (61 124 ‒ 488 • 125) ‒ 509 • 74 = 70090
х  488    125   2440   976  488     61000	_61124  61000     124	х   869     124    3476   1738    869      107756	х   509      74   2036  3563    37666	_107756    37666    70090

Вправа 431

1) (214 • 104 + 7544) • 35 ‒ 508 • 722 = 676224
х  214     104     856  214     22256	+22256    7544   29800	х 29800     35  1490  894    1043000	х    508      722     1016   1016  3556     366776	_1043000    366776    676224
2) 647 • (36 900 ‒ 255 • 144) ‒ 318 • 92 = 87204
х  255    144   1020 1020 255    36720	_36900  36720     180	х  647      180   5176   647      116460	х 318     92    636 2862   29256	_116460    29256    87204

Вправа 432 З одного порту в інший одночасно відійшли теплохід і катер. Швидкість теплохода дорівнює 28 км/год, а швидкість катера — 36 км/год. Якою буде відстань між ними через 5 год після початку руху?

	Швидкість		Час	Відстань
Теплохід	28 км/год		5 год	?
Катер	36 км/год

Розв'язання

1) 36 ‒ 28 = 8 (км) ‒ на стільки збільшується відстань між теплоходом і катером щогодини.

2) 8 • 5 = 40 (км) ‒ відстань між теплоходом і катером через 5 год.

Відповідь: через 5 год від початку руху відстань між теплоходом і катером буде 40 км.

 

Вправа 433 З одного села в одному напрямі вирушили одночасно два велосипедисти. Один із них їхав зі швидкістю 12 км/год, а другий — зі швидкістю 9 км/год. Якою буде відстань між ними через 6 год після початку руху?

	Швидкість		Час	Відстань
I	12 км/год		6 год	?
II	9 км/год

Розв'язання

1) 12 ‒ 9 = 3 (км) ‒ на стільки збільшується відстань між велосипедистами щогодини.

2) 3 • 6 = 18 (км) ‒ відстань між велосипедистами через 6 год.

Відповідь: через 6 год від початку руху відстань між ними буде 18 км.

 

Вправа 434 З однієї станції в протилежних напрямах одночасно відійшли два поїзди. Один із них рухався зі швидкістю 64 км/год, а другий — зі швидкістю 57 км/год. Якою буде відстань між ними через 9 год після початку руху?

	Швидкість		Час	Відстань
I	64 км/год		9 год	?
II	57 км/год

Розв'язання

1) 64 + 57 = 121 (км) ‒ на стільки збільшується відстань між поїздами щогодини.

2) 121 • 9 = 1089 (км) ‒ відстань між поїздами через 9 год.

Відповідь: через 9 год від початку руху відстань між поїздами буде 1089 км.

 

Вправа 435 З одного міста в протилежних напрямах виїхали одночасно два автомобілі. Швидкість одного з них дорівнювала 74 км/год, що на 8 км/год більше, ніж швидкість другого. Якою буде відстань між ними через 7 год після початку руху?

	Швидкість		Час	Відстань
I	74 км/год		7 год	?
II	?, на 8 км/год менше

Розв'язання

1) 74 ‒ 8 = 66 (км/год) ‒ швидкість другого автомобіля

2) 74 + 66 = 140 (км) ‒ на стільки збільшується відстань між автомобілями щогодини.

3) 140 • 7 = 980 (км) ‒ відстань між автомобілями через 7 год.

Відповідь: через 7 год відстань між автомобілями 980 км.

 

Вправа 436 Із міст Конотоп і Сміла одночасно назустріч один одному виїхали велосипедист і легковий автомобіль. Велосипедист їхав зі швидкістю 11 км/год, а автомобіль — у 7 разів швидше. Знайдіть відстань між цими містами, якщо велосипедист і автомобіль зустрілися через 4 год після початку руху.

	Швидкість		Час	Відстань
Велосипедист	11 км/год		4 год	?
Автомобіль	?, у 7 разів більше

Розв'язання

1) 11 • 7 = 77 (км/год) ‒ швидкість легкового автомобіля.

2) 11 + 77 = 88 (км) ‒ на стільки зменшується відстань між велосипедистом і автомобілем.

3) 88 • 4 = 352 (км) ‒ відстань між містами.

Відповідь: відстань між містами 352 км.

 

Вправа 437 Із двох селищ одночасно назустріч один одному вирушили велосипедист і пішохід. Пішохід рухався зі швидкістю 3 км/год, що в 4 рази менше від швидкості велосипедиста. Знайдіть відстань між селищами, якщо велосипедист і пішохід зустрілися через 3 год після початку руху.

	Швидкість		Час	Відстань
Велосипедист	3 км/год		3 год	?
Пішохід	?, у 4 раз більше

Розв'язання

1) 3 • 4 = 12 (км/год) ‒ швидкість велосипедиста.

2) 3 + 12 = 15 (км) ‒ на стільки зменшується відстань між ними щогодини.

3) 15 • 3 = 45 (км) ‒ відстань між селищами.

Відповідь: відстань між селищами 45 км. 

 

Вправа 438 Чи є правильним твердження:

 

Вправа 439 Як зміниться добуток двох натуральних чисел, якщо:

1 ) один із множників збільшити у 8 разів; Добуток збільшиться у 8 разів.

2) один із множників зменшити в 5 разів; Добуток зменшиться у 5 разів.

3) кожний із множників збільшити в 6 разів; 

Добуток збільшиться у 36 разів (6 • 6 = 36)

4) один множник збільшити в 13 разів, а другий — у 40 разів; 

Добуток збільшиться у 520 разів (13 • 40 = 520)

5) один множник збільшити у 12 разів, а другий зменшити в 3 рази? 

Добуток збільшиться у 4 рази (12 : 3 = 4)

 

Вправа 440 Із двох хуторів, відстань між якими дорівнює З км, вийшли одночасно назустріч один одному дві хуторянки. Одна із них рухалася зі швидкістю 5 км/год, а друга — зі швидкістю 4 км/год. Якою буде відстань між хуторянками через 2 год після початку руху?

Розв'язання

1) 5 • 2 = 10 (км) ‒ відстань першої хуторянки.

2) 4 • 2 = 8 (км) ‒ відстань другої хуторянки.

3) 10 + 8 ‒ 3 = 15 (км) ‒ відстань між хуторянками (пішоходи йшли назустріч, тому відстань 3 км повторюється двічі).

Відповідь: через 2 год після початку руху відстань між пішоходами буде 15 км.

  

Вправа 441* Замість зірочок поставте такі цифри, щоб множення було виконано правильно:

х  43    28   344   86    1204

х 52   42  104 208   2184

х 98     9  882

х   66    101     66  66     6666

Вправа 442 Замість зірочок поставте такі цифри, щоб множення було виконано правильно:

х   57     69   513  342    3933

х  74    17   518   74    1258

х 52   11   52 52   572

х 254     32   508 762   8128

Вправа 443  Сума й добуток чотирьох натуральних чисел дорівнюють 8. Що це за числа?

1, 2, 4 (1 + 1 + 2 + 4 = 8 і 1 • 1 • 2 • 4 = 8)

  

Вправа 444 У записі 1 * 2 * 3 * 4 * 5 замініть зірочки на знак ≪+≫ або знак ≪•≫ та поставте дужки так, щоб значення отриманого виразу дорівнювало 100. 1 • (2 + 3) • 4 • 5 = 100 або (1 • 2 + 3) • 4 • 5 = 100

 

 

Завдання 445 У записі 1 * 2 * 3 * 4 замість кожної зірочки можна поставити знак «+» або знак «•». Чому дорівнює найбільше значення виразу, який можна отримати? 1 + 2 • 3 • 4 = 1 + 24 = 25

 

Вправи для повторення

Вправа 446 Знайдіть величину кута АВМ (рис. 148), якщо <MBK — прямий і <ABM = <CBK.

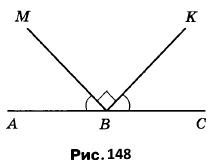
Розв'язання

∠АВС = 180° ‒ розгорнутий кут.

∠МВК = 90° ‒ прямий кут.

∠АВМ + ∠СВК = ∠АВС ‒ ∠МВК = 180° ‒ 90° = 90°

За умовою задачі ∠АВМ = ∠СВК, тому 

2∠АВМ = 90°

∠АВМ = 90° : 2 = 45°

 

Вправа 447 Кут ABC дорівнює 72°, промінь BD — бісектриса кута ABC, промінь BE — бісектриса кута ABD. Обчисліть величину кута СВЕ.

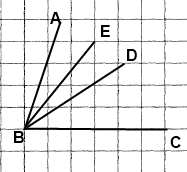
Розв'язання

Промінь BD — бісектриса кута ABC, тому

∠СВD = ∠АВD = ∠АВС : 2 = 72° : 2 = 36°

Промінь BE — бісектриса кута ABD, тому

∠ЕВD = ∠АВD : 2 = 36° : 2 = 18°

∠СВЕ = ∠ЕВD + ∠СВD = 36° + 18° = 54°

 

Вправа 448 За формулою а = b : 4 ‒ 6 знайдіть значення а, якщо:

1) b = 600; 

Якщо b = 600, тоді а = b : 4 ‒ 6 = 600 : 4 ‒ 6 = 150 ‒ 6 = 144

2) b = 64;

Якщо b = 64, тоді а = b : 4 ‒ 6 = 64 : 4 ‒ 6 = 16 ‒ 6 = 10

3) b = 24.

Якщо b = 24, тоді а = b : 4 ‒ 6 = 24 : 4 ‒ 6 = 6 ‒ 6 = 0

 

Вправа 449 Сума довжин першої і другої сторін трикутника дорівнює 33 см, першої і третьої — 39 см, другої і третьої — 42 см. Знайдіть периметр трикутника.

Розв'язання

1) 33 + 39 + 42 = 114 (см) ‒ подвійний периметр трикутника.

2) 114 : 2 = 57 (см) ‒ периметр трикутника.

Відповідь: периметр трикутника 57 см.

 

Задача від Мудрої Сови

Вправа 426 

1) Складіть із 10 сірників три квадрати. 

2) Складіть із 19 сірників шість квадратів.

3) Які чотири сірники треба забрати (рис. 149), щоб залишилося п’ять квадратів?

Розв'язання

------------------------ у підручниках за 2013, 2018 роки ----------------------- 

Вправа 402* До школи завезли апельсини, мандарини та лимони. Апельсинів було 94 кг, що в 7 разів менше, ніж мандаринів, і на 16 кг більше, ніж лимонів. Скільки всього кілограмів фруктів було завезено до школи?

Розв'язання:  94 + 94 • 7 + (94 - 16)

1) 94 • 7 = 658 (кг) ‒ мандаринів завезли.

2) 94 ‒ 16 = 78 (кг) ‒ лимонів завезли.

3) 94 + 658 + 78 = 830 (кг)

Відповідь: до школи завезли всього 830 кг фруктів.

 

Вправа 403* Школі виділили 8000 грн на покупку телевізора, фотоапарата і DVD‒програвача. Фотоапарат коштує 984 грн, що в 4 рази менше, ніж коштує телевізор, і на 1488 грн менше, ніж DVD‒програвач. Чи вистачить виділених грошей на покупку?

Розв'язання

1) 984 • 4 = 3936 (грн) ‒ ціна телевізора.

2) 984 + 1488 = 2472 (грн) ‒ ціна програвача.

3) 984 + 3936 + 2472 = 7392 (грн) ‒ вартість покупки.

4) 8000 > 7392

Відповідь: виділених грошей вистачить на покупку.

 

Вправа 418** Сума і добуток чотирьох натуральних чисел дорівнюють 8.

Що це за числа? 2, 4, 1

 

Вправа 416° 

х  418      46   2508 1672   19228

х    133      908    1064 1197    120764

х  626      480   5008  2504     300480

Вправа 392 

х 304     29  2736  608    8816

х    328       406     1968  1312      133168

х  934      260   5604 1868     242840

Вправа 393°  

1) 704 • 69 + 1424 = 50000			3) (938 ‒ 543) • 34 = 1343
х  704       69   6336  4224    48576		+48576    1424     50000	_938   543     395	х 395     34  1580 1185    13430

Вправа 397° 

1) 693 • 100 = 69300	3) х 540        20     10800	5) х 760       350     380     228        266000
2) 974 • 1000 = 974000	4) 120 • 400 = 48000	6) х  460        1800      368      46           828000

Вправа 398 

1) 214 • 10 = 2140	3) 10 000 • 546 = 5460000	5) х  580        240       232     116         139200
2) 100 • 328 = 32800	4) х 140        80     11200	6) х 270        3000       810000

Завдання 426

На фермі є 78 корів, кожна з яких дає за день 12 л молока. Молоко з ферми вивозять у бідонах ємністю 40 л. Одного дня на фермі був 21 порожній бідон. Чи вистачить бідонів, щоб вивезти з ферми молоко, яке надоїли за цей день?

Розв’язання

1) 12 • 78 = 936 (л) – всього молока дають корови в день.

2) 936 : 40 = 23 (ост. 16)

Відповідь: не вистачить бідонів.

 

Вправа 419 При яких значеннях а є правильною рівність:

1) а • 5 = 5    а = 5 : 5    а = 1	4) а • 1 = 1      а = 1 : 1      а = 1	7) 0 • а = а     а = 0
2) а • 5 = 0      а = 0 : 5     а = 0	5) а • 1 = а    а = 1 або а = 0	8) 0 • а = 0;    а ‒ будь‒яке число
3) а • 5 = а    а = 0	6) а • а = а    а = 0 або а = 1	9) а • 1 = 0    а = 0

Інші завдання дивись тут ...