Завдання 1 Дільники
1) число 6 є дільником числа 24, бо 24 ділиться націло на 6.
2) число 6 не є кратне числу 24, бо 6 не ділиться націло на 24.
3) число 5 не є дільником числа 51, бо 51 не ділиться націло на 5
4) число 9 є дільником числа 99, бо 99 ділиться націло на 9
5) число 18 є кратним числа 3, бо 18 ділиться націло на 3.
6) число 28 не є кратне числу 8, бо 28 не ділиться націло на 8.
Завдання 2
1) дільниками 24 є числа: 2, 3, 4, 6, 8, 12, 24
2) кратними 6 є числа: 6, 12, 18, 30
3) дільниками 20 і 24 є числа: 2, 4
4) дільниками 24 і кратними 4 є числа: 4, 8, 12
Завдання 3
1) найбільший дільник числа 19 735 — це саме число 19 735
2) найменший дільник числа 19 735 - це число 1.
3) найменше кратне числа 19 735 - це саме число 19 735
Завдання 4
1) дільники числа 18: 1, 2, 3, 6, 9, 18
2) дільники числа 8: 1, 2, 4, 8
3) дільники числа 13: 1, 13
4) дільники числа 56: 1, 2, 4, 7, 8, 14, 28, 56
Завдання 5
1) дільники числа 30: 1, 2, 3, 5, 6, 10, 15, 30
2) дільники числа 12: 1, 2, 3, 4, 6, 12
3) дільники числа 23: 1, 23
4) дільники числа 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Завдання 6
Чи можна поділити порівну 28 зошитів між:
1) 4 дітьми; Так, бо 28 ділиться націло на 4.
2) 6 дітьми; Ні, бо 28 не ділиться націло на 6.
3) 7 дітьми; Так, бо 28 ділиться націло на 7.
4) 8 дітьми? Ні, бо 28 не ділиться націло на 8.
Завдання 7
Чи можна розкласти порівну 48 тістечок на:
1) 3 тарілки; Так, бо 48 ділиться націло на 3.
2) 6 тарілок; Так, бо 48 ділиться націло на 6.
3) 9 тарілок? Ні, бо 48 не ділиться націло на 9.
Завдання 8, 9 Кратні числа
|
П'ять чисел кратні числу:
1) 7: 7, 14, 21, 28, 35
2) 30: 30, 60, 90, 120, 150
3) 100: 100, 200, 300, 400, 500
4) 34: 34, 68, 102, 136, 170
|
Чотири числа кратні числу:
1) 16: 16, 32, 48, 64
2) 12: 12, 24, 36, 48
3) 150: 150, 300, 450, 600
4) 47: 47, 94, 141, 188
|
Завдання 10
Із 28, 36, 48, 64, 92, 100, 108, 110 є кратними:
1) 4: 28, 36, 48, 64, 92, 100, 108
2) 6: 28, 64, 92, 100, 110
Завдання 11
1) кожне із чисел а і b ділиться націло на 5; Ні.
Наприклад, якщо а = 2, b = 3, тоді a + b = 2 + 3 = 5, але кожне з чисел 2 і 3 не ділиться на 5.
2) одне із чисел ділиться націло на 5, а друге — ні? Ні.
Наприклад, нехай перший доданок 5, а сума 25, тобто діляться на число 5, тоді
25 – 5 = 20 — другий доданок також ділиться на число 5.
Наприклад, нехай перший доданок 10, а сума 50, тобто діляться на число 5, тоді
50 – 10 = 40 – другий доданок також ділиться на число 5.
Завдання 12 Ознаки подільності чисел
Відомо, що жодне із чисел а і b не ділиться націло на 11. Чи є правильним твердження, що їхня сума також не ділиться націло на 11? Ні, не завжди.
Наприклад, якщо а = 19 i b = 15, що не діляться на 11, то їхня сума a + b = 19 + 15 = 34 також не ділиться на 11.
Наприклад, якщо а = 41 i b = 25, що не діляться на 11, то їхня сума a + b = 41 + 25 = 66 ділиться на 11.
Завдання 13, 14
|
1) дільники 15 і 20: 1 , 5
2) дільники 7 і 21: 1, 7
3) дільники 24 і 36: 1, 2, 3, 4, 6, 12
4) дільники 20 і 21: 1
|
1) дільники 12 і 18: 1, 2, 3, 6
2) дільники 60 і 90: 1, 2, 3, 5, 10, 15, 30
3) дільники 22 і 35: 1
4) дільники 9 і 27: 1, 3, 9
|
Завдання 15, 16
|
1) кратні 3 і 4: 12
2) кратні 6 і 12: 24
3) кратні 4 і 6: 12
|
1) кратні 5 і 9: 45
2) кратні 8 і 32; 32
3) кратні 8 і 12. 24
|
Завдання 17
1) двоцифрові числа, кратні 19: 19, 38, 57, 76, 95
2) трицифрові числа, кратні 105: 105, 210, 315, 420, 525, 630, 735, 840, 945
Завдання 18
Двоцифрові числа, кратні 23: 23, 46, 69, 92
Завдання 19
18 < х < 36 правильна при х, що кратні числу 4: 20, 24, 28, 32
Завдання 20
25 < х < 60 правильна при х, що кратні числу 6: 30, 36, 42, 48, 54
Завдання 21
7 < х < 40 правильна при х, які є дільниками числа 80: 8, 16, 24, 32
Завдання 22
14 < х < 50 правильна при х, які є дільниками числа 98: 49
Завдання 23
Безліч чисел, кратні числам 9 і 11 та більше за 100.
Завдання 24
Числа 36 і 72, кратні числам 9 і 12 та менші від 100. Існує два таких числа.
Завдання 25
1) число а кратне 6, то воно кратне 3; Так, наприклад, число 12.
2) число а кратне 3, то воно кратне 6; Ні, наприклад, число 3.
3) число а кратне числам 3 і 4, то воно кратне 12; Так, наприклад, число 12
4) число а кратне числам 4 і 6, то воно кратне 24? Ні, наприклад, число 12
Завдання 26
При діленні числа а на 7 отримали остачу 4. Яку умову має задовольняти число b, щоб сума а + b була кратною 7?
Оскільки число а ділиться з остачею, тому запишемо його у вигляді: а = 7p + 4.
За умовою a + b = 7n, виразимо змінну b і підставимо у вираз а, одержимо:
b = 7n – a = 7n – (7p + 4) = (7n – 7p) – 4 = (7n – 7p) – (7 – 3) = (7n – 7p – 7) + 3 =
= 7(n – p – 1) + 3, отже, число b при ділення на число 7 повинно мати остачу 3.
Завдання 27
При діленні числа а на 9 отримали остачу 5. Яку умову має задовольняти число щоб різниця а - b була кратною 9?
Оскільки число а ділиться з остачею, тому запишемо його у вигляді: а = 9p + 5
За умовою a – b = 9n, виразимо змінну b і підставимо у вираз а, одержимо:
b = a - 9n = 9p + 5 - 9n = (9p - 9n) + 5 = 9(p - n) + 5, отже, число b при ділення на 9 повинно мати остачу 5.
Завдання 28
1) 15n кратне 3 при n = 1, 2, 3, ...
2) 15n кратне 5 при n = 1, 2, 3, ...
3) 15n кратне 10 при n = 10, 20, 30, 40, ...
4) 15n кратне 11 при n = 11, 22, 33, 44, ...
Завдання 29
1) значення виразу Зn + 2 кратне числу 2, якщо 3n кратне числу 2, тобто при натуральних значеннях n = 2, 4, 6, ..
2) значення виразу 4n + 3 кратне числу З, якщо 4n кратне числу 3, тобто при натуральних значеннях n = 3, 6, 9, ..
Завдання 30
Доведіть, що двоцифрове число, яке записано двома однаковими цифрами, кратне 11.
Подамо двоцифрове число у вигляді: аа = 10а + а = (10 + 1)а = 11а, тому кратне 11.
Завдання 31
Доведіть, що трицифрове число, яке записано трьома однаковими цифрами, кратне 37.
Подамо трицифрове число у вигляді:
ааа = 100а + 10а + а = (100 + 10 + 1)а = 111а = 37 • 3 • а, тому кратне 37.
Завдання 32
До одноцифрового числа дописали одну цифру, у результаті чого воно збільшилося в 41 раз. Яку цифру й до якого числа дописали?
Отримаємо двоцифрове число ab = 41a або ba = 41a, що кратні 41.
Якщо а = 1, тоді 41 • 1 = 41; якщо а = 2, тоді 41 • 2 = 82
Відповідь: до числа 1 ліворуч дописали цифру 4, або до числа 2 ліворуч дописали цифру 8.
Завдання 33
У двоцифровому числі закреслили одну цифру, у результаті чого воно зменшилося в 17 разів. Яку цифру та в якому числі закреслили?
Розкладемо довільне число ab на розрядні доданки, одержимо:
ab = 10a + b
Тоді 17а = 10а + b або 17b = 10a + b.
Підставимо значення а у вираз 17а = 10а + b.
Якщо а = 1, тоді 17 = 10 • 1 + 7, тому b = 7 — одноцифрове число
Якщо а = 2, тоді 34 = 10 • 2 + 14, тому b = 14 — двоцифрове число
Якщо а = 3, тоді 51 = 10 • 3 + 21, тому b = 21 — двоцифрове число
Якщо а = 4, тоді 68 = 10 • 4 + 28, тому b = 28 — двоцифрове число
Якщо а = 5, тоді 85 = 10 • 5 + 35, тому b = 35 — двоцифрове число
Якщо а = 6, тоді 102 — трицифрове число.
Аналогічно підставимо значення b у вираз 17b = 10a + b.
Якщо b = 1, то 17 = 10 • 1 + 1
Якщо b = 2, то 34 = 10 • 3 + 2
Якщо b = 3, то 51 = 10 • 5 + 3
Якщо b = 4, то 68 = 10 • 6 + 4
Якщо b = 5, то 85 = 10 • 8 + 5
Якщо b = 6, то 102 — трицифрове число.
Відповідь: у числі 17 закреслили цифру 7; у числі 85 закреслили цифру 8.
Вправи для повторення
Завдання 34 Вирази
1) 0,2а • 50b = 10ab
Якщо а = 4, b = 3,6, тоді 10ab = 10 • 4 • 3,6 = 144
2) 0,4х • 25у = 10ху
Якщо х = 2,4, у = 3, тоді 10ху = 10 • 2,4 • 3 = 72
Завдання 35 Рівняння
|
1) 2,48х + 3,52х = 1,26
(2,48 + 3,52)х = 1,26
6х = 1,26
х = 1,26 : 6
х = 0,21
|
2) 4,63х + 3,37х = 1,92
(4,63 + 3,37)х = 1,92
8х = 1,92
х = 1,92 : 8
х = 0,24
|
Завдання 36
До їдальні привезли 146 кг овочів: 6 ящиків помідорів і 8 ящиків огірків. Скільки кілограмів огірків у кожному ящику, якщо помідорів у кожному ящику було 7,8 кг, а маси огірків у кожному ящику однакові?
Розв’язання
1) 7,8 • 6 = 46,8 (кг) – помідорів привезли;
2) 146 – 46,8 = 99,2 (кг) – огірків привезли;
3) 99,2 : 8 = 12,4 (кг) – огірків в кожному ящику.
Відповідь: 12,4 кг.
Завдання 37 Ділення з остачею
|
1) 429 : 2 = 214 (ост 1)
2) 5001 : 2 = 2500 (ост 1)
|
3) 768 : 10 = 76 (ост 8)
4) 9123 : 10 = 912 (ост 3)
|
5) 134 : 5 = 26 (ост 4)
6) 2867 : 5 = 573 (ост 2)
|
Завдання 38
1) 83 : 7 = 11 (ост. 6), тому 83 = 7 • 11 + 6
2) 171 : 17 = 10 (ост. 1), тому 171 = 17 • 10 + 1
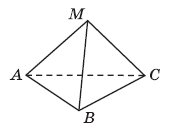
Завдання 39
Задача від Мудрої Сови. Складіть із шести сірників чотири рівносторонніх трикутники зі стороною, яка дорівнює довжині одного сірника.