ГДЗ частина 1 Заїка математика 4 клас завдання 199 – 224 Відповіді до підручника

ДІЛЕННЯ З ОСТАЧЕЮ.

ПЛОЩИННІ ГЕОМЕТРИЧНІ ФІГУРИ

1, 4, 2, 5, 3	1, 4, 2, 5, 3
102 : 2 + 34 • 5 – 130 : 5	730 : 10 – 84 : 4 + 800 : 20

Вправа 200

Числа, які діляться на 2 без остачі (таблиця ділення на число 2):

26, 40, 104, 328, 702, 430.

Числа, які діляться на 5 без остачі (таблиця ділення на число 5): 40, 225, 430

Числа, які діляться на 10 без остачі: 40, 430

Вправа 201 Господарі зібрали з присадибної ділянки 43 кг моркви. На зиму моркву розфасували в ящики, по 5 кг у кожний. Скільки ящиків для цього знадобилося? Чи всі ящики були наповнені дощенту?

Розв’язання

43 : 5 = 8 (ост. 3)

Відповідь: для цього знадобилося 9 ящиків, один ящик не був наповнений дощенту.

Вправа 202 Ділення з остачею

22 : 3 = 6 (ост. 4)

22 кружечки ділили.

Ділили на 3 рівні частини, по 6 кружечків у кожній.

Ще 4 кружечки залишилося.

Вправа 203

24 : 5 = 4 (ост. 4)	74 : 8 = 9 (ост. 2)	99 : 2 = 49 (ост. 1)
4 • 5 + 4 = 24	9 • 8 + 2 = 74	49 • 2 + 1 = 99
25 : 4 = 6 (ост. 1)	74 : 9 = 8 (ост. 2)	99 : 4 = 24 (ост. 3)
6 • 4 + 1 = 25	8 • 9 + 2 = 74	24 • 4 + 3 = 99

Вправа 204

Частку називають неповною, бо наявна остача.

Вправа 205 Урожай груш з домашнього саду розклали в 7 ящиків, по 12 кг у кожний, і ще залишилося 9 кг груш. Скільки кілограмів груш було зібрано?

Короткий запис

Розклали — ?, 7 ящ. по 12 кг

Залишилося — 9 кг

Зібрано — ?

Розв’язання

1) 12 • 7 = 84 (кг) – груш у ящиках.

2) 84 + 9 = 93 (кг)

Відповідь: зібрано 93 кілограми груш.

Вправа 206

Можна поділити на дві групи: прямокутники (перша і остання фігури) і не прямокутники (решта — фігури посередині).

Можна поділити на дві групи: за кольором і без кольору.

Вправа 207

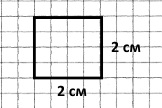
Прямокутник, у якого всі сторони рівні: квадрата зі стороною 2 см.

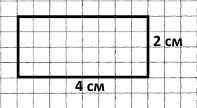
Прямокутник, у якого одна сторона більша за суміжну на 2 см: прямокутник довжиною 4 см і шириною 2 см.

Вправа 208

Чотирикутники три: OPRS, XYZT, AMOR. Прямокутники два: XYZT, AMOR.

Вправа 209 Усі трицифрові числа, які можна скласти, використовуючи такі слова: двісті, сорок, шістдесят, три, п'ять, вісім: 243, 245, 248, 263, 265, 268.

Вправа 210 Протягом трьох днів виставку художніх робіт відвідало 960 осіб. Першого дня було 315 відвідувачів, другого дня на 45 осіб більше, ніж першого. Скільки осіб відвідало виставку третього дня?

Короткий запис

Всього — 960 ос.

I — 325 ос.

II — ?, на 45 ос. більше, ніж I дня.

III — ?

Розв’язання

1) 315 + 45 = 360 (ос.) – відвідувачів другого дня;

2) 315 + 360 = 675 (ос.) – відвідувачів за перших два дні разом;

3) 960 – 675 = 285 (ос.) – відвідувачів третього дня.

Відповідь: третього дня виставку відвідало 285 осіб.

Вправа 211

1) Чотирикутник АВСD є прямокутником.

2) Вершини та прямі кути фігури: А, В, С, D

3) Визначення прямокутника. Прямокутник — чотирикутник, у якого всі кути прямі.

4) Прямокутник має 4 сторони, 4 кути, 4 вершини.

5) Рівні сторони: AB = DC, BC = AD

6) Периметр прямокутника.

ПЕРЕВІР СЕБЕ

Вправа 212 Числа, більші від 150, але менші від 200, які діляться без остачі на 5: 155, 160, 165, 170, 175, 180, 185, 190, 195

Вправа 213

Сума добутків чисел 170 і 3 та 225 і 2: 170 • 3 + 225 • 2 = 510 + 450 = 960

Вправа 214

П'ять однакових наборів фломастерів коштують 300 грн. Скільки коштують 10 таких наборів фломастерів?

Короткий запис

5 н. — 300 грн

10 н. — ?

Розв’язання

1 спосіб

300 : 5 • 10 = 60 • 10 = 600 (грн) – вартість 10 таких наборів.

2 спосіб

300 • (10 : 5) = 300 • 2 = 600 (грн) – вартість 10 таких наборів.

Відповідь: 10 таких наборів коштують 600 гривень.

Вправа 215

За 180 грн купили 6 однакових наборів фломастерів. Скільки таких наборів можна купити за 210 грн?

Короткий запис

6 н. — 180 грн

? н. — 210 грн

Розв’язання

210 : (180 : 6) = 7 (н.) – наборів можна купити.

Відповідь: можна купити 7 таких наборів.

Вправа 216

(a – b : c + d) • k дії: 2, 1, 3, 4 a • b – b • c + c • a дії: 1, 4, 2, 5, 3

Якщо a = 130, b = 120, c = 4, d = 200, k = 2, тоді

(a – b : c + d) • k = (130 – 120 : 4 + 200) • 2 = (130 – 30 + 200) • 2 = 600

Якщо a = 30, b = 20, c = 15, тоді

a • b – b • c + c • a = 30 • 20 – 20 • 15 + 15 • 30 = 600 – 300 + 450 = 750

Вправа 217

Обчислення

Перевірка

+586

275

861

+356

299

655

_646

385

261

_520

325

195

_861

586

275

_861

275

586

_655

299

356

_655

356

229

+261

385

646

_646

261

385

+195

325

520

_520

195

325

Вправа 218

1) Одиниці довжини: 1 мм, 1 см, 1 дм, 1 м

2) Одиниці маси: 1 г, 1 кг, 1 ц, 1 т

3) Одиниці часу: 1 с, 1 хв, 1 год, 1 доба, 1 тиждень, 1 рік

4) Одиниці вартості: 1 к., 1 грн

Вправа 219 Одиниці вимірювання

5 м 40 см = 540 см

5 ц 20 кг = 520 кг

7 дм 3 см = 73 см

2 год 30 хв = 150 хв

342 см = 3 м 42 см

219 кг = 2 ц 19 кг

41 см = 4 дм 1 см

185 хв = 3 год 5 хв

Вправа 220

40 км + 265 км = 305 км

250 кг + 74 кг = 324 км

13 год + 10 год = 23 год

173 м – 56 м = 117 м

346 т – 60 т = 286 т

25 хв – 17 хв = 8 хв

25 км • 2 = 50 км

52 кг • 4 = (50 кг + 2 кг) • 4 = 208 кг

5 год • 6 = 30 год

18 м : 3 = 6 м

24 т : 8 = 3 т

60 хв : 2 = 30 хв

Вправа 221

25 : 6 = 4 (ост. 1)

76 : 5 = 15 (ост. 1)

87 : 4 = 12 (ост. 3)

73 : 10 = 7 (ост. 3)

Вправа 222

а) Усього квадратів можна виділити на кожному рисунку:

На І малюнку 14 (кв.) На ІІ малюнку 30 (кв.)

б) Квадратна дошка розділена на квадрати двох кольорів. Чи можна цю дошку розрізати на прямокутники, що складаються з двох квадратиків різних кольорів? Ні.

Вправа 223 Дії з іменованими числами

2 дм 5 см + 7 дм 2 см = 9 дм 7 см

5 м 45 см + 3 м 55 см = 9 м

40 м • 2 = 80 м 20 см • 2 = 40 см

3 год • 3 = 9 год 10 хв • 3 = 30 хв

10 год 40 хв – 5 год 25 хв = 5 год 15 хв

45 т 2 ц – 13 т = 32 т 2 ц

80 т : 4 = 20 т 8 т 4 ц : 4 = 2 т 1 ц

35 грн : 5 = 7 грн 5 грн 10 коп. : 5 = 1 грн 2 коп.

Вправа 224

а) Полічили сотнями до 1000 в прямому і зворотному напрямках:

100, 200, 300, 400, 500, 600, 700, 800, 900, 1000