© Барна Р., 2019
Серія "Вчимось разом" до підручника "Математика 2 клас Оляницька Л.В."
Завдання 880
Властивості множення: a • b = b • a (переставний закон множення) a • 0 = 0 (множення на нуль)
0 • a = 0 (множення нуля) 1 • a = a (множення одиниці) a • 1 = a (множення на один)
Властивості ділення: a : a = 1 (ділення однакових чисел) 0 : a = 0 (ділення нуля) a : 1 = a (ділення на один)
Завдання 881 Взаємозв'язок множення і ділення
Для рівності на множення можна скласти дві рівності на ділення.
|
8 • 1 = 8 8 : 8 = 1 8 : 1 = 8 |
4 • 10 = 40 40 : 4 = 10 40 : 10 = 4 |
5 • 9 = 45 45 : 5 = 9 45 : 9 = 5 |
6 • 0 = 0 0 : 6 = 0 |
Завдання 882 Рівняння
6 : 6 = 1 (бо 1 • 6 = 6) 80 : 10 = 8 (бо 80 : 8 = 10) 12 • 1 = 12 (бо 12 : 12 = 1)
0 : 4 = 0 (бо 0 • 4 = 0) 2 • 10 = 20 (бо 20 : 10 = 2) 1 • 21 = 21 (бо 21 : 1 = 21)
Завдання 883 Складена задача на знаходження зменшуваного
У коробці лежали олівці. Двоє дітей взяли по 8 олівців, і в коробці залишилося 18 олівців. Скільки олівців було в коробці спочатку?
|
Було |
Взяли |
Залишилось |
|
? |
2 дітей по 8 олівців |
18 олівців |
Короткий запис
Було — ?
Взяли — ? ол., 2 дітей по 8 олівців
Залишилось — 18 олівців
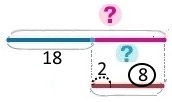
Вираз 18 + 2 • 8
|
Короткий запис №1 Взяли — ? ол., 2 дітей по 8 олівців |
Короткий запис №2 Було — ? Взяли — 16 олівців Залишилось — 18 олівців |
План розв’язування
1) Скільки олівців взяли діти?
2) Скільки олівців було в коробці спочатку?
Розв’язання
1) 8 • 2 = 16 (ол.) – олівців взяли діти.
2) 18 + 16 = 34 (ол.) – олівців було в коробці спочатку.
Відповідь: спочатку в коробці було 34 олівці.
Завдання 884 Непряма проста задача на збільшення у декілька разів
Синові 8 років, і це в 4 рази менше, ніж батькові. Скільки років батькові?
Короткий запис
Син — 8 років, це в 4 рази менше
Батько — ?
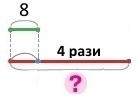
Розв’язання
Якщо синові у 4 рази менше років, то батькові у 4 рази більше, тому
8 • 4 = 32 (р.) – років батькові.
Відповідь: батькові 32 роки.
Завдання 885 Одна сторона прямокутника дорівнює 8 см, інша сторона — на 4 см менша. Накресли цей прямокутник. Знайди його периметр.
8 – 4 = 4 (см) – довжина іншої сторони.
Накреслимо прямокутник довжиною 8 см і шириною 4 см.
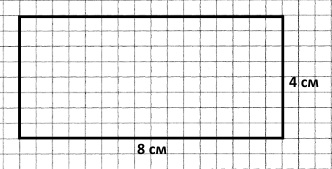
Р = 8 • 2 + 4 • 2 = 16 + 8 = 24 (см) – периметр прямокутника довжиною 8 см і шириною 4 см.
2 спосіб Р = (8 + 4) • 2 = 24 (см) – периметр прямокутника довжиною 8 см і шириною 4 см.
3 спосіб Р = 8 + 4 + 8 + 4 = 24 (см) – периметр прямокутника довжиною 8 см і шириною 4 см.
Завдання 886
|
45 : 9 : 5 = 5 : 5 = 1 3 • 2 • 6 = 6 • 6 = 36 |
8 • 4 • 1 = 32 • 1 = 32 64 : 8 : 2 = 8 : 2 = 4 |
0 : 7 + 48 = 0 + 48 = 48 26 + 5 : 5 = 26 + 1 = 27 |
74 – 10 • 6 = 74 – 60 = 14 7 • 9 – 7 = 7 • 8 = 56 |
Завдання 887 Непряма проста задача на зменшення у декілька разів
Мамі 27 років, і це в 3 рази більше, ніж доньці. Скільки років доньці?
Короткий запис
Мама — 27 років, це в 3 рази більше
Донька — ?
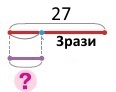
Розв’язування
Якщо мамі у 3 рази більше років, тоді доньці у 3 рази менше, тому
27 : 3 = 9 (р.) – років доньці
Відповідь: доньці 9 років.
Завдання 888 Рівняння
Множник • Множник = Добуток
Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
|
Множник |
1 |
27 : 3 = 9 |
9 |
3 |
6 |
|
Множник |
10 : 1 = 10 |
3 |
0 |
10 |
36 : 6 = 6 |
|
Добуток |
10 |
27 |
9 • 0 = 0 |
3 • 10 = 30 |
36 |
Ділене : Дільник = Частка
Щоб знайти ділене, треба частку помножити на дільник.
Щоб знайти дільник, треба ділене поділити на частку.
|
Ділене |
16 |
7 • 5 = 35 |
63 |
54 • 1 = 54 |
81 |
|
Дільник |
16 : 2 = 8 |
5 |
7 |
1 |
81 : 9 = 9 |
|
Частка |
2 |
7 |
63 : 7 = 9 |
54 |
9 |
Завдання 889
Зменшити 56 на частку чисел 14 і 2: 56 – 14 : 2 = 56 – 7 = 46 + (10 – 7) = 46 + 3 = 49
Додати до числа 25 частку чисел 24 і 3: 25 + 24 : 3 = 25 + 8 = 25 + 5 + 3 = 30 + 3 = 33
Зменшити 64 на добуток чисел 8 і 4: 64 – 8 • 4 = 64 – 32 = 32
Збільшити 31 на частку чисел 21 і 7: 31 + 21 : 7 = 31 + 3 = 34
Завдання 890 Порівняння чисел
Для різницевого порівняння треба від більшого числа відняти менше.
Для кратного порівняння треба більше число поділити на менше.
6 < 24 у 4 рази (бо 24 : 6 = 4) 45 > 5 у 9 разів (бо 45 : 5 = 9)
42 > 6 у 7 разів (бо 42 : 6 = 7) 8 < 64 у 8 разів (бо 64 : 8 = 8)
Завдання 891 Складена задача на різницеве порівняння добутку і числа
7 хлопчиків налили в бочку по 2 відра води кожний. 8 відер використали для поливання квітів. На скільки більше води налили в бочку, ніж використали?
Короткий запис
Налили — ? в., 7 хлопчиків по 2 відра; на ? відра більше
Використали — 8 відер
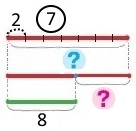
Вираз 2 • 7 – 8
|
Короткий запис №1 Налили — ? в., 7 хлопчиків по 2 відра |
Короткий запис №2 Налили — 14 відер, на ? відра більше Використали — 8 відер |
План розв’язування
1) Скільки відер води налили в бочку?
2) На скільки більше відер води налили в бочку, ніж використали?
Розв’язання
1) 2 • 7 = 14 (в.) – відер води налили в бочку.
2) 14 – 8 = 6 (в.) – на стільки більше відер води налили в бочку, ніж використали.
Відповідь: на 6 відер води більше налили в бочку, ніж використали.
Завдання 892 Обчисли периметр квадрата зі стороною 3 см й прямокутника довжиною 6 см і шириною 3 см. На скільки сантиметрів периметр прямокутника більший за периметр квадрата?
Розв’язання
1) Р = 3 см • 4 = 12 см – периметр квадрата зі стороною 3 см.
2 спосіб Р = 3 см + 3 см + 3 см + 3 см = 12 см – периметр квадрата зі стороною 3 см.
2) Р = 6 см • 2 + 3 см • 2 = 12 см + 6 см = 18 см – периметр прямокутника довжиною 6 см і шириною 3 см.
2 спосіб Р = (6 см + 3 см) • 2 = 9 см • 2 = 18 см – периметр прямокутника довжиною 6 см і шириною 3 см.
3 спосіб Р = 6 см + 3 см + 6 см + 3 см = 18 см – периметр прямокутника довжиною 6 см і шириною 3 см.
3) 18 – 12 = 6 (см) – на стільки сантиметрів периметр прямокутника більший за периметр квадрата.
Відповідь: на 6 сантиметрів більший периметр прямокутника за периметр квадрата.
Завдання 893 Складена задача на знаходження суми добутку і числа
У майстерні пошили 9 дитячих костюмів, використавши по 2 м тканини на кожний костюм. На пошиття костюмів для дорослих пішло 56 м тканини. Скільки метрів тканини використали на пошиття всіх костюмів?
|
Дитячі костюми |
Дорослі костюми |
Всього |
|
9 костюмів по 2 м |
56 м |
? |
Короткий запис
Дитячі — ? м, 9 костюмів по 2 м
Дорослі — 56 м
Всього — ?
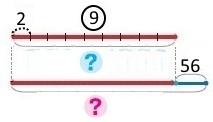
Вираз 9 • 2 + 38
|
Короткий запис №1 Дитячі — ? м, 9 костюмів по 2 м |
Короткий запис №2 Дитячі — 18 м Дорослі — 56 м Всього — ? |
План розв’язування
1) Скільки метрів тканини використали на пошиття костюмів для дорослих?
2) Скільки метрів тканини використали на пошиття всіх костюмів?
Розв’язання
1) 2 • 9 = 18 (м) – метрів тканини використали на пошиття костюмів для дорослих.
2) 18 + 56 = 56 + 4 + 14 = 74 (м) – метрів тканини використали на пошиття всіх костюмів.
Відповідь: для пошиття всіх костюмів використали 74 метри тканини.
Завдання 894
72 : 9 : 4 = 8 : 4 = 2 40 : (2 • 5) = 40 : 10 = 4 100 : 10 + 56 : 7 = 10 + 8 = 18 10 • 2 – 63 : 9 = 20 – 7 = 13
Завдання 895 У шестикутнику довжина кожної сторони дорівнює 2 см. Обчисли периметр многокутника.
Короткий запис
Периметр — ? см, 6 сторін по 2 см
Розв’язання
2 • 6 = 12 (см) – периметр шестикутника.
Відповідь: периметр шестикутника 12 сантиметрів.
Завдання 896 «Магічні» квадрати
|
35 + 27 + 19 = 81 – «магічне» число |
37 + 28 + 19 = 84 – «магічне» число |
||||||
|
25 |
35 |
21 |
1 рядок 81 – 35 – 21 = 25 2 рядок 81 – 23 – 27 = 31 1 стовпець 81 – 25 – 23 = 33 3 рядок 81 – 19 – 33 = 29 |
25 |
40 |
19 |
1 рядок 84 – 25 – 19 = 40 2 рядок 84 – 28 – 34 = 22 2 стовпець 84 – 40 – 28 = 16 3 рядок 84 – 37 – 16 = 31 |
|
23 |
27 |
31 |
22 |
28 |
34 |
||
|
33 |
19 |
29 |
37 |
16 |
31 |
||
Завдання 897 Маса кавуна і дині разом 8 кг, а маса кавуна і двох динь разом 11 кг. Знайди масу одного кавуна й однієї дині.
Міркуємо так.
1) 11 – 8 = 3 (кг) – маса дині.
2) 8 – 3 = 5 (кг) – маса кавуна.
Завдання 898 Які цифри зашифровані буквами?
|
1) А + А + А = ВА Міркуємо так. Сума трьох однакових одноцифрових чисел дає двоцифрове число, значить одноцифрове число більше, ніж 3. Методом підбору умову задовольняє число 5, тобто А = 5. 2 спосіб ВА – А = В0 = А + А, сума двох однакових одноцифрових чисел дає кругле двоцифрове число, А + А = 10, тому А = 5, 5 + 5 + 5 = 15 Відповідь: 5 + 5 + 5 = 15 |
2) СК + С + С = КК Міркуємо так. КК – СК = Х0 = С + С, сума двох однакових одноцифрових чисел дає кругле двоцифрове число 5 + 5 = 10, тобто С = 5. Маємо 5К + 5 + 5 = КК, тоді 50 + 5 + 5 = К0, 60 = К0, К = 6. Відповідь: 56 + 5 + 5 = 66 |
Завдання 899 У кошику лежало 15 червоних і зелених яблук. Червоних яблук було на одне менше, ніж зелених. Скільки червоних і скільки зелених яблук лежало в кошику?
Міркуємо так.
1) 15 – 1 = 14 (яб.) – порівну яблук зелених і червоних.
2) 14 : 2 = 7 (яб.) – червоних яблук.
3) 7 + 1 = 8 (яб.) – зелених яблук.
2 спосіб. Нехай а – червоні яблука, тоді а + 1 – зелені яблука, маємо а + а + 1 = 15, далі а + а = 15 – 1 = 14, 2 • а = 14, а = 14 : 2 = 7 (яб.) – червоних яблук.
а + 1 = 7 + 1 = 8 (яб.) – зелених яблук.
Відповідь: у кошику лежало 7 червоних яблук і 8 зелених.
Завдання 900 У Петра й Олега разом 16 іграшкових автомобілів. Якщо один з друзів віддасть іншому один автомобіль, то в них стане порівну іграшок. Скільки автомобілів у кожного хлопця було спочатку?
Міркуємо так.
1) 16 : 2 = 8 (ав.) – порівну іграшкових автомобілів.
2) якщо один друг віддав іграшки, то спочатку він мав її, тому
8 + 1 = 9 (ав.) – іграшкових автомобілів спочатку було в одного хлопця.
3) якщо другий друг отримав іграшку, то спочатку він не мав її, тому
8 – 1 = 7 (ав.) – іграшкових автомобілів у другого хлопця.
Відповідь: спочатку в одного хлопця було 9 іграшкових автомобілів, у другого – 7 іграшкових автомобілів.
Завдання 901 Будинок має 12 поверхів. Родина Петренків мешкає на дев'ятому поверсі, якщо лічити згори. На якому поверсі мешкає родина Петренків?
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
12 – 9 + 1 = 4 (п.) – поверх, на якому мешкає родина Петренків
Завдання 902 На годинниках 7 год, 7 год 5 хв, 6 год 50 хв. Який із трьох годинників показує правильний час, якщо відомо, що один з годинників поспішає на 5 хв, а ще один відстає на 10 хв?
Міркуємо так. Якщо один з годинників поспішає на 5 хв, то правильний час на 5 хвилин менший, підходить годинник 7 год. Якщо один годинник відстає на 10 хв, то правильний час на 10 хв більший, підходить годинник 7 год.
Відповідь: 7 год
Завдання 903
Чи може сума трьох чисел дорівнювати 2? Може, 0 + 1 + 1 = 2, 0 + 0 + 2 = 2
Чи може різниця двох чисел дорівнювати сумі тих самих чисел? Може, 0 + 0 = 0 – 0, а – 0 = а + 0
На яке число ділиться будь-яке число? На 1, на 0, саме на себе
З дроту зробили трикутник зі сторонами 5, 7 і 9 см. Чи можна утворити з цього відрізка дроту рівносторонній трикутник (трикутник, усі сторони якого рівні)? Можна зі стороною 7 см (5 + 7 + 9) : 3 = 21 : 3 = 7 (см)
Завдання 904 Це найдорожча картина відомого художника Казимира Малевича.
Які фігури ти розпізнаєш на цій картині? Прямокутники, квадрати.
У які групи їх можна об'єднати та за якими ознаками?
Групи за кольором, за формою (прямокутники, квадрати), за розміром (великі, малі).
У якій групі найменша кількість елементів? Найменше квадратів.
Завдання 905 Мама поклала Котигорошку в торбу 14 пиріжків з м'ясом, грибами й капустою. З м'ясом було стільки пиріжків, скільки з капустою, а з грибами на 1 менше, ніж з м'ясом. Скільки було в Котигорошка пиріжків з м'ясом, скільки з капустою, скільки з грибами?
Міркуємо так. Якщо з грибами на 1 менше, ніж з м'ясом, а з м'ясом було стільки пиріжків, скільки з капустою, тоді
1) 14 + 1 = 15 (п.) – пиріжків з м'ясом, грибами й капустою порівно.
2) 15 : 3 = 5 (п.) – пиріжків з з м'ясом або з капустою.
3) 5 – 1 = 4 (п.) – пиріжків з грибами.
Завдання 906 Коли батькові було 28 років, синові виповнилося 5 років. Тепер батькові 35 років. Скільки років синові?
|
1) 35 – 28 = 7 (р.) – років пройшло. 2) 5 + 7 = 12 (р.) – років синові тепер. |
2 спосіб 1) 28 – 5 = 23 (р.) – на стільки років син молодший. 2) 35 – 23 = 12 (р.) – років синові тепер. |
Відповідь: тепер синові 12 років.
Завдання 907 У шухляді лежать 3 пари шкарпеток різного кольору. Скільки шкарпеток потрібно взяти навпомацки, щоб серед них була принаймні пара шкарпеток одного кольору?
Міркуємо так. 1 пара — 2 шкарпетки. Маємо 3 пари шкарпеток різного кольору. Щоб навпомацки точно мати пару шкарпеток одного кольору, треба взяти 4 шкарпетки. Якщо навіть взяти 3 різні шкарпетки, тоді четверта шкарпетка обов’язково утворить пару до одної з них.
Відповідь: 4 шкарпетки.
Завдання 908 Два олівці та гумка коштують стільки ж, скільки один олівець та чотири гумки. У скільки разів олівець дорожчий за гумку?
Міркуємо так. (Ол. + Гум.) + Ол. = (Ол. + Гум.) + Гум. + Гум. + Гум.
Ол. = Гум. + Гум. + Гум. = Гум. • 3
Відповідь: олівець у 3 рази дорожчий за гумку.
Завдання 909
8 чотирикутників: OAKR, OACM, OAPR, NACM, MCPR, NAPR, MCKR, NAKR
Завдання 910 Тетяна, Олена й Микола накреслили по одній фігурі. Тетяна й Микола накреслили фігури з різними периметрами. Олена й Тетяна накреслили фігури з однаковою кількістю сторін. Хто яку фігуру накреслив?
Міркуємо так. Якщо Олена і Тетяна накреслили чотирикутники, наприклад, Олена накреслила квадрат, а Тетяна – прямокутник. А Микола – накреслив не чотирикутник, а трикутник.
Завдання 911 Скільки різних чисел, більших за 10 і менших від 25, можна записати, використовуючи цифри 8; 2; 1; 0?
Міркуємо так. Числа, більші за 10 і менші від 25: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24. Серед них числа з цифрами 8, 2, 1, 0: 11, 12, 18, 20, 21, 22.
2 спосіб
Серед чисел, більших за 10 і менших від 25 та починаються цифрою 1: 11, 12, 18. Аналогічно числа, які починаються цифрою 2: 20, 21, 22.
Відповідь: 6 чисел.
Завдання 912 Логічні ігри
Гра «Судоку». Заповніть вільні клітинки цифрами від 1 до 9 так, щоб в кожному ряду та в кожному стовпчику малого й великого квадратів кожна цифра траплялася тільки один раз.