Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
Домашня самостійна робота №1 (§§ 1-6)
Завдання 1 Точка належить і прямій а, і прямій b.
Точка М перетину прямих a і b належить двом прямим.
A. K Б. L В. M Г. N
Завдання 2 Кут є тупим.
Має градусну міру більше 90°, але меншу 180°.
A. ∠M = 129° Б. ∠T = 90° В. ∠N = 180° Г. ∠L = 78°
Завдання 3 Пара суміжних кутів може дорівнювати...
Сума суміжних кутів дорівнює 180°.
18° + 172° = 190° ≠ 180°
27° + 153° = 180°
A. 18° і 172° Б. 27° і 153° В. 25° і 145° Г. 47° і 134°
Завдання 4 Промінь OP проходить між сторонами кута AOB. Знайдіть градусну міру кута AOB, якщо ∠AOP = 20°, ∠POB = 50°.
За основною властивістю вимірювання кутів ∠AOB = ∠AOP + ∠POB = 20° + 50° = 70°
A. 30° Б. 70° В. 110° Г. неможливо визначити
Завдання 5 Точка L належить відрізку AB. Знайдіть AL, якщо LB = 5 см, AB = 8 см.
За основною властивістю вимірювання відрізків AB = AL + LB
AL = AB – LB = 8 см – 5 см = 3 см
A. 13 см Б. 9 см В. 4 см Г. 3 см
Завдання 6 Один з кутів, що утворилися при перетині двох прямих, дорівнює 160°. Знайдіть кут між прямими.
Кут між прямими менший за 90°, а вертикальні кути різної пари утворюють суміжний кут, тому знайдемо менший вертикальний кут 180° – 160° = 20°.
A. 160° Б. 100° В. 80° Г. 20°
Завдання 7 Відомо, що AB = 4 см, BC = 7 см, AC = 3 см. Укажіть взаємне розміщення точок A, B і C.
Якщо найбільша відстань дорівнює сумі двох інших, тоді точки лежать на одній прямій: 7 см = 4 см + 3 см. Точки відрізка ВС найбільшої довжини будуть крайніми, тому точка А лежить між В і С.
A. точка А лежить між точками В і С
Б. точка В лежить між точками А і С
B. точка С лежить між точками В і А
Г. жодна з точок не лежить між двома іншими
Завдання 8 Промінь OK є бісектрисою кута COB, ∠COB = 70°. Знайдіть ∠AOK.
За основною властивістю вимірювання кутів ∠СОВ = ∠COK + ∠KOB.
Бісектриса кута ділить його на рівні кути ∠COK = ∠KOB.
∠COB = 2∠KOB
∠KOB = ∠COB : 2 = 70° : 2 = 35°
Кут АОВ розгорнутий, ∠АОВ = 180°
За основною властивістю кутів ∠АОВ = ∠АОК + ∠КОВ
∠АОК = 180° – 35° = 145°
A. 110° Б. 135°
B. 145° Г. 155°
Завдання 9 Один із суміжних кутів удвічі менший від другого. Знайдіть більший із цих кутів.
Сума суміжних кутів дорівнює 180°.
180 : 3 = 60 (°) – градусна міра припадає на 1 частину.
60 • 2 = 120 (°) – більший із кутів.
A. 60° Б. 80°
B. 100° Г. 120°
Завдання 10 На площині позначено п'ять точок так, що жодні три з них не лежать на одній прямій. Скільки різних прямих, кожна з яких проходить через деякі дві з даних точок, можна провести?
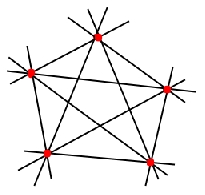
A. 5 Б. 8
B. 10 Г. 15
Завдання 11 Розгорнутий кут ∠MON поділено променями OA і OB на три кути. ∠MOA = 120°, ∠NOB = 110°. Знайдіть градусну міру кута AOB.
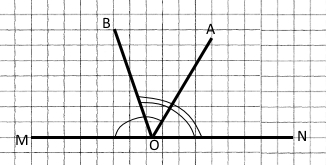
∠MON = ∠MOB + ∠BON,
тоді ∠MOB = ∠MON – ∠BON = ∠MON – ∠NOB = 180° – 110° = 70°.
∠MOA = ∠MOB + ∠BOA = ∠MOB + ∠AOB,
тоді ∠AOB = ∠MOA – ∠MOB = 120° – 70° = 50°.
A. 50° Б. 60°
B. 70° Г. 80°
Завдання 12 Дано два кути, градусні міри яких відносяться як 1 : 2. Різниця кутів, суміжних з ними, дорівнює 70°. Знайдіть більший з даних кутів.
Суміжні кути утворюють розгорнутий кут і їхня сума дорівнює 180°.
Нехай х (°) – менший кут, тоді 180 – х (°) – суміжний із ним, а 2х (°) – більший кут, тоді 180 – 2х (°) – суміжний із ним. Складемо рівняння.
180 – х – (180 – 2х) = 70
180 – х – 180 + 2х = 70
х = 70 (°) – менший кут.
2х = 70 • 2 = 140 (°) – більший кут.
A. 70° Б. 90°
B. 110° Г. 140°
Завдання 13 На відрізку AB завдовжки 74 см позначено точки M і N. Довжини відрізків AM і MN відносяться як 3 : 2, а відрізок NB на 4 см довший за відрізок MN.
Нехай х (см) – довжина одної частини, тоді 3х (см) – відрізок АМ, 2х (см) – відрізок MN, 2х + 4 (см) – довжина MN. За основною властивістю вимірювання відрізків АВ = AM + MN + NB. Складемо рівняння.
3х + 2х + 2х + 4 = 74
7х + 4 = 74
7х = 74 – 4
7х = 70
х = 70 : 7
х = 10
3х = 10 • 3 = 30 (см) – довжина відрізка АМ.
2х = 10 • 2 = 20 (см) – довжина відрізка MN.
2х + 4 = 2 • 10 + 4 = 24 (см) – довжина відрізка MN.
Відповідність між відрізками та їхніми довжинами.
1. AM —> Г. 30 см
2. MN —> А. 20 см
3. NB —> Б. 24 см
Завдання для перевірки знань до §§ 1-6
Завдання 1
Точки, що належать прямій а: B c a, D c a.
Точки, що не належать прямій а: M¢ a, C¢ a.
Завдання 2 Який з даних кутів гострий, тупий, прямий, розгорнутий:
1) А = 92° – тупий кут 2) В = 180° – розгорнутий кут
3) С = 90° – прямий кут 4) D = 31° – гострий кут
Завдання 3 Прямі BN і DK перетинаються в точці A, вони утворюють дві пари вертикальних кутів.
Пари вертикальних кутів: BAD і KAN, BAK і DAN.
Завдання 4 Точка C належить відрізку MN. Знайдіть довжину відрізка CM, якщо MN = 7,2 см, CN = 3,4 см.
За основною властивістю вимірювання відрізків MN = MC + CN, тоді
MC = CM = MN– CN= 7,2 см – 3,4 см = 3,8 см
Відповідь: СМ = 3,8 см.
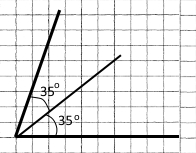
Завдання 5 За допомогою транспортира накресліть кут, градусна міра якого дорівнює 70° та проведіть його бісектрису.
Завдання 6 Прямі AB і CD перетинаються в точці O, ∠AOC = 132°. Знайдіть кут між прямими AB і CD.
Прямі, які перетинаються в одній точці, утворюють дві пари вертикальних кутів.
Кут між прямими не може перевищувати 90°, тобто дорівнює величині меншого із вертикальних кутів.
Вертикальні кути різних пар суміжні, тобто утворюють розгорнутий кут, тому
180° – 132° = 48° – інший вертикальний кут, який є кутом між прямими.
Відповідь: кут між прямими дорівнює 48°.
Завдання 7 Точки М і N належать відрізку AB, довжина якого дорівнює 30 см. Знайдіть довжину відрізка MN, якщо AM = 20 см, BN = 16 см.

Для точки М, яка належить відрізку АВ справедлива основна властивість вимірювання відрізків АВ = АМ + МВ. Тоді МВ = АВ – АМ = 30 см – 20 см = 10 см.
Для точки M, яка належить відрізку NBсправедлива основна властивість вимірювання відрізків BN = BM + MN. Тоді MN = BN – BM = BN– MB= 16 см – 10 см = 6 см.
Відповідь: MN = 6 см.
Завдання 8 Знайдіть суміжні кути, якщо один з них на 12° менший від другого.
Суміжні кути утворюють розгорнутий кут, тому сума їхніх величин дорівнює 180.
Нехай х (°) – один кут, тоді х + 12 (°) – другий кут. Складемо рівняння.
х + х + 12 = 180
2х + 12 = 180
2х = 180 – 12
2х = 168
х = 168 : 2
х = 84 (°) – один кут.
х + 12 = 84 + 12 = 96 (°) другий кут.
Відповідь: кути 84° і 96°.
Завдання 9 Точки A, B і K лежать на одній прямій. Знайдіть довжину відрізка AB, якщо AK = 9,3 см, KB = 3,7 см. Скільки розв'язків має задача?
Задача має 2 розв’язки.
І випадок. Точка В знаходиться між точками А і К. Справедлива основна властивість вимірювання відрізків АК = АВ + ВК, тоді АВ = АК – ВК = АК – КВ = 9,3 см – 3,7 см = 5,6 см.
ІІ випадок. Точка К знаходиться між точками А і В. Справедлива основна властивість вимірювання відрізків АВ = АК + КВ = 9,3 см + 3,7 см = 13 см.
Відповідь: АВ = 5,6 см та АВ = 13 см.
Завдання 10 Який кут утворює бісектриса кута 48° з променем, що є доповняльним до однієї з його сторін?
Бісектриса кута ділить його на рівні кути, 48° : 2 = 24° – кут між бісектрисою і стороною даного кута.
Доповняльний промінь до сторони кута утворює з цим кутом розгорнутий кут, він дорівнює 180.
180° – 48° = 132° – суміжний кут, який утворив доповняльний промінь.
132° + 24° = 156° – шуканий кут.
Відповідь: кут 156°.
Завдання 11 Два кути відносяться як 1 : 3, а суміжні з ними - як 7 : 3. Знайдіть дані кути.
Нехай х (°) – один кут, тоді 180 – х (°) – суміжний до нього кут, а 3х (°) – другий кут, тоді 180 – 3х (°) – суміжний до нього кут. Більшому куту відповідає менший суміжний кут. Складемо рівняння.
(180 – х) : (180 – 3х) = 7/3
3 (180 – х) = 7 (180 – 3х)
3 • 180 – 3х = 7 • 180 – 21х
21х – 3х = 7 • 180 – 3 • 180
18х = 4 • 180
18х = 720
х = 720 : 18
х = 720 : 9 : 2
х = 40 (°) – один кут.
3х = 40 • 3 = 120 (°) – другий кут.
Відповідь: кути 40° і 120°.