Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
Домашня самостійна робота № 2 (§§ 7-10)
Завдання 1 Перпендикулярні прямі
На малюнку 10.20 зображено прямі, що перетинаються.
На малюнку 10.21 зображено паралельні прямі (не перетинаються).
На малюнку 10.22 зображено прямі, що перетинаються.
На малюнку 10.23 зображено перпендикулярні прямі (перетинаються під прямим кутом).
А. мал. 10.20 Б. мал. 10.21 В. мал. 10.22 Г. мал. 10.23
Завдання 2 Паралельні прямі
На малюнку 10.20 зображено прямі, що перетинаються.
На малюнку 10.21 зображено паралельні прямі (не перетинаються).
На малюнку 10.22 зображено прямі, що перетинаються.
На малюнку 10.23 зображено перпендикулярні прямі (перетинаються під прямим кутом).
А. мал. 10.20 Б. мал. 10.21 В. мал. 10.22 Г. мал. 10.23
Завдання 3 Кути 1 і 2 – внутрішні різносторонні на малюнку 10.24.
Кути 1 і 2, які утворені перетином двох прямих січною, – внутрішні різносторонні (між прямими по різні сторони січної).
A. внутрішні односторонні
Б. відповідні
B. вертикальні
Г. внутрішні різносторонні
Завдання 4 Правильне твердження.
Перпендикулярні прямі перетинаються під прямим кутом. Вони завжди мають спільну точку, бо перетинаються.
A. перпендикулярні відрізки завжди мають спільну точку
Б. перпендикулярні прямі завжди мають спільну точку
B. перпендикулярні промені завжди мають спільну точку
Г. перпендикулярні промінь і відрізок завжди мають спільну точку
Завдання 5
На малюнку 10.25 сума внутрішніх односторонніх кутів 61° + 119° = 180°, тому прямі паралельні.
На малюнку 10.26 відповідні кути не є рівними, тому прямі не є паралельними.
На малюнку 10.27 внутрішні різносторонні кути не є рівними, тому прямі не є паралельними.
На малюнку 10.28 сума внутрішніх односторонніх кутів 89° + 89° = 178° < 180°, тому прямі не є паралельними.
А. мал. 10.25 Б. мал. 10.26 В. мал. 10.27 Г. мал. 10.28
Завдання 6 Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 35°. Якою може бути градусна міра одного з інших семи кутів?
При перетині двох паралельних прямих січною утворюється вісім кутів, по чотири з них однакові. Сума внутрішніх односторонніх кутів дорівнює 180°, тому 180° – 35° = 145°
A. 50° Б. 105° B. 145° Г. 55°
Завдання 7 Прямі AB, CD і MN перетинаються в точці O, причому AB ⊥ CD. ∠MOD = 20°. Знайдіть градусну міру кута AON.
Між прямими AB ⊥ CD кут ∠AOC = 90°.
За основною властивістю вимірювання кутів ∠AON = ∠AOC + ∠CON.
Вертикальні кути ∠MOD = ∠CON = 20°.
∠AON = ∠AOC + ∠CON = 90° + 20° = 110°.
А. 20° Б. 70°
B. 110° Г. 160°
Завдання 8 На малюнку 10.29 ∠2 + ∠3 = 175°. Знайдіть ∠1 + ∠4.
При перетині двох прямих утворюються суміжні кути, тому 1 і 2, 3 і 4 – суміжні.
∠1 + ∠4 = (180° – ∠2) + (180° – ∠3) = 360° – ∠2 – ∠3 = 360° – (∠2 + ∠3) = 360° – 175° = 185°.
A. 195°
Б. 185°
B. 175°
Г. 165°
Завдання 9 За малюнком 10.30 знайдіть градусну міру кута x.
При перетині прямих січною зліва відповідні кути рівні 70°, тому прямі паралельні. Для паралельних прямих і січної справа сума внутрішніх односторонніх кутів ∠х + 100° = 180°, звідси ∠х = 180° – 100° = 80°.
А. 80° Б. 70° В. 100° Г. 110°
Завдання 10 На малюнку 10.31 точки A, O і B лежать на одній прямій, ∠AOC = ∠BOD, ∠COK = ∠DOK. Знайдіть, якщо це можливо, градусну міру кута AOK.
Точки A, O і B лежать на одній прямій, тоді AOВ – розгорнутий кут, ∠АОВ = 180°.
∠AOB = ∠AOC + ∠COK + ∠DOK + ∠BOD = 2∠AOC + 2∠COK
∠AOB = 2 (∠AOC + ∠COK)
∠AOK = ∠AOC + ∠COK = ∠AOB : 2 = 180° : 2 = 90°.
А. знайти неможливо Б. 80° В. 90° Г. 100°
Завдання 11 Прямі AB і CD паралельні. Знайти ∠BPD.
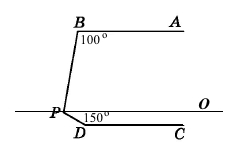
Проведемо пряму PO, паралельну прямій СD. Оскільки PO || CD і AB || CD, тоді за властивістю паралельних прямих PO || AB.
Для паралельних прямих AB і PO та січної РВ внутрішній односторонній кут
∠ВРО = 180° – ∠РВА = 180° – 100° = 80°.
Для паралельних прямих РО і CD та січної РD внутрішній односторонній кут
∠OPD = 180° – ∠PDC = 180° – 150° = 30°.
За основною властивістю вимірювання кутів ∠BPD = ∠BPO + ∠OPD = 80° + 30° = 110°.
А. 100° Б. 110° В. 130° Г. 150°
Завдання 12 Промінь OC проходить між сторонами кута AOB. OK – бісектриса кута AOC, OL – бісектриса кута COB. OK ⊥ OL. Визначте вид кута AOB.
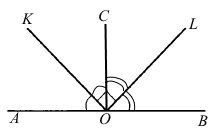
OK – бісектриса кута AOC ділить його пополам, ∠AOC = 2∠KOC.
OL – бісектриса кута COB, ділить його пополам, ∠COB = 2∠COL.
Промінь OC проходить між сторонами кута KOL, тоді за основною властивістю вимірювання кутів ∠KOL = ∠KOC + ∠COL.
Для перпендикулярних бісектрис OK ⊥ OL кут між прямими, на яких вони лежать, ∠KOL = 90°.
Промінь OC проходить між сторонами кута AOB, тоді за основною властивістю вимірювання кутів ∠AOB = ∠AOC + ∠COB, тоді
∠АОВ = 2∠KOC + 2∠COL = 2 (∠KOC + ∠COL) = 2∠KOL = 2 • 90° = 180° – маємо розгорнутий кут.
А. гострий Б. тупий В. прямий Г. розгорнутий
Завдання 13 На кожному малюнку прямі a і b – паралельні, c – січна. Знайти кут між прямими а і с.
1) Для паралельних прямих a і b та січної с відповідні кути рівні, тому між прямими а і с маємо один вертикальний кут 100°. Кут між прямими не перевищує 90°, тому 180° – 100° = 80° – шуканий кут між прямими а і с.
1 — В. 80°
2) Для паралельних прямих a і b та січної с відповідні кути рівні, тому між прямими а і с маємо один вертикальний кут 120°. Кут між прямими не перевищує 90°.
Оскільки для паралельних прямих a і b та січної с сума внутрішніх односторонніх кутів дорівнює 180°, маємо 180° – 120° = 60° – шуканий кут між прямими а і с.
2 — А. 60°
3) Для паралельних прямих a і b та січної с відповідні кути рівні, тому між прямими а і с маємо один з вертикальних кутів 70°. Кут між прямими не перевищує 90°, тому кут 70° – шуканий кут між прямими а і с.
3 — Б. 70°
Завдання для перевірки знань до §§ 7-10
Завдання 1
На малюнку 10.34 зображено паралельні прямі (не перетинаються).
На малюнку 10.32 зображено перпендикулярні прямі (перетинаються під прямим кутом).
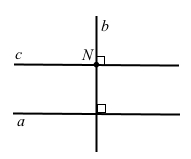
Завдання 2 Побудова перпендикулярних прямих
Накресліть пряму a та позначте точку N, яка їй не належить. За допомогою косинця і лінійки через точку N проведіть:
1) пряму b, перпендикулярну до прямої a;
2) пряму c, перпендикулярну до прямої b.
Дві прямі, перпендикулярні до третьої прямої, паралельні, якщо a ⊥ b і c ⊥ b, тоді a || b.
Завдання 3 Малюнок 10.35
Пари кутів, які утворені двома прямими та січною:
1) 1 і 2 — внутрішні різносторонні кути (між прямими по різні сторони січної);
2) 1 і 3 — внутрішні односторонні кути (між прямими по одну сторону січної);
3) 1 і 4 — відповідні кути (по одну сторону прямих та одну сторону січної).
Завдання 4 Малюнок 10.36
1) Прямі AB, KL і MN перетинаються в точці O. Чи перпендикулярні прямі KL і MN, якщо ∠KOA = 70°, ∠AOM = 19°?
Перпендикулярні прямі перетинаються під прямим кутом, тоді усі утворені кути прямі.
За основною властивістю вимірювання кутів ∠КОМ = ∠КОА + ∠АОМ = 70° + 19° = 89° < 90°. Отже, прямі KL і MN не є перпендикулярними.
Відповідь: ні.
2) Прямі AB, KL і MN перетинаються в точці O. Чи перпендикулярні прямі KL і MN, якщо ∠NOB = 21°, ∠KOB = 111°?
Перпендикулярні прямі перетинаються під прямим кутом, тоді усі утворені кути прямі.
За основною властивістю вимірювання кутів ∠KOB = ∠KON + ∠NOB.
Звідси ∠KON = ∠KOB – ∠NOB = 111° – 21° = 90°. Отже, прямі KL і MN перпендикулярні (KL ⊥ MN).
Відповідь: так.
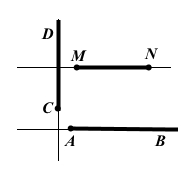
Завдання 5 Накресліть промені AB і CD та відрізок MN так, щоб промінь AB був паралельний відрізку MN і перпендикулярний до променя CD.
Щоб промінь AB був паралельний відрізку MN, вони повинні лежати на паралельних прямих. Щоб промінь AB був перпендикулярний до променя CD, вони повинні лежати на перпендикулярних прямих.
Для простоти спочатку можна намалювати паралельні прямі з перпендикулярною січною, а потім наносити фігури.
Завдання 6 Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 78°. Знайдіть градусні міри решти семи кутів.
При перетині двох паралельних прямих січною утворюється вісім кутів, з яких по чотири рівні.
Якщо один із внутрішніх рівносторонніх кутів дорівнює 78°, тоді інший дорівнює 180° – 78° = 102°.
Відповідь: 78°, 78°, 78°, 102°, 102°, 102°, 102°.
Завдання 7 Малюнок 10.37
Прямі AB, CD і KL перетинаються в точці O, причому AB ⊥ CD. Знайдіть ∠AOK, якщо ∠DOL = 38°.
Прямі AB ⊥ CD, тоді всі утворені ними кути прямі, зокрема ∠АОС = 90°.
За основною властивістю вимірювання кутів ∠АОС = ∠АОК + ∠КОС, звідси
∠АОК = ∠АОС – ∠КОС.
Між прямими KL і CD, що перетинаються, маємо вертикальні кути ∠KOC = ∠DOL.
∠АОК = ∠АОС – ∠КОС = ∠AOC – ∠DOL = 90° – 38° = 52°.
Відповідь: ∠АОК = 52°.
Завдання 8 За малюнком 10.38 знайдіть градусну міру кута x.
Сума внутрішніх односторонніх кутів для двох прямих і нижньої січної 140° + 40° = 180°, значить ці прямі паралельні.
Кут х є вертикальним до внутрішнього одностороннього кута у парі з кутом 130° між паралельними прямими і верхньою січною, тому він дорівнює 180° – 130° = 50°.
Відповідь: ∠х = 50°.
Завдання 9 Прямі AB || CD. Знайдіть ∠BKD.
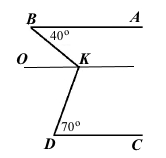
Проведемо пряму OK, паралельну прямій СD. Оскільки OK || CD і AB || CD, тоді за властивістю паралельних прямих OK || AB.
Для паралельних прямих СD і OK та січної DK внутрішні різносторонні кути ∠KDC = ∠OKD = 70°.
Для паралельних прямих OK і АB та січної BK внутрішні різносторонні кути ∠ABK = ∠BKO = 40°.
За основною властивістю вимірювання кутів ∠BKD = ∠BKO + ∠OKD = 70° + 40° = 110°.
Відповідь: ∠BKD = 110°.
Вправа 10 Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо один з них у 4 рази більший за другий.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180.
Нехай х (°) – менший внутрішній односторонній кут, тоді 4х (°) – більший внутрішній односторонній кут. Складемо рівняння.
х + 4х = 180
5х = 180
х = 180 : 5 = (150 + 30) : 5 = 36 (°) – менший внутрішній односторонній кут.
4х = 36 • 4 = (30 + 6) • 4 = 144 (°) – більший внутрішній односторонній кут.
Відповідь: 36° і 144°.
Завдання 11 Пряма m є січною для прямих c і d. Чотири з восьми кутів, що утворилися, дорівнюють по 50°, а решта – по 130°. Чи можна стверджувати, що прямі c і d між собою паралельні?
Якщо нема виконання ознак або властивостей паралельних прямих, тоді не можна стверджувати, що прямі c і d між собою паралельні.
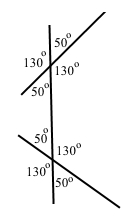
Відповідь: ні.