Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§20 Нерівність трикутника
Завдання 526
1) Чи існує трикутник зі сторонами 1 см, 2 см і 4 см?
Перевіримо нерівність трикутника для найбільшої сторони 4 см > 1 см + 2 см. Не виконується нерівність трикутника.
Відповідь: не існує.
2) Чи існує трикутник зі сторонами 7 дм, 6 дм і 5 дм?
Перевіримо нерівність трикутника для найбільшої сторони 7 дм < 6 дм + 5 дм. Виконується нерівність трикутника.
Відповідь: існує.
3) Чи існує трикутник зі сторонами 3 см, 4 см і 7 см?
Перевіримо нерівність трикутника для найбільшої сторони 7 см = 3 см + 4 см. Не виконується нерівність трикутника.
Відповідь: не існує.
Завдання 527
1) Чи існує трикутник зі сторонами 2 дм, 5 дм і 7 дм?
Перевіримо нерівність трикутника для найбільшої сторони 7 дм = 2 дм + 5 дм. Не виконується нерівність трикутника.
Відповідь: не існує.
2) Чи існує трикутник зі сторонами 2 см, 3 см і 6 см?
Перевіримо нерівність трикутника для найбільшої сторони 6 см > 2 см + 3 см. Не виконується нерівність трикутника.
Відповідь: не існує.
3) Чи існує трикутник зі сторонами 5 дм, 2 дм і 4 дм?
Перевіримо нерівність трикутника для найбільшої сторони 5 дм < 2 дм + 4 дм. Виконується нерівність трикутника.
Відповідь: існує.
Завдання 528
Дві сторони трикутника дорівнюють 2,8 см і 8,4 см. Якому найбільшому цілому числу сантиметрів може дорівнювати третя сторона?
Складемо нерівність трикутника для невідомої сторони а.
8,4 – 2,8 < а < 8,4 + 2,8
5,6 < а < 11,2
Найбільше ціле число, що задовольняє нерівність – 11.
Відповідь: 11 см.
Завдання 529
Дві сторони трикутника дорівнюють 2,7 см і 4,3 см. Якому найменшому цілому числу сантиметрів може дорівнювати третя сторона?
Складемо нерівність трикутника для невідомої сторони а.
4,3 – 2,7 < а < 4,3 + 2,7
1,6 < а < 7
Найменше ціле число, що задовольняє нерівність – 2.
Відповідь: 2 см.
Завдання 530
1) Чи можуть сторони трикутника бути пропорційними числам 2, 3, 4?
Сторони такого трикутника дорівнюють 2х, 3х, 4х. Перевіримо нерівність трикутника для найбільшої сторони 4х < 2х + 3х. Вона виконується, тому трикутник з такими сторонами існує.
2) Чи можуть сторони трикутника бути пропорційними числам 7, 8, 15?
Сторони такого трикутника дорівнюють 7х, 8х, 15х. Перевіримо нерівність трикутника для найбільшої сторони 15х = 7х + 8х. Вона не виконується, тому трикутник з такими сторонами не існує.
3) Чи можуть сторони трикутника бути пропорційними числам 5, 3, 7?
Сторони такого трикутника дорівнюють 5х, 3х, 7х. Перевіримо нерівність трикутника для найбільшої сторони 7х < 5х + 3х. Вона справджується, тому трикутник з такими сторонами існує.
Завдання 531
1) Чи можуть сторони трикутника бути пропорційними числам 5, 1, 4?
Сторони такого трикутника дорівнюють 5х, 1х, 4х. Перевіримо нерівність трикутника для найбільшої сторони 5х = 1х + 4х. Вона не виконується, тому трикутник з такими сторонами не існує.
2) Чи можуть сторони трикутника бути пропорційними числам 5, 6, 7?
Сторони такого трикутника дорівнюють 5х, 6х, 7х. Перевіримо нерівність трикутника для найбільшої сторони 7х < 5х + 6х. Вона виконується, тому трикутник з такими сторонами існує.
3) Чи можуть сторони трикутника бути пропорційними числам 8, 2, 11?
Сторони такого трикутника дорівнюють 8х, 2х, 11х. Перевіримо нерівність трикутника для найбільшої сторони 11х > 8х + 2х. Вона не виконується, тому трикутник з такими сторонами не існує.
Завдання 532
Периметр рівнобедреного трикутника дорівнює 12 см. Чи може бічна сторона цього трикутника дорівнювати 3 см?
У рівнобедреному трикутнику дві сторони рівні, тому
12 – 3 – 3 = 6 (см) – основа трикутника.
Перевіримо нерівність трикутника для найбільшої сторони 6 = 3 + 3. Вона не виконується.
Відповідь: не може.
Завдання 533
Дві сторони рівнобедреного трикутника дорівнюють 5 см і 11 см. Знайдіть периметр цього трикутника.
Нехай бічні сторони дорівнюють по 5 см. Перевіримо нерівність трикутника для найбільшої сторони 11 см > 5 см + 5 см. Вона не виконується, тому такого трикутника не існує.
Нехай бічні сторони дорівнюють по 11 см. Перевіримо нерівність трикутника для більшої сторони 11 см > 11 см + 5 см. Вона виконується, тому шукаємо периметр рівнобедреного трикутника.
Р = 11 • 2 + 5 = 27 (см)
Відповідь: 27 см.
Завдання 534
Дві сторони трикутника дорівнюють 2,5 см і 1,2 см. Яким може бути периметр трикутника, якщо довжина третьої сторони дорівнює цілому числу сантиметрів?
Складемо нерівність трикутника для невідомої сторони а.
2,5 – 1,2 < а < 2,5 + 1,2
1,3 < а < 3,7
Цілі числа, що задовольняють нерівність – 2 і 3.
Для а1 = 2 периметр Р1 = 2,5 + 1,2 + 2 = 5,7 (см)
Для а2 = 3 периметр Р2 = 2,5 + 1,2 + 2 = 6,7 (см)
Відповідь: 5,7 см або 6,7.
Завдання 535
1) Периметр трикутника дорівнює 30 см. Чи може одна з його сторін дорівнювати 14 см?
30 – 14 = 16 (см) – сума двох інших сторін. Виконується нерівність трикутника 14 см < 16 см.
Проте, наприклад, для сторін 15 см і 1 см не виконується нерівність трикутника, бо 15 см = 1 см + 14 см.
Відповідь: може, проте не завжди.
2) Периметр трикутника дорівнює 30 см. Чи може одна з його сторін дорівнювати 15 см?
30 – 15 = 15 (см) – сума двох інших сторін. Не виконується нерівність трикутника.
Відповідь: не може.
3) Периметр трикутника дорівнює 30 см. Чи може одна з його сторін дорівнювати 16 см?
30 см – 16 см = 14 (см) – сума двох інших сторін. Найбільша сторона 16 см, для неї виконується рівність трикутника 16 см < 14 см.
Відповідь: може.
Завдання 536
1) Периметр трикутника дорівнює 40 дм. Чи може одна з його сторін дорівнювати 21 дм?
40 – 21 = 19 (дм) – сума двох інших сторін. Не виконується нерівність трикутника, оскільки 21 см > 19 см.
Відповідь: не може.
2) Периметр трикутника дорівнює 40 дм. Чи може одна з його сторін дорівнювати 20 дм?
40 – 20 = 20 (дм) – сума двох інших сторін. Не виконується нерівність трикутника.
Відповідь: не може.
3) Периметр трикутника дорівнює 40 дм. Чи може одна з його сторін дорівнювати 19 дм?
40 см – 19 см = 21 (см) – сума двох інших сторін. Виконується нерівність трикутника 19 см < 21 см.
Проте, наприклад, для сторін 20 см і 1 см не виконується нерівність трикутника, бо 20 см = 1 см + 19 см.
Відповідь: може, проте не завжди.
Завдання 537
Чи існує трикутник з периметром 20 см, одна сторона якого на 2 см більша за другу і на 4 см менша від третьої?
Короткий запис
І — ?
ІІ — ?, на 2 см менша, ніж І
ІІІ — ?, на 4 см більша, ніж І
Р — 20 см
Нехай х (см) – перша сторона, тоді х – 2 (см) – друга сторона, х + 4 (см) – третя сторона. Складемо рівняння.
х + (х – 2) + (х + 4) = 20
х + х – 2 + х + 4 = 20
3х + 2 = 20
3х = 20 – 2
3х = 18
х = 18 : 3
х = 6 (см) – перша сторона.
х – 2 = 6 – 2 = 4 (см) – друга сторона.
х + 4 = 6 + 4 = 10 (см) – третя сторона.
Для найбільшої сторони не виконується нерівність трикутника, бо 10 см = 6 см + 4 см.
Відповідь: трикутник не існує.
Завдання 538
Чи існує трикутник з периметром 23 см, одна сторона якого на 6 см менша від другої і на 1 см більша за третю?
Короткий запис
І — ?
ІІ — ?, на 6 см більша, ніж І
ІІІ — ?, на 1 см менша, ніж І
Р — 23 см
Нехай х (см) – перша сторона, тоді х + 6 (см) – друга сторона, х – 1 (см) – третя сторона. Складемо рівняння.
х + (х + 6) + (х – 1) = 23
х + х + 6 + х – 1 = 23
3х + 5 = 23
3х = 23 – 5
3х = 18
х = 18 : 3
х = 6 (см) – перша сторона.
х + 6 = 6 + 6 = 12 (см) – друга сторона.
х – 1 = 6 – 5 = 1 (см) – третя сторона.
Для найбільшої сторони не виконується нерівність трикутника, бо 12 см > 6 см + 1 см.
Відповідь: трикутник не існує.
Вправи для повторення
Завдання 539
Знайдіть кути трикутника ABC, якщо кут A втричі менший від кута B і на 15° більший за кут C.
Короткий запис
∠А — ?
∠В — ?, у 3 рази більший, ніж ∠А
∠С — ?, на 15° менший, ніж ∠А
Всього — 180°
Нехай х (°) – ∠А, тоді 3х (°) – ∠В, х – 15 (°) – ∠С. Складемо рівняння.
х + 3х + (х – 15) = 180
х + 3х + х – 15 = 180
5х – 15 = 180
5х = 180 + 15
5х = 195
х = 195 : 5
х = (150 + 45) : 5
х = 39 (°) – ∠А.
3х = 39 • 3 = 117 (°) – ∠В.
х – 15 = 39 – 15 = 24 (°) – ∠С.
Відповідь: 24°, 39°, 117°.
Завдання 540 Доведіть, що два прямокутних трикутники між собою рівні, якщо висота, проведена до гіпотенузи, і катет одного трикутника дорівнюють відповідно висоті, проведеній до гіпотенузи, і катету другого трикутника.
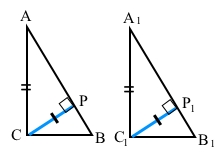
За умовою трикутники АВС і А1В1С1 – прямокутні, ∠С = ∠С1 = 90°. Катети АС = А1С1.
СР – висота до гіпотенузи, СР ﬩ АВ. С1Р1 – висота до гіпотенузи, С1Р1 ﬩ А1В1. За умовою висоти до гіпотенуз СР = С1Р1. Прямокутні трикутники ∆САР = ∆С1А1Р1 (за катетом і гіпотенузою), тому відповідні кути рівні ∠А = ∠А1. Отже, трикутники ∆АВС = ∆А1В1С1 (за катетом і прилеглим кутом), що треба було довести.
Завдання 541 Циферблат морських компасів поділено на 32 рівні частини, які називають румбами. Скільки градусів становлять 4 румби?
1) 360 : 32 = 11,25 (°) – градусна міра 1 румба.
2) 11,25 • 4 = 45 (°) – градусна міра 4 румбів.
Відповідь: 45°.
Підготуйтеся до вивчення нового матеріалу
Завдання 542 Накресліть коло із центром у точці О, радіус якого дорівнює 25 мм. Проведіть діаметр кола АВ та позначте точку M, що належить колу.
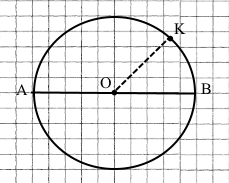
1) Виміряйте довжину діаметра AB та порівняйте її з радіусом.
ОВ = 25 мм
АВ = 5 см = 50 мм
АВ = 2ОВ
2) Виміряйте градусну міру кута AMB.
∠АMB = 47°
Поміркуй одначе
Завдання 543
1) Коник-стрибунець може переміщуватися вздовж даної прямої на 4 см або 6 см (у будь-який бік). Чи зможе він за кілька стрибків опинитися в точці, що міститься від початкової на відстані 2024 см?
Коник стрибає по прямій на 4 або 6 см, тому в результаті він перемішується на парне число сантиметрів.
2024 см – непарне число, тому коник може опинитися у цій точці.
2) Коник-стрибунець може переміщуватися вздовж даної прямої на 4 см або 6 см (у будь-який бік). Чи зможе він за кілька стрибків опинитися в точці, що міститься від початкової на відстані 2025 см?
Коник стрибає по прямій на 4 або 6 см, тому в результаті він перемішується на парне число сантиметрів.
2025 см – непарне число, тому коник не може опинитися у цій точці.