Інші завдання дивись тут...

Завдання 401 Рівняння

1) 31 • 20 = 620	42 • 200 = 8400	20 000 : 100 = 200	400 • 12 = 4800
х : 200 = 200 х = 200 • 200 х = 40000	х • 200 = 200 х = 200 : 200 х = 1	х – 200 = 200 х = 200 + 200 х = 400	200 + х = 200 х = 200 – 200 х = 0

Завдання 402

1) Для приготування вітамінного напою взяли 4 кг зелених яблук і 6 кг червоних за одна­ковою ціною. За зелені яблука заплатили 80 грн. Скільки гривень заплатили за червоні? Короткий запис 4 кг — 80 грн 6 кг — ? Розв’язання 1) 80 : 4 = 20 (грн) – ціна яблук; 2) 20 • 6 = 120 (грн) – вартість червоних яблук. Відповідь: 120 гривень.

2) Купили 6 кг червоних і 4 кг зелених яблук за однаковою ціною. За всю покупку заплатили 200 грн. Скільки коштують окремо зелені й червоні яблука? Короткий запис 4 кг — ? грн 6 кг — ? грн Разом — 200 грн Розв’язання 1) 4 + 6 = 10 (кг) – всього яблук купили; 2) 200 : 10 = 20 (грн) – ціна яблук; 3) 20 • 6 = 120 (грн) – коштують червоні яблука; 4) 20 • 4 = 80 (грн) – коштують зелені яблука. Відповідь: 120 гривень і 80 гривень.

Завдання 403

На підприємстві з виробництва екологічно чис­тої продукції за зміну виготовили 25 200 папе­рових стаканчиків. До обіду працювали 4 год, а після обіду — 3 год з такою самою продук­тивністю. Скільки стаканчиків виготовили до обіду та після обіду?

	Продуктивність праці	Час	Загальний виробіток
До обіду	?, однаково	4 год	?	25 200 ст.
Після обіду		3 год	?

Розв’язання

1–й спосіб

1) 4 + 3 = 7 (год) – весь час роботи:

2) 25200 : 7 = 3600 (ст.) – виготовили за 1 год;

3) 3600 • 4 = 14400 (ст.) – виготовили до обіду;

4) 3600 • 3 = 10800 (ст.) – виготовили після обіду.

2–й спосіб

1) 4 + 3 = 7 (год) – весь час роботи:

2) 25200 : 7 = 3600 (ст.) – виготовили за 1 год;

3) 3600 • 4 = 14400 (ст.) – виготовили до обіду;

4) 25200 – 14400 = 10800 (ст.) – виготовили після обіду.

Відповдіь: виготовили 14400 стаканчиків до обіду і 10800 стаканчиків після обіду.

Підготуйте для молодших школярів доповідь про екологічно чисту продукцію.

 

Завдання 404

На одному обладнанні виготовляють за 1 хв 80 паперових стаканчиків, а на іншому за той самий час — 120. Усього виготовили 40 200 шт. Скільки стаканчиків виготовили на обладнанні кожного виду?

	Виготовляють за 1 хв	Час	Загальний виробіток
I	80 ст.	?, однаковий	?	40 200 ст.
II	120 ст.		?

Розв’язання

1–й спосіб

1) 120 + 80 = 200 (ст) – виготовляють на двох обладнаннях за 1 хв;

2) 40200 : 200 = 402 : 2 = 201 (хв) – час виготовлення кожного стаканчика;

3) 80 • 201 = 16080 (ст.) – виготовили на першому обладнанні;

4) 120 • 201 = 24120 (ст.) – виготовили на другому обладнанні.

2–й спосіб

1) 120 + 80 = 200 (ст) – виготовляють на двох обладнаннях за 1 хв;

2) 40200 : 200 = 402 : 2 = 201 (хв) – час виготовлення кожного стаканчика;

3) 80 • 201 = 16080 (ст.) – виготовили на першому обладнанні;

4) 40200 – 16080 = 24120 (ст.) – виготовили на другому обладнанні.

Відповідь: виготовили 16080 стаканчиків на першому обладнанні і 24120 стаканчиків на другому обладнанні.

 

Завдання 405 Письмове множення

Завдання 406 Добери по 3 значення х, для яких нерівності правильні.

х • 18 > 400, якщо х = 30, 40, 50

200 – х < 175, якщо х = 30, 40, 50

x : 20 < 50, якщо х = 20, 40, 80

 

Завдання 407

Водій автомобіля помітив, що лічильник показує числовий па­ліндром (число, яке читається однаково в обох напрямках) кіло­метрів 26 962. Через 2 год на лі­чильнику було знову число–паліндром. Яка могла бути найменша постійна швидкість автомобіля?

Розв’язання

Наступний найменший паліндром після 26962, може бути 27072, тому

1) 27072 – 26962 = 110 (км) – проїхав відстань за 2 год;

2) 110 : 2 = 55 (км/год) – могла би бути найменша постійна швидкість.

Відповідь: 55 км/год.

Задача із числовими паліндромами.

1) Водій автомобіля помітив, що лічильник показує числовий па­ліндром (число, яке читається однаково в обох напрямках) кіло­метрів 15 951. Через 2 год на лі­чильнику було знову число–паліндром. Яка могла бути найменша постійна швидкість автомобіля?

Наступний найменший паліндром після 15951, може бути 16061, тому

1) 16061 – 15951 = 110 (км) – проїхав відстань за 2 год;

2) 110 : 2 = 55 (км/год) – могла би бути найменша постійна швидкість.

Відповідь: 55 км/год.

2) Андрію зараз 11 років (число є паліндромом). Скільки років його старшому братові, якщо його вік — це наступне число–паліндром? Старшому братові 22 років.

 

Завдання 408

Побудуй прямокутник довжиною 6 см і шири­ною 2 см. Проведи дві прямі так, щоб прямо­кутник поділився на 2 трикутники й 2 чотири­кутники.

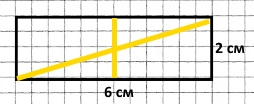
Завдання 409 

Закупили однакову кількість гофрованих кольорових стаканчиків по 4 грн і білих за ціною 2 грн. За всю покупку заплатили 60 грн. Скільки коштують окремо кольорові гофровані й білі стаканчики?

	Ціна	Кількість	Загальний вартість
Кольорові	4 грн	?, однаковий	?	60 грн
Білі	2 грн		?

Розв’язання

1–й спосіб

1) 4 + 2 = 6 (грн) – ціна стаканчиків двох видів разом;

2) 60 : 6 = 10 (ст.) – кількість кожного виду.

3) 10 • 4 = 40 (грн) – вартість кольорових стаканчиків;

4) 10 • 2 = 20 (грн) – вартість білих стаканчиків.

2–й спосіб

1) 4 + 2 = 6 (грн) – ціна стаканчиків двох видів разом;

2) 60 : 6 = 10 (ст.) – кількість кожного виду.

3) 10 • 4 = 40 (грн) – вартість кольорових стаканчиків;

4) 60 – 40 = 20 (грн) – вартість білих стаканчиків.

Відповідь: вартість 40 грн кольорових стаканчиків і 20 грн білих стаканчиків.

 

Завдання 410 Порядок дій

Завдання 411 Одиниці вимірювання

Завдання 412 Розглянь способи усного множення круглих чисел

1) 800 • 60 = 8 с. • (6 • 10) = 8 с. • 6 • 10 = 480 с. = 48 000

2) 800 • 60 = 8 • 100 • 6 • 10 = 8 • 6 • 100 • 10 = = 48 • 1000 = 48 000

 

Завдання 413

Завдання 414

Завдання 415

До мережі магазинів будматеріалів завезли 60 мішків цементу й 80 мішків сухих сумішей для штукатурки. Маса мішка цементу 50 кг, а маса мішка штукатурки — у 2 рази менша. Знайди загальну масу мішків цементу й шту­катурки.

	Маса 1 мішка	Кількість мішків	Загальна  маса
Цемент	50 кг	60	?	?
Суміші	?, у 2 рази менше	80	?

Розв’язання

1) 50 • 60 = 3000 (кг) – маса цементу;

2) 50 : 2 = 25 (кг) – маса мішка сухих сумішей;

3) 25 • 80 = 2000 (кг) – маса сухих сумішей.

4) 3000 + 2000 = 5000 (кг)

Відповідь: загальна маса мішків цементу й шту­катурки 5000 кг.

 

Завдання 416 Знаходження дробу від числа

У будівельному супермаркеті було 240 упако­вок ламінату. Першого дня продали 2/5 усіх упаковок, а другого — 2/3 кількості упаковок, проданих першого дня. На скільки більше продали упаковок ламінату першого дня, ніж другого?

Короткий запис

Усіх — 240 уп.

І — 2/5 від усіх

ІІ — 2/3 уп., проданого I

Розв’язання

1) 240 : 5 • 2 = 48 • 2 = 96 (уп.) – продали І дня;

2) 96 : 3 • 2 = 32 • 2 = 64 (уп.) – продали ІІ дня;

3) 96 – 64 = 32 (уп.) – на стільки більше упаковок продали I дня.

Відповідь: на 32 упаковки ламінату більше продали першого дня, ніж другого.

 

Завдання 417

Придбали 20 рулонів світлих шпалер та 10 рулонів темних шпалер за однаковою ціною. Яка вартість окремо кожного виду шпалер, якщо вартість покупки становила 3600 грн?

Шпалери	Ціна	Кількість рулонів	Загальна  вартість
Світлі	?, однакова	20	?	3600 грн
Темні		10	?

Розв’язання

1–й спосіб

1) 20 + 10 = 30 (р.) – всього рулонів шпалер придбали;

2) 3600 : 30 = 360 : 3 = 120 (грн) – ціна рулону шпалер;

3) 120 • 20 = 12 • 2 • 100 = 2400 (грн) – вартість світлих шпалер;

4) 120 • 10 = 1200 (грн) – вартість темних шпалер.

2–й спосіб

1) 20 + 10 = 30 (р.) – всього рулонів шпалер придбали;

2) 3600 : 30 = 360 : 3 = 120 (грн) – ціна рулону шпалер;

3) 120 • 20 = 12 • 2 • 100 = 2400 (грн) – вартість світлих шпалер;

4) 3600 – 2400 = 1200 (грн) – вартість темних шпалер.

Відповідь: вартість 2400 грн світлих шпалер  і 1200 грн темних шпалер.

 

Завдання 418 Порівняй вирази

480 • 500 = 480 • 5 • 100

270 • 4 + 270 • 10 < 270 • 40, бо 270 • 4 + 270 • 10 = 270 • (4 + 10) = 270 • 14 

720 • 16 < 720 • 10 • 6, бо 270 • 10 • 60 = 270 • 60 

310 • 12 = 310 • 10 + 310 • 2, бо 310 • 10 + 310 • 2 = 310 • (10 + 2) = 310 • 12 

 

Завдання 419

Накресли прямокутник, довжина якого 8 см, а ширина становить 1/4 довжини. Поділи його двома прямими на 2 трикутники та один п'ятикутник.

Короткий запис

Довжина — 8 см

Ширина — ?, 1/4 довжини 

8 : 4 • 1 = 2 (см) – ширина прямокутника.

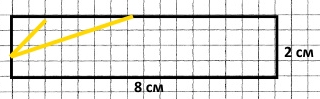
Завдання 420

Якщо додати обидва доданки й суму, то одер­жимо 400. Знайди доданки, якщо один на 20 менший від другого.

Розв’язання

1–й спосіб

1) 20 + 20 = 40 – на стільки більший перший доданок і сума разом;

2) 400 – 40 = 360 – сума трьох однакових доданків;

3) 360 : 3 = 90 – перший доданок;

4) 90 + 20 = 110 – другий доданок.

2–й спосіб

Нехай перший доданок дорівнює х, тоді другий доданок — (х – 20), а їхня сума — (х + х – 20). Складаємо рівняння:

х + (х – 20) + х + (х – 20) = 400

х + х – 20 + х + х – 20 = 400

4 • х – 40 = 400

4 • х = 400 + 40

4 • х = 440

х = 440 : 4

х = 110 – перший доданок;

110 – 20 = 90 – другий доданок.

3–й спосіб

Нехай другий доданок дорівнює х, тоді перший доданок — (х + 20), а їхня сума — (х + х + 20). Складаємо рівняння:

х + (х + 20) + х + (х + 20) = 400

х + х + 20 + х + х + 20 = 400

4 • х + 40 = 400

4 • х = 400 – 40

4 • х = 360

х = 360 : 4

х = 90 – другий доданок;

90 + 20 = 110 – перший доданок.

Відповідь: перший доданок дорівнює 110, другий — 90.

 

Завдання 421

Два автомобілі разом привозили на будів­ництво за один рейс по 20 т бетону. За однакову кількість рейсів перший доставив 72 т бетону, а другий — 48 т. Яка вантажність кожного автомобіля?

Автомобілі	Вантажність 1 автомобіля		Кількість рейсів	Всього перевезли
I	?	20 т	?, однакова	72 т
II	?			48 т

Розв’язання

1–й спосіб

1) 72 + 48 = 120 (т) – всього бетону перевезли;

2) 120 : 20 = 6 (р.) – робив кожен автомобіль;

3) 72 : 6 = (60 + 12) : 6 = 10 + 2 = 12 (т) – вантажність I автомобіля;

4) 48 : 6 = 8 (т) – вантажність II автомобіля.

2–й спосіб

1) 72 + 48 = 120 (т) – всього бетону перевезли;

2) 120 : 20 = 6 (р.) – робив кожен автомобіль;

3) 72 : 6 = (60 + 12) : 6 = 10 + 2 = 12 (т) – вантажність I автомобіля;

4) 20 – 12 = 8 (т) – вантажність II автомобіля.

Відповідь: вантажність 12 т першого автомобіля і 8 т другого автомобіля.

 

Завдання 422

Інші завдання дивись тут...