Завдання 290 Порядок дій
780 – 180 : 2 • 6 = 780 – 90 • 6 = 780 – 540 = 240
(800 : 8 – 20) : 4 = (100 – 20) : 4 = 80 : 4 = 20
(780 – 180) : 2 • 6 = 600 : 2 • 6 = 300 • 6 = 1800
800 : 8 – 20 : 4 = 100 – 5 = 95
Завдання 291 Дроби
Довжина 3/5 відрізка AB дорівнює 6 см. Яка довжина всього відрізка AB?
Розв'язання
1) Скільки сантиметрів в 1/5 — відрізка AB? 6 : 3 = 2 (см)
2) Яка довжина відрізка AB? 2 • 5 = 10 (см)
Відповідь: довжина відрізка AB дорівнює 10 см.
Завдання 292
Туристи пройшли 8 км, що становить 1/3 маршруту. Яка довжина всього маршруту?
Розв'язання
8 • 3 = 24 (км) – довжина всього маршруту.
� Зміни запитання, щоб у розв'язанні добавилося 2 дії:
а) віднімання і віднімання;
На скільки більше кілометрів залишилося пройти туристам, ніж вони вже встигли пройшли?
Розв'язання
1) 8 • 3 = 24 (км) – довжина всього маршруту
2) 24 - 8 = 16 (км) – залишилося пройти
3) 16 - 8 = 8 (км) – на стільки більше залишилося пройти, ніж вони вже встигли пройти.
Відповідь: туристам залишилося пройти на 8 кілометрів більше, ніж вони вже встигли пройти.
б) віднімання і ділення.
У скільки разів більше кілометрів залишилося пройти туристам, ніж вони вже встигли пройшли?
Розв'язання
1) 8 • 3 = 24 (км) – довжина всього маршруту
2) 24 - 8 = 16 (км) – залишилося пройти
3) 16 : 8 = 2 (рази) – у стільки більше залишилося пройти, ніж вони вже встигли пройти.
Відповідь: туристам залишилося пройти у 2 рази більше кілометрів, ніж вони вже встигли пройти.
Завдання 293
Автотуристи проїхали по ґрунтовій дорозі 240 км, що становило 2/3 відстані по асфальтовій дорозі. Скільки часу вони були в дорозі, якщо по асфальтовій дорозі за 1 год проїжджали 90 км, а по ґрунтовій — 60 км?
Розв'язання
1) 240 : 2 • 3 = 360 (км) – відстань асфальтової дороги
2) 240 : 60 = 4 (год) – час на ґрунтовій дорозі
3) 360 : 90 = 4 (год) – час на асфальтовій дорозі
4) 4 + 4 = 8 год
Відповідь: автотуристи були в дорозі 8 годин.
Завдання 294
1) 1 л соку налили у склянки місткістю 1/5 л кожна. Скільки таких склянок використали?
Розв'язання
5 склянок. (5/5 = 1)
2) 4 л молока налили в півлітрові банки. Скільки банок використали?
Розв'язання
Півлітрова банка 1/2 л, тому щоб розлити 1 літру молока, треба 2 банки.
4 • 2 = 8 (банок) – використали банок для 4 л молока.
Завдання 295
Якщо а = 120, тоді (а • 4 – а : 24) • 2 = (120 • 4 – 120 : 24) • 2 = (480 – 5) • 2 =
= 475 • 2 = 950
Завдання 296 Знайди периметр прямокутної ділянки, ширина якої 24 м, що становить 3/8 довжини.
24 : 3 • 8 = 64 (м) – довжина прямокутної ділянки.
Р = (24 + 64) • 2 = 88 • 2 = (80 + 8) • 2 = 160 + 16 = 176 (м) – периметр прямокутної ділянки.
Завдання 297 Ділене зменшили у 2 рази, а дільник зменшили на 6, але частка не змінилася. Знайди дільник.
Розв'язання
Якщо ділене зменшити у 2 рази, тоді частка зменшиться у 2 рази. Але частка також зменшиться у 2 рази, якщо дільник збільшити у 2 рази.
Нехай х – ділене, складемо рівняння змін з діленим:
2 • (х – 6) = х
2 • х – 12 = х
2 • х – х = 12
х • (2 – 1) = 12
х = 12
Відповідь: ділене дорівнює 12.
Завдання 298
2/5 від 1 кг = 1 кг : 5 • 1 = 1000 г : 5 = 200 г
3/4 від 1 год = 2 хв : 3 • 1 = 2 • 60 с : 3 = 120 с : 3 = 40 с
4/5 від 1 м = 1 год : 4 • 1 = 60 хв : 4 = 15 хв
Завдання 299 Автобус на 100 км витрачає 14 л пального. Скільки потрібно пального легковому автомобілю на 400 км, якщо на 100 км він витрачає 4/7 від кількості пального, яке витрачає автобус?
Розв'язання
1) 14 : 7 • 4 = 2 • 4 = 8 (л) – витрачає автомобіль на 100 км
2) 400 : 100 = 4 (рази) – стільки разів по 100 км міститься в 400 км
3) 4 • 8 = 32 (л)
Відповідь: легковому автомобілю потрібно 32 л на 400 км.
Завдання 300
|
765 : 3 + 812 : 4 = 458
|
_765 | 3 6 255 _16 15 _15 15 0 |
_812 | 4 8 203 _12 12 0 |
+255 203 458 |
|
476 : 28 • 36 – 18 • 32 = 612 – 576 = 36 |
_476 | 28 28 17 _196 196 0 |
х 17 36 102 51 612 |
х 18 32 36 54 576 |
Завдання 301
1) Знайди:
3/4 від 1 год = 1 год : 4 • 3 = 60 хв : 4 • 3 = 45 хв
3/5 від 1 год = 1 год : 5 • 3 = 60 хв : 5 • 3 = 36 хв
1/6 від 1 год = 1 год : 6 • 1 = 60 хв : 6 • 1 = 10 хв
5/6 від 1 год = 1 год : 6 • 5 = 60 хв : 6 • 5 = 50 хв
5/12 від 1 год = 1 год : 12 • 5 = 60 хв : 12 • 5 = 25 хв
1/20 від 1 год = 1 год : 20 • 1 = 60 хв : 20 • 1 = 3 хв
2) Число, 3/5 якого дорівнює 60.
60 : 3 • 5 = 100
Завдання 302 Хлопчик на 5/6 усіх своїх грошей купив 2 книжки, за ціною 30 грн кожна. Скільки грошей було в хлопчика спочатку?
Розв'язання
1) 30 • 2 = 60 (грн) – заплатив за книжки
2) 60 : 5 • 6 = 12 • 6 = 72 (грн)
Відповідь: у хлопчика було спочатку 72 грн.
Завдання 303 4 хлопчики зібрали в лісі 3 кг ожини та поділили її порівну. Скільки ожини одержав кожний хлопчик?
Розв'язання
1 спосіб
3 : 4 = 3/4 (кг) = 750 (г)
2 спосіб
1 кг = 1000 г, 1000 : 4 • 3 = 750 (г)
Завдання 304 За 4 дні дівчинка прочитала 64 сторінки книжки, а залишилося читати 2/3 кількості сторінок. За скільки днів вона закінчить читати всю книжку, якщо за день читатиме по стільки само сторінок?
Розв'язання
1-й спосіб
1) 64 • 3 = 192 (стор.) – всього сторінок
2) 192 - 64 = 128 (стор.) – залишилося прочитати
3) 64 : 4 = 16 (стор.) – читає за один день
4) 128 : 16 = 8 (днів)
2-й спосіб
Якщо залишилося читати 2/3 кількості сторінок, то прочитаних 1/3 кількості сторінок становить 64 сторінки, тоді на решту сторінок витратить удвічі більше часу:
4 • 2 = 8 (днів)
Відповідь: дівчинка закінчить читати всю книжку за 8 днів.
Завдання 305 Довжина садиби 100 м, а ширина — на 60 м менша. 3/8 площі садиби займають будівлі, двір і сад, а решту — город. Яку площу займає город?
Розв'язання
1) 100 – 60 = 40 (м) – ширина садиби
2) 100 • 40 = 4000 (м2) – площа садиби
3) 4000 : 8 • 3 = 1500 (м2) – площу займають будівлі, двір, сад
4) 4000 – 1500 = 2500 (м2)
Відповідь: город займає 2500 м2.
Завдання 306
1/3 доби < 6 год (1/3 від доби = 12 год : 3 • 1 = 4 год, а 4 год < 6 год)
Порівняй 1/5 т = 2 ц (1/5 т = 10 ц : 5 • 1 = 2 ц, а 2 ц = 2 ц)
Порівняй 1/4 км > 300 м (1/4 км = 1000 м : 4 • 1 = 250 м, а 250 м > 300 м)
Порівняй 1/20 м > 1 см (1/20 м = 100 м : 20 • 1 = 5 м, а 5 м > 1 см)
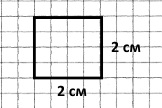
Завдання 307 Побудуй квадрат, периметр якого дорівнює 2/5 периметра трикутника зі сторонами 6 см, 8 см, 6 см.
1) 6 + 8 + 6 = 20 (см) – периметр трикутника
2) 20 : 5 • 2 = 8 (см) – периметр квадрата
3) 8 : 4 = 2 (см) – сторона квадрата
Завдання 308
|
Нерівність |
х менше рівне 402 |
х більше рівне 325 |
х менше рівне 73 |
|
Найменше значення |
0 |
325 |
0 |
|
Найбільше значення |
402 |
натуральний ряд нескінчений |
73 |
Завдання 309 У чотирьох класах 126 учнів. В одному класі на 10 учнів більше, ніж у кожному з інших трьох. Скільки учнів у кожному із цих класів?
Розв'язання
1) 126 – 10 = 116 (уч.) – у чотирьох класах порівно.
2) 116 : 4 = (80 + 36) : 4 = 29 (уч.) – у кожному з трьох інших класів.
3) 29 + 10 = 39 (уч.) – в одному з класів.
Відповідь: у трьох класах по 29 учнів, а в одному з класів 39 учнів.
Завдання 310
|
1) (825 : 3 + 850 : 5) : 5 = =(400 + 45) : 5 = 80 + 9 = = 89 |
_825 | 3 6 275 _22 21 15 15 0 |
_850 | 5 5 170 _35 35 0 |
+275 170 445
|
|
825 : 3 + 850 : 5 : 5 = = 275 + 34 = 309 |
_825 | 3 6 275 _22 21 15 15
0 |
_850 | 5 5 170 _35 35
0 |
_170 | 5 15 34 _20 20 0 |
|
2) х – 470 = 660 : 3 х – 470 = 220 х = 220 + 470 х = 690 |
600 – 2 • х = 460 2 • х = 600 – 460 2 • х = 140 х = 140 : 2 х = 70 |
|
|
Завдання 311
1) 2/3 від 69 = 69 : 3 • 2 = 23 • 2 = 46
3/4 від 72 = 72 : 4 • 3 = 18 • 2 = 36
4/5 від 65 = 65 : 5 • 4 = 13 • 4 = 52
6/7 від 63 = 63 : 7 • 6 = 9 • 2 = 18
2) якщо 2/5 а = 10, тоді а = 10 : 2 • 5 = 25
Якщо 3/4 а = 12, тоді а = 12 : 3 • 4 = 16
Якщо 2/3 а = 18, тоді а = 18 : 2 • 3 = 27
Завдання 312
9/9 = 1 7/7 = 1 4/4 = 1 6/6 = 1 10/10 = 1
Завдання 313
Для виготовлення хліба на опарі борошна беруть а кг, води – 7/10 маси борошна, солі 1/40 маси борошна. Знайди масу тіста.
Вираз: а + а : 10 • 7 + а : 40 • 1
Якщо а = 40 кг, тоді
40 + 40 : 10 • 7 + 40 : 40 • 1 = 40 + 28 + 1 = 69 (кг)
Якщо а = 2 кг = 200 г, тоді
2000 + 2000 : 10 • 7 + 2000 : 40 • 1 = 2000 + 1400 + 50 = 3450 (г) = 3 кг 450 г
Завдання 314
На хлібокомбінат привезли 6 ц житнього борошна, що становить 3/8 маси всього привезеного борошна. На скільки центнерів більше привезли пшеничного борошна, ніж житнього?
Розв'язання
Завдання 315
З а кг вершків одержують b кг масла. Скільки кілограмів масла одержать із с кг вершків? Склади вираз та обчисли, якщо а = 18; с = 360; b = 4.
Короткий запис
а кг — b кг
с кг — ?
Розв'язання
Вираз: с : a • b
360 : 18 • 4 = 20 • 4 = 80 (кг)
Відповідь: одержать 80 кілограмів масла із 360 кг вершків.
Завдання 316 Рівняння
|
а • 7 – 423 = 354 а • 7 = 354 + 423 а • 7 = 777 a = 777 : 7 a = 111 |
b : 23 + 278 = 314 b : 23 = 314 - 278 b : 23 = 36 b = 36 • 23 b = 828 |
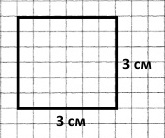
Завдання 317 Побудуй квадрат, периметр якого дорівнює периметру прямокутника із шириною 2 см, що у 2 рази менше довжини.
Короткий запис
Ширина — 2 см
Довжина — ?, у 2 рази більша за ширину
Р прямокутника — ?
Рпрямокутника = Рквадрата
Сторона — ?
Розв'язання
1) 2 • 2 = 4 (cм) – довжина прямокутника
2) (2 + 4) • 2 = 6 • 2 = 12 (см) – периметр прямокутника
3) 12 : 4 = 3 (см) – сторона квадрата.
Завдання 318
|
813 : 3 + 966 : 21 = 317 |
_813 | 3 6 271 _21 21 3 3
0 |
_966 | 21 84 46 _126 126 0 |
+271 46 317 |
|
615 : 3 – 428 : 4 = 98 |
_615 | 3 6 205 _15 15 0 |
_428 | 4 4 107 _28 28 0 |
_205 107 98 |
Завдання 319
У класі 6 дітей їдять морозиво щодня. 18 дітей їдять морозиво через день. Інші учні не їдять морозива. Учора 10 дітей їли морозиво. Скільки дітей буде їсти морозиво сьогодні?
Завдання 320
З 5 кг макулатури можна виготовити 125 шкільних зошитів. Скільки кілограмів макулатури потрібно зібрати, щоб виготовити 25 таких зошитів?
Короткий запис
Відповідь: потрібно зібрати 1 кг макулатури, щоб виготовити 25 таких зошитів.
Завдання 321 Порівняння чисел
|
27 • 13 > 43 • 6 480 : 40 > 560 : 14 |
380 : 20 < 900 : 5 36 • 24 > 25 • 26 |