Інші завдання дивись тут... 

Завдання 289 Множення

5 • 11 • 100 = 5 • (10 + 1) • 100 = (50 + 5) • 100 = 55 • 100 = 5500

45 • 2 • 50 = 2 • 50 • 45 = 100 • 45 = 4500

81 • 5 • 10 = (80 + 1) • 5 • 10 = (400 + 5) • 10 = 4000 + 50 = 4050

 

Завдання 290 Письмове множення

800 • 40 = 8 • 100 • 4 • 10 = 8 • 4 • 100 • 10 = 32 000

1400 • 500 = 14 • 100 • 5 • 100 = 14 • 5 • 100 • 100 = 700000

 

Завдання 292

Добутки обчислені правильно.

 

Завдання 293

360 • 50 = 360 • 5 • 10 270 • 40 < 270 • 4 • 100 320 • 60 > 320 • 6 + 320 • 10 310 • 50 > 310 • 5 + 310 • 10

360 • 50 = 360 • 50 270 • 40 < 270 • 400 320 • 60 > 320 • (6 + 10) 310 • 50 > 310 • (5 + 10)

Завдання 295

Найменша пташка у світі — колібрі — за секунду робить до 80 помахів крилами. Скільки помахів крилами може зробити ця пташка за годину?

Короткий запис

1 с — 80 помахів

1 год (3600 с) — ? помахів

Розв'язання

1 год = 60 хв = 60 • 1 хв = 60 • 60 с = 3600 с

1) 80 • 3600 = 8 • 36 • 10 • 100 = 288 • 10 • 100 = 288000 (п.)

Відповідь: колібрі може зробити 288000 помахів за годину.

 

Завдання 296

У скільки разів площа прямокутника ABCD біль­ша, ніж площа прямокутника KLMP? Знайди площу зафарбованої частини прямокутника ABCD.

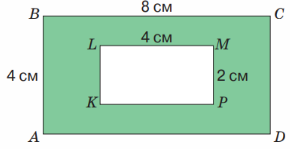
Розв'язання

1) 8 • 4 = 32 (см²) – площа прямокутника ABCD;

2) 4 • 2 = 8 (см²) – площа прямокутника KLMP;

3) 32 : 8 = 4 (р.) – у стільки разів площа прямокутника ABCD більша;

4) 32 – 8 = 24 (см²) 

Відповідь: у 4 рази площа прямокутника ABCD біль­ша, ніж площа прямокутника KLMP, площа зафарбованої частини прямокутника ABCD 24 см².

 

Завдання 297

Пішохід ішов 120 хв зі швидкістю 50 м/хв. Скільки кілометрів пройшов пішохід?

Завдання 298 Порядок дій

х 1500     300    450000

х 840     200   168000

5600 • 40 – 7310 • 30 = 4700 

х 5600     40     224000

х 7310      30    219300

_ 224000    219300       4700

(2241 : 9) • 400 = 99600

Завдання 300 Ділення

1) Спосіб зведення до розрядних одиниць.

27000 : 3000 = 27 тис. : 3 тис. = 9

2) Спосіб послідовного ділення. 

32000 : 8000 = 32000 : (8 • 1000) = 32 000 : 1000 : 8 = 32 : 8 = 4

3) Спосіб послідовного ділення. 

8400 : 70 = 8400 : (7 • 10) = 8400 : 10 : 7 = 120

 

Завдання 301

Спосіб послідовного ділення.

68000 : 400 = 68000 : (4 • 100) = 68000 : 100 : 4 = 680 : 4 = 170

4200 : 30 = 4200 : (3 • 10) = 4200 : 10 : 3 = 420 : 3 = 140

5700 : 300 = 57 сот. : 3 сот. = 19

7800 : 60 = 7800 : (6 • 10) = 7800 : 10 : 6 = 780 : 6 = 130

2 спосіб 

Спосіб зведення до розрядних одиниць. 

68 000 : 400 4200 : 30 5700 : 300 7800 : 60

68000 : 400 = 680 сот. : 4 сот. = 680 : 4 = 170

4200 : 30 = 420 дес. : 3 дес. = 420 : 3 = 140

5700 : 300 = 57 сот. : 3 сот. = 57 : 3 = 19

7800 : 60 = 780 дес. : 6 дес. = 780 : 6 = 130

 

Завдання 302 

Ділення:  24780 : 30 = 24780 : (3 • 10) = 24790 : 10 : 3 = 2479 : 3 = 826

Письмове ділення: 

Завдання 303 Письмове ділення

Назви формулу, за якою знаходять відстань, якщо відомо час і швидкість.

S = v • t

Склади й розв'яжи задачі за даними таблиці.

Тварина	Швидкість	Час	Відстань
Олень	10 км/год	3 год	? км
Акула	30 км/год	3 год	? км
Ластівка	60 км/год	3 год	? км

1) Олень пересувається зі швидкістю 10 км/год. Яку відстань він подолає за 3 год?

Короткий запис

Швидкість — 10 км/год

Час — 3 год

Відстань — ? км

Розв'язання

10 • 3 = 30 (км)

Відповідь: олень подолає 30 кілометрів.

 

2) Акула пливе зі швидкістю 30 км/год. Яку відстань вона подолає за 3 год?

Короткий запис

Швидкість — 30 км/год

Час — 3 год

Відстань — ? км

Розв'язання

30 • 3 = 90 (км)

Відповідь: акула подолає 90 кілометрів.

 

3) Ластівка летить зі швидкістю 60 км/год. Яку відстань вона подолає за 3 год? 

Короткий запис

Швидкість — 60 км/год

Час — 3 год

Відстань — ? км

Розв'язання

60 • 3 = 180 (км)

Відповідь: ластівка подолає 180 кілометрів.

Хто подолає більшу відстань за три години? Ластівка.

Чому? Має найбільшу швидкість руху.

 

Завдання 306

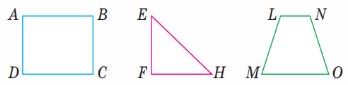
Розглянь на малюнку геометричні фігури. Зна­йди в них указані елементи:

а) гострі кути; FEH, EHF, LMО, MON;

б) прямі кути; ABC, BCD, CDA, DAB, ЕFН;

в) тупі кути (запиши їхні назви в третьому рядку): MLN, LNO.

 

Завдання 307

Потяг рухався зі швидкістю 65 км/год. До зу­пинки він був у дорозі 4 год. Решту шляху піс­ля зупинки він подолав з тією самою швидкістю за 2 год. Яку відстань подолав потяг?

	Швидкість	Час	Відстань
До зупинки	65 км/год	4 год
Після зупинки	однакова	2 год
Всього	65 км/год	? год	? км

Короткий запис

До зупинки — 4 год по 65 км/год

Після зупинки — 2 год по 65 км/год

Всього — ? км, ? год по 65 км/год 

Розв'язання

Оскільки потяг рухався з однаковою швидкістю, відстань можна знайти за загальним часом. 

1) 4 + 2 = 6 (год) – весь час;

2) 6 • 65 = 390 (км) – відстань подолав потяг. 

2 спосіб

	Швидкість	Час	Відстань
До зупинки	65 км/год	4 год	? км
Після зупинки	однакова	2 год	? км
Всього			? км

Короткий запис

До зупинки — ? км, 4 год по 65 км/год

Після зупинки — ? км, 2 год по 65 км/год

Всього — ? км

Розв’язання   

1) 65 • 4 = (60 + 5) • 4 = 260 (км) – відстань до зупинки;

2) 65 • 2 = 65 + 65 = 130 (км) – відстань після зупинки;

3) 260 + 130 = 390 (км) – відстань подолав потяг. 

Відповідь: потяг подолав 390 кілометри.

 

Завдання 308

Якщо а = 20, то 8880 : а + 1234 = 8880 : 20 + 1234 = 1678

Якщо а = 30, то 8880 : а + 1234 = 8880 : 30 + 1234 = 1530

Якщо а = 60, то 8880 : а + 1234 = 8880 : 60 + 1234 = 1382

Інші завдання дивись тут...