§ 69 Завдання 676

200 000 + 100 000 + 300 000 + 200 000 + 200 000 = 1 000 000 (євро) – премію отримала Грета Тунберг за боротьбу зі зміною клімату.

 

Завдання 677 Усього одиниць, десятків, сотень, тисяч

20 600 – 2060 дес. 329 708 – 329 708 од.

3800 – 38 сот. 430 100 – 4 сот. тис.

105 300 – 10 дес. тис. 843 000 – 843 од. тис.

Завдання 678 Віднімання чисел

56 000 – 23 000 = 56 тис. – 23 тис. = 33 тис. = 33 000

80 000 – 64 000 = 80 тис. – 64 тис. = 16 тис. = 16 000

875 000 – 340 000 = 875 тис. – 340 тис. = 535 тис. = 535 000

 

Завдання 679

2800 – 1600 = 28 сот. – 16 сот. = 12 сот. = 12 000

477 000 – 12 000 = 477 тис. – 12 тис. = 465 тис. = 465 000

98 000 – 57 000 = 98 тис. – 57 тис. = 41 тис. = 41 000

657 000 – 346 000 = 657 тис. – 346 тис. = 311 тис. = 311 000

 

Завдання 680 Рівняння

400 + х = 1500 + 2000 400 + х = 3500 х = 3500 – 400 х = 3100

78 130 + у = 88 100 + 30 78 130 + у = 88 130 у = 88 130 – 78 130 у = 10 000

Завдання 681

Два зайці бігли назустріч один одному. Швидкість руху першого зайця становила 12 м/с, а другого — 10 м/с. На скільки метрів зайці наблизились один до одного через 6 с?

Розв'язання

1–ий спосіб

1) 12 • 6 = 72 (м) – відстань подолав перший заєць через 6 с;

2) 10 • 6 = 60 (м) – відстань подолав другий заєць через 6 с;

3) 72 + 60 = 132 (м) – на таку відстань наблизились один до одного через 6 с.

2–ий спосіб

1) 12 + 10 = 22 (м) – на таку відстань наблизилися через 1 с (швидкість зближення);

2) 22 • 6 = 132 (м) – на таку відстань наблизились через 6 с.

Відповідь: на 132 м.

 

Завдання 682 Периметр прямокутника

Спортивний майданчик має форму прямокутника. Довжина майданчика дорівнює 18 м, а ширина вдвічі менша. Обчисли довжину огорожі навколо спортивного майданчика.

Короткий запис

Довжина – 18 м

Ширина – ?,  2 р. менша, ніж довжина

Р – ?

Розв'язання

1) 18 : 2 = 9 (м) – ширина прямокутника;

2) (18 + 9) • 2 = 27 • 2 = 54 (м) – периметр прямокутника.

Відповідь: довжина огорожі 15 м.

 

Завдання 683

84 000 – 27 000 = 84 дес. – 27 дес. = 57 дес. = 57 000

870 000 – 36 000 = 870 тис. – 36 тис. = 834 тис. = 834 000

8400 – 3300 = 84 сот – 33 сот. = 51 сот. =  5100

508 000 – 407 000 = 508 тис. – 407 тис. = 101 тис. = 101 000

 

Завдання 684

З міста одночасно в протилежних напрямках виїхали два автомобілі. Через 4 год відстань між ними становила 480 км. Яка швидкість першого автомобіля, якщо швидкість другого — 70 км/год?

Схематичний рисунок.

t = 4 год                  <— ? км/год             70 км/год —>           |———————————∆———————————————| 1—ий автомобіль       S = 480 км                   2—ий автомобіль

Розв'язання

1–й спосіб

1) 480 : 4 = 120 (км) – на таку відстань віддаляться автомобілі за 1 год;

2) 120 – 70 = 50 (км) – відстань проїхав I автомобіль за 1 год.

2–й спосіб

1) 70 • 4 = 280 (км) – відстань проїхав II автомобіль за 4 год;

2) 480 – 280 = 200 (км) – відстань проїхав I автомобіль за 4 год;

3) 200 : 4 = 50 (км) – відстань проїхав I автомобіль за 1 год.

Відповідь: швидкість першого автомобіля 50 км/год.

 

§ 70 Завдання 685, 686

Фігури на площині	Об'ємні фігури
квадрат (зелена фігура) круг (блакитна фігура) п'ятикутник (червона фігура) трикутник (рожева фігура) шестикутник (жовта фігура)	циліндр (жовта фіруга) куля (червона фігура) піраміда (зелена фігура) куб (синя фігура) конус (блакитна фігура)

Завдання 687

25 000 + 45 000 = 25 тис. + 45 тис. = 70 тис. = 70 000

678 000 – 237 000 = 678 тис. – 237 тис. = 441 тис. = 441 000

874 000 – 70 000 = 874 тис. – 70 тис. = 804 тис. = 804 000

67 200 + 30 400 = 672 сот. + 304 сот. = 976 сот. = 97 600

 

Завдання 688

х – 16 500 = 5300 х = 5300 + 16 500 х = 21 800

х + 4200 = 1400 + 5200 х + 4200 = 6600 х = 6600 – 4200 х = 2400

Завдання 689

Ворона пролетіла 100 км зі швидкістю 50 км/год. Скільки годин летіла ворона?

Короткий запис

Відстань – 100 км

Швидкість – 50 км/год

Час – ?

Розв'язання

100 : 50 = 2 (год)

Відповідь: ворона летіла 2 години.

 

Завдання 690

З пункту А одночасно в протилежних напрямках виїхали колісний та гусеничний трактори. Швидкість колісного трактора становить 30 км/год, а гусеничного — 10 км/год. На скільки кілометрів віддаляться один від одного трактори за 1 год? Через скільки годин відстань між ними становитиме 160 км?

Схематичний рисунок.

t = ? год                              <— 30 км/год        10 км/год —>           |———————————————∆————————————| триколісний                          S = 160 км               гусеничний

Розв'язання

1) 30 + 10 = 40 (км) – на стільки віддаляться один від одного через 1 год.

2) 160 : 40 = 4 (год) – за стільки часу віддаляться один від одного на 160 км.

Відповідь: на 40 км віддаляться один від одного трактори за 1 год, через 4 год відстань між ними становитиме 160 км.

 

Завдання 691

Порівняння виразів	Дії з іменованими величинами
520 мм > 50 см + 2 мм 14 см < 10 дм + 8 см 100 мм + 900 мм = 1 м 100 дм > 1 м – 10 см 16 ц – 70 кг > 80 кг 200 г + 100 г < 3 кг	50 см + 2 мм = 500 мм + 2 мм = 502 мм 10 дм + 8 см = 100 см + 8 см = 108 см 100 мм + 900 мм = 1000 мм = 1 м 1 м – 10 см = 10 дм – 1 дм = 9 дм 16 ц – 70 кг = 1600 кг – 70 кг = 1530 кг 200 г + 100 г = 300 г

Завдання 692

49 000 – 27 000 = 49 тис. – 27 тис. = 22 тис. = 22 000

385 000 – 23 000 = 385 тис. – 23 тис. = 362 тис. = 362 000

7400 + 11 500 = 74 сот. + 115 сот. = 189 сот. = 18 900

18 900 + 1100 = 189 сот + 11 сот = 200 сот. = 20 000

 

Завдання 693

Два велосипедисти рухалися назустріч один одному. Швидкість першого велосипедиста дорівнює 15 км/год, а швидкість другого — 14 км/год. На скільки кілометрів велосипедисти наблизяться один до одного через 2 год?

Схематичний рисунок.

15 км/год —>                         t = 2 год               <— 14 км/год        |——————————————∆———————————|  I велосипедист                      S = ? км                II велосипедист

Розв'язання

1–ий спосіб

1) 15 • 2  = 30 (км) – відстань подолав перший велосипедист за 2 год;

2) 14 • 2  = 28 (км) – відстань подолав другий велосипедист за 2 год.

3) 30 + 28 = 58 (км) 

2–ий спосіб

1) 15 + 14 = 29 (км) – на таку відстань наблизяться через 1 год;

2) 29 • 2 = 58 (км) – на таку відстань наблизяться через 2 год.

Відповідь: на 58 км велосипедисти наблизяться один до одного через 2 год.

 

§ 71 Завдання 694

500 + 300 + 200 + 60 + 1000 + 1 = 2061 (м) – висота Говерли — найвищої вершини Українських Карпат.

 

Завдання 695 Порівняння

У порядку зростання: 2228 м, 4810 м, 4892 м, 5895 м, 6961 м, 8848 м

 

Завдання 696

896 000 – 90 000 = 896 тис. – 90 тис. = 806 тис. = 806 000

489 000 – 267 000 = 489 тис. – 267 тис. = 222 тис. = 222 000

47 000 + 2400 = 470 сот. + 24 сот. = 494 сот. = 49 400

36 100 + 23 400 = 361 сот. + 234 сот. = 595 сот. = 59 500

 

Завдання 697 Рівняння

34 000 – х = 2400 + 1600 34 000 – х = 4000 х = 34 000 – 4000 х = 30 000

у + (27 200 + 2100) = 39 300 у + 29 300 = 39 300 у = 39 300 – 29 300 у = 10 000

Завдання 698 

До місця призначення автомобіль їхав 3 год зі швидкістю 72 км/год. Зворотний шлях він подолав за 4 год. З якою швидкістю рухався автомобіль у зворотному напрямку?

	Швидкість	Час	Відстань
Прямий шлях	72 км/год	3 год	?
Зворотний шлях	? км/год	4 год

Розв'язання

1) 72 • 3 = 216 (км) – відстань;

2) 216 : 4 = 54 (км/год)

Відповідь: швидкість автомобіля у зворотному напрямку 54 км/год.

 

Завдання 699

Велосипедист був у дорозі 4 год, а мотоцикліст — 3 год. На скільки кілометрів більше проїхав мотоцикліст, якщо велосипедист рухався зі швидкістю 14 км/год, а мотоцикліст — 50 км/год?

1) Яку відстань проїхав велосипедист за 4 год?

2) Яку відстань проїхав мотоцикліст за 3 год?

3) На скільки кілометрів більше проїхав мотоцикліст, ніж велосипедист?

Розв'язання

1) 14 • 4 = 56 (км) – відстань проїхав велосипедист за 4 год;

2) 50 • 3 = 150 (км) – відстань проїхав мотоцикліст за 3 год.

3) 150 – 56 = 94 (км)

Відповідь: на 94 км більше проїхав мотоцикліст, ніж велосипедист.

 

Завдання 700

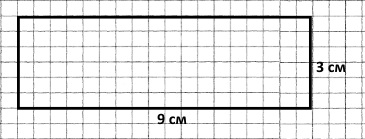
Знайди периметр прямокутника зі сторонами 9 см і 3 см. Побудуй цей прямокутник.

(9 + 3) • 2 = 12 • 2 = 24 (см) – периметр прямокутника.

Завдання 701 Рівняння

х – 1800 = 20 100 х = 20 100 + 1800 х = 21 900

42 000 + х = 256 000 х = 256 000 – 42 000 х = 214 000

Завдання 702

Якщо рухатися по Дніпру, то відстань між Києвом і Каневом становить 120 км. Тривалість подорожі на «ракеті» від Києва до Канева й назад — 4 год. З якою швидкістю рухається «ракета»?

	Швидкість	Час	Загальна відстань
Від Києва до Канева	?	4 год	120 км	?
Від Канева до Києва			?, однакова

Розв'язання

1) 120 + 120 = 240 (км) – відстань вперед і назад.

2) 240 : 4 = 60 (км/год)

Відповідь: «ракета» рухається зі швидкістю 60 км/год.

 

ПЕРЕВІРЯЄМО СВОЇ ДОСЯГНЕННЯ
Завдання 703

Число 31 700 має п'ять цифр, отже, є пятицифрове, тому Б п’ятицифрове

 

Завдання 704

У класі одиниць лічать одиницями, тому А одиницями

 

Завдання 705 Принцип групування розрядів у класи

У числі 729 002 є клас одиниць і клас тисяч, тому В першого та другого класів

 

Завдання 706 Усього десятків тисяч у числі

Загальна кількість десятків тисяч у числі 273 440 є 27, тому Б 27

 

Завдання 707

У розряді сотень тисяч числа 541 931 стоїть цифра 5, тому Б 5

 

Завдання 708

40 700 – 4070 дес. 911 008 – 911 008 од. 32 400 – 324 сот.

640 300 – 64 сот. тис. 109 800 – 10 дес. тис. 542 000 – 542 од. тис.

Завдання 709

5000 + 2000 + 300 = 50 сот. + 20 сот. + 3 сот. = 73 сот. = 7300

6000 + 1000 + 7 = 6 тис. + 1 тис. + 7 од. = 7 тис. + 7 од. = 7000 + 7 = 7007

90 000 – 50 000 + 2000 = 90 тис. – 50 тис. + 2 тис. = 42 тис. = 42 000

1000 – 100 – 1 = 10 сот. – 1 сот. – 1 од. = 9 сот. – 1 од. = 900 – 1 = 899

 

Завдання 710  Рівняння

45 000 – х = 3400 + 1600 45 000 – х = 5000 х = 45 000 – 5000 х = 40 000

у + (36 200 + 3200) = 49 400 у + 39400 = 49 400 у = 49 400 – 39 400 х = 10 000

Завдання 711

Порівняння виразів	Дії з іменованими величинами
740 мм 7 > 0 см + 4 мм 18 см = 1 дм + 8 см 10 ц – 20 кг > 100 кг 90 дм > 1 м – 20 см 400 мм + 600 мм = 1 м 400 г + 100 г < 5 кг	70 см + 4 мм = 700 мм + 4 мм = 704 мм, 704 мм > 4 мм 1 дм + 8 см = 10 см + 8 см = 18 см, 18 см = 18 см 10 ц – 20 кг = 1000 кг – 20 кг = 980 кг, 980 кг > 100 кг 1 м – 20 см = 10 дм – 2 дм = 8 дм, 90 дм > 8 дм 400 м + 600 мм = 1000 мм = 1 м, 1 м = 1 м 400 г + 100 г = 500 г, 500 г < 5 кг

Завдання 712

Два велосипедисти рухалися назустріч один одному. Швидкість першого велосипедиста становить 15 км/год, а швидкість другого — 16 км/год. На скільки кілометрів велосипедисти наблизяться один до одного через 2 год?

Схематичний рисунок.

15 км/год —>                        t = 2 год               <— 16 км/год        |——————————————∆———————————|  I велосипедист                     S = ? км                II велосипедист

Розв'язання

1–ий спосіб

1) 15 • 2 = 30 (км) – відстань проїхав перший велосипедист через 2 год;

2) 16 • 2 = 32 (км) – відстань проїхав другий велосипедист через 2 год.

3) 30 + 32 = 62 (км)

2–ий спосіб

1) 15 + 16 = 31 (км) – на таку відстань наблизяться через 1 год;

2) 31 • 2 = 62 (км) – на таку відстань наблизяться через 2 год.

Відповідь: на 62 км велосипедисти наблизяться один до одного через 2 год.

 

Завдання 713

З пункту А в протилежних напрямках виїхали два моторолери. Швидкість руху першого — 50 км/год, а другого — 40 км/год. Через скільки годин відстань між ними становитиме 180 км?

Схематичний рисунок.

t = ? год                               <— 50 км/год       40 км/год —>         |—————————————∆————————————| 1—ий моторолер                S = 180 км            2—ий моторолер

Розв'язання

1) 50 + 40 = 90 (км/год) – швидкість віддалення.

2) 180 : 90 = 2 (год)

Відповідь: через 2 год відстань між ними становитиме 180 км.

 

Завдання 714

Сад має форму прямокутника. Довжина саду дорівнює 12 м, а ширина вдвічі менша. Обчисли довжину паркану навколо саду.

Короткий запис

Довжина – 12 м

Ширина – ?,  у 2 р. менша, ніж довжина

Р – ?

Розв'язання

1) 12 : 2 = 6 (м) – ширина прямокутного паркану;

2) (12 + 6) • 2 = 18 • 2 = 36 (м) – довжина прямокутного паркану.

Відповідь: довжина паркану навколо саду 36 м.

 

ДЛЯ ТИХ, ХТО НЕ БОЇТЬСЯ ТРУДНОЩІВ

Завдання 715 Розшифруй ребуси.

ПАРОСТОК ІСТОРІЯ

ТРИВОГА

Завдання 716

Запиши число, яке можна поділити на будь–яке інше число, але не можна поділити саме на себе. 0 (На нуль ділити не можна!)

 

Завдання 717

Назви всі числа, які «заховалися» за фруктами. Обчисли результат.

х – одне яблуко х + х + х = 300 3х = 300 х = 300 : 3 х = 100 – одне яблуко 100 + 100 + 100 = 300	х – один банан 100 + 2х = 180 2х = 180 – 100 2х = 80 х = 80 : 2 х = 40 – один банан 100 + 40 + 40 = 180
х – один кокос 40 – 2х = 20 2х = 40 – 20 2х = 20 х = 20 : 2 х = 10 – один кокос 40 – 10 – 10 = 20	10 + 100 + 40 = 150

Завдання 718

У родині 2 батьки, 2 сини, дідусь та онук. Батькам разом 80 років, синам — 40 років, а дідусеві та онукові разом

60 років. Скільки років разом усім чоловікам?

Дідусь – батько

Син дідуся – син, батько

Онук – син

Розв'язання

Якщо двом батькам (дідусь та син дідуся) 80 років, двом синам (син дідуся і внук) 40 років, а дідусеві й онуку 60 років, тоді

1) 80 + 40 – 60 = 60 (р.) – подвоєний вік сина дідуся;

2) 60 : 2 = 30 (р.) – вік синові дідуся;

3) 80 – 30 = 50 (р.) – вік дідуся;

4) 60 – 50 = 10 (р.) – вік онука.

5) 30 + 50 + 10 = 90 (р.)

Відповідь: усім чоловікам родини разом 90 років.

 

Завдання 719

Радіус круга дорівнює 6 см. Чи поміститься в середині цього круга відрізок завдовжки 10 см? (Підказка: знайди діаметр круга.)

Розв'язання

1) 6 • 2 = 12 см – діаметр круга.

12 см > 10 см

Відповідь: поміститься.

 

Завдання 720

Від свого будинку Микола проїхав на велосипеді в одному напрямку 800 м, а потім у протилежному напрямку — 1090 м. Скільки всього метрів проїхав Микола? На якій відстані від свого будинку він опинився?

Короткий запис

Відстань вперед — 800 м

Відстань назад — 1099 м

Загальна відстань — ?

Відстань від свого будинку — ?

Розв'язання

1) 800 + 1090 = 1890 (м) – загальна відстань, яку проїхав Микола;

2) 1090 – 800 = 290 (м) – відстань від свого будинку.

Відповідь: Микола проїхав всього 1890 м, опинився на відстані 290 м від свого будинку.

 

Завдання 721

Сума всіх чисел від 1 до 100 дорівнює 5050. Обчисли зручним способом.

(1 + 99) + (2 + 98) + (3 + 97) + ... + (48 + 52) + (49 + 51) + 50 = 50 • 100 + 50 = 5050

 

Завдання 722

Виконай обчислення та доведи, що під час множення «чисел–перевертнів» рівність зберігається.

13 • 93 = 31 • 39 1209 = 1209

х 13    93    39  117   1209

х 31    39   279   93   1209

14 • 82 = 41 • 28 1148 = 1148

х 14    82    28  112   1148

х 41    28   328   82    1148

Завдання 723

Швидкість скутера дорівнює 10 м/с, а швидкість вітру — 4 м/с. Визнач швидкість руху скутера за вітром і проти вітру.

Короткий запис

Швидкість скутера — 10 м/с

Швидкість вітру — 4 м/с

Швидкість руху за вітром — ?

Швидкість руху проти вітра — ?

Розв'язання

1) 10 + 4 = 14 (м/с) – швидкість руху за вітром;

2) 10 – 4 = 6 (м/с) – швидкість руху проти вітру.

Відповідь: 14 м/с і 6 м/с.

 

Завдання 724

Скільки часу необхідно штучному супутникові Землі, щоб пролетіти 180 000 км, якщо його швидкість становить 10 км/с?

Короткий запис

Відстань – 180 000 км

Швидкість – 10 км/с

Час – ?

Розв'язання

1) 180 000 : 10 = 18 000 (с)

2) 18 000 с : 60 = 300 хв

3) 300 хв : 60 = 5 год

Відповідь: штучному супутникові Землі потрібно 18 000 секунд, або 300 хв, або 5 год.

 

Завдання 725

З одного річкового порту до іншого одночасно вирушили в одному напрямку пароплав і катер. Швидкість пароплава дорівнює 34 км/год, а швидкість катера — 48 км/год. Яка відстань буде між ними через 6 год після початку руху?

Схематичний рисунок: 

пароплав                         t = 6 год , s — ?     ———> 34 км год                          ∆———————————————————————————|     —————>  48 км/год  катер

Розв'язання

1–ий спосіб

1) 48 – 34 = 14 (км) – на таку відстань віддаляться через 1 год;

2) 14 • 6 = 84 (км) – на таку відстань віддаляться через 6 год.

2–ий спосіб

1) 48 • 6 = 288 (км) – відстань пройшов катер через 6 год;

2) 34 • 6 = 204 (км) – відстань пройшов пароплав через 6 год.

3) 288 – 204 = 84 (км)

Відповідь: через 6 год відстань між ними буде 84 км.

 

Завдання 726

У старому млині мешкали павуки й стоніжки. Усього було 540 ніг і 10 голів. Скільки павуків і скільки стоніжок мешкало в старому млині?

 

Завдання 728 Завдання від героїв мультфільму «Фіксики».

Щоб усно помножити число на 8, потрібно до першого множника дописати нуль і відняти подвоєний множник.

27 • 8 = 27 • 10 – (27 • 2) = 270 – 54 = 216

36 • 8 = 360 – 72 = 288

Щоб усно помножити число на 9, потрібно дописати до нього нуль і відняти множник.

48 • 9 = 48 • 10 – 48 = 480 – 48 = 432

64 • 9 = 640 – 64 = 576

73 • 9 = 730 – 73 = 657

Округлення одного з компонентів під час додавання чи віднімання.

597 + 138 = (597 + 3 + 138) – 3 = 600 + 135 = 735

475 – 298 = 475 – (298 + 2) + 2 = 475 – 300 + 2 = 177

 

Завдання 729 

Назвіть одиниці вимірювання довжини, якими ви користуєтеся.

Назвіть давні одиниці вимірювання довжини, якими користувалися колись.

Інші завдання дивись тут...