ГДЗ Математика 4 клас Оляницька Завдання 138 – 167 Відповіді

Інші завдання дивись тут...

ПЕРЕВІРЯЄМО СВОЇ ДОСЯГНЕННЯ

Завдання 138

Суму розрядних доданків 800 + 30 + 1 записано числом

В 831

800 + 30 + 1 = 831

Завдання 139

Різниця двох чисел дорівнює 74. Від’ємник дорівнює 26, зменшуване дорівнює

Б 100

Нехай зменшуване дорівнює х. Складаємо рівняння і розв'язуємо:

х – 26 = 74

х = 74 + 26

х = 100

Завдання 140

Добуток чисел 17 і 4 дорівнює

А 68

17 • 4 = (10 + 7) • 4 = 40 + 28 = 68

Завдання 141

Частка чисел 219 і 3 дорівнює

В 97

219 : 3 = (210 + 9) • 3 = 70 + 27 = 97

Завдання 142

6 год — це

Б 360 хв

1 год = 60 хв, 60 хв • 6 = 360 хв

Завдання 143 Порядок дій

720 : 8 + 28 • 5 = 720 : 8 + (20 + 8) • 5 = 90 + 100 + 40 = 230

800 – (34 + 19) • 4 = 800 – 53 • 4 = 800 – (50 + 3) • 4 = = 800 – (200 + 12) =

= 600 – 12 = 588

310 • 3 – 45 • 0 = (300 + 10) • 3 – 45 • 0 = 900 + 30 – 0 = 930

Завдання 144 Письмове додавання і письмове віднімання

+ 489

372

861

_ 904

386

518

+318

593

911

_1000

581

419

Завдання 145 Порівняй іменовані числа (>; <; = )

900 г < 3 кг (3 кг = 3000 г, 900 г < 300 г)

3 ст. > 100 р. (3 ст. = 3000 р., 3000 р. > 100 р.)

4 дм < 60 см (4 дм = 40 см, 40 см < 60 см)

350 кг < 1 т (1 т = 1000 кг, 350 кг < 1000 кг)

48 год = 2 доби (2 доби = 48 год, 48 год = 48 год)

100 мм < 1 км (1 км = 1000 м, 100 мм < 1000 м)

Завдання 146 Ділення з остачею

17 : 3 = 5 (ост. 2)

58 : 8 = 7 (ост. 2)

107 : 10 = 10 (ост. 7)

801 : 100 = 8 (ост. 1)

Завдання 147

Сторона першого квадрата дорівнює 8 см, другого — на 3 см довша. На скільки сантиметрів периметр другого квадрата більший за периметр першого?

^{Короткий запис}

^{Сторона I кв. — 8 см}

^{Сторона II кв. — ?, на 3 см більше}

^{Периметр I кв. — ?}

^{Периметр II кв. — ? На скільки більший — ?}

Розв’язання

1) 8 + 3 = 11 (см) – сторона II квадрата;

2) 8 • 4 = 32 (см) – периметр I квадрата;

3) 11 • 4 = 44 (см) – периметр II квадрата.

4) 44 – 32 = 12 (см)

Відповідь: на 12 см периметр другого квадрата більший.

Завдання 148

Перший майстер працював 5 год, а другий — 4 год. Скільки іграшок виготовив кожен майстер окремо, працюючи з однаковою продуктивністю праці, якщо разом вони виготовили 189 іграшок?

	^{Продуктивність праці}	^{Час виконання}	^{Кількість іграшок}
^{I майстер}	^{?, однакова}	^{5 год}	^?	^{189 ігр.}
^{II майстер}	^{?, однакова}	^{4 год}	^?	^{189 ігр.}

Розв’язання

1) 5 + 4 = 9 (год) – весь час;

2) 189 : 9 = 21 (ігр.) – виготовляє кожний майстер за 1 год;

3) 21 • 5 = (20 + 1) • 5 = 100 + 5 = 105 (ігр.) – виготовив I майстер;

4) 21 • 4 = (20 + 1) • 4 = 80 + 4 = 84 (ігр.) – виготовив II майстер.

Відповідь: перший майстер виготовив 105 ігор, другий майстер — 84 ігор.

Завдання 149

5 термометрів показують 20 градусів тепла. Яку температуру показуватиме один термометр? 20 градусів.

§ 16 Завдання 150

Обчисліть «ланцюжок» виразів і дізнаєтеся висоту (у метрах) монумента Батьківщина–мати, розташованого в Києві на березі Дніпра.

20 • 5 • 4 : 5 • 10 • 5 : 25 – 58 = 160 – 58 = 102 (м)

Висота статуї від п’єдесталу до вістря меча — 62 м. Скористайтеся попередніми обчисленнями й визначте висоту п’єдесталу.

102 – 62 = 40 (м)

Завдання 151 Множення чисел

43 • 2 = (40 + 3) • 2 = 40 • 2 + 3 • 2 = 80 + 6 = 86

Завдання 152, 153

х 43

х 32

х 22

х 33

х 42

Завдання 154

У касі зоопарку до обіду продали 23 квитки, а після обіду — у 3 рази більше. Скільки квитків продали в касі зоопарку за весь день?

^{Короткий запис}

^{До обіду — 23 кв.}

^{Після обіду — ?, у 3 рази більше}

^{За день — ?}

Розв’язання

1) 23 • 3 = 69 (кв.) – продали після обіду.

2) 23 + 69 = 92 (кв.)

Відповідь: за весь день продали 92 квитки.

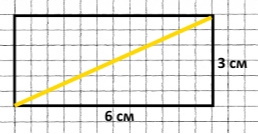
Завдання 155 Практична робота

Побудуй прямокутник зі сторонами 6 см і 3 см. Проведи в ньому відрізок, який з’єднає протилежні вершини прямокутника. Виміряй довжину цього відрізка.

Відрізок поділив прямокутник на два рівні трикутники.

Довжина цього відрізка 6 см 7 мм.

6 см + 3 см + 6 см 7 мм = 15 см 7 мм – периметр кожного утвореного трикутника.

Завдання 156

Діти отримали завдання накреслити 5 відрізків. Перший відрізок завдовжки 2 см, а кожний наступний у 2 рази довший за попередній. Яка довжина п’ятого відрізка?

^{Короткий запис}

^{I — 2 cм}

^{II — ?, у 2 рази більше, ніж I}

^{III — ?, у 2 рази більше, ніж II}

^{IV — ?, у 2 рази більше, ніж III}

^{V — ?, у 2 рази більше, ніж IV}

Розв’язання

1) 2 • 2 = 4 (см) – довжина II відрізка;

2) 4 • 2 = 8 (см) – довжина III відрізка;

3) 8 • 2 = 16 (см) – довжина IV відрізка;

4) 16 • 2 = 32 (см) – довжина V відрізка.

Відповідь: довжина п'ятого відрізка 32 сантиметрів.

Завдання 157

х 23

х 32

х 34

х 41

Завдання 158

Бригада робітників першого дня відремонтувала 12 м дороги, а другого — у 4 рази більше. Скільки метрів дороги відремонтувала бригада за 2 дні?

^{Короткий запис}

^{I — 12 м}

^{II — ?, у 4 рази більше}

^{Разом — ?}

Розв’язання

1) 12 • 4 = 48 (м) – відремонтували за II день.

2) 12 + 48 = 60 (м)

Відповідь: бригада відремонтувала 60 метрів дороги.

§ 17 Завдання 159

Обчисліть «ланцюжок» виразів і дізнаєтеся довжину (у кілометрах) Оптимістичної печери — найдовшої гіпсової печери на Землі, яка знаходиться в Тернопільській області.

60 • 3 : 9 • 7 : 2 • 3 + 80 – 30 = 210 + 80 – 30 = 260 (км)

Завдання 160

х 36

Завдання 161

42 • 3 = (40 + 2) • 3 = 40 • 3 + 2 • 3 = 120 + 6 = 126

54 • 3 = (50 + 4) • 3 = 50 • 3 + 4 • 3 = 150 + 12 = 172

Завдання 162

х 27

х 28

х 62

372

х 33