ГДЗ Математика 4 клас Оляницька Завдання 195 – 221 Відповіді

Інші завдання дивись тут...

§ 21 Завдання 195

Назвіть трикутники, у яких є прямий кут. KDF, SOT

Як це можна перевірити? Вимірюванням

Завдання 196 Письмове множення

х 74

518

х 165

660

х 304

912

х 118

590

Завдання 197 Запиши кілька значень змінних, за яких нерівності істинні.

2 • а < 30,

яa = 0, 1, 2

36 : c > 4,

с = 1, 2, 3

d : 6 < 7,

d = 6, 12, 18

11 • b > 34,

b = 4, 5, 6

Завдання 198 Порядок дій

175 • 3 + 560 : 7 – (48 • 4 – 135) = 548
х 48 4 192	_ 192 135 57	х 175 3 525	_560 \| 7 56 80 0	+ 525 80 605	_ 605 57 548

Завдання 199

За 1 год бабуся прополола 9 рядків картоплі, а тато — на 3 рядки більше. Скільки рядків картоплі прополють тато й бабуся разом за 2 години?

План розв’язування задачі:

1) Скільки рядків картоплі прополить тато за 1 годину?

2) Скільки рядків картоплі тато й бабуся разом прополять за 1 годину?

3) Скільки рядків картоплі тато й бабуся разом прополять за 2 години?

Розв’яжи задачу.

^{Короткий запис}

^{Бабуся — 1 год — 9 р.}

^{Тато — 1 год — ?, на 3 р. більше}

^{Разом — 2 год — ? р.}

Розв’язання

1) 9 + 3 = 12 (р.) – прополить тато за 1 год;

2) 9 + 12 = 21 (р.) – прополють тато з бабусею разом за 1 год;

3) 21 • 2 = 42 (р.) – прополють тато з бабусею разом за 2 год.

Відповідь: тато й бабуся разом прополють 42 рядки картоплі.

Завдання 200

Перша бригада будівельників за 4 год проклала 24 м труб, а друга бригада за 1 год — на 1 м більше, ніж перша бригада за 1 год. За скільки годин обидві бригади прокладуть 130 м труб, працюючи разом?

^{Короткий запис}

^{I — 4 год — 24 м}

^{I — 1 год — ?}

^{II — 1 год — ?, на 1 м більше}

^{Разом — ? год — 130 м}

Розв’язання

1) 24 : 4 = 6 (м) – труби проклала I бригада за 1 год;

2) 6 + 1 = 7 (м) – труби проклала II бригада за 1 год;

3) 6 + 7 = 13 (м) – труби проклали обидві бригади за 1 год.

4) 130 : 13 = 10 (год)

Відповідь: за 10 годин обидві бригади прокладуть 130 м труб, працюючи разом.

Завдання 201

Розглянь малюнок і визнач, скільки лимонів потрібно взяти, щоб зрівноважити одну диню.

^{Короткий запис}

^{3 яблука + 1 диня = 10 яблук}

^{1 диня = 6 лимонів + 1 яблуко}

^{1 диня = ? лимонів}

Розв'язання

1 диня = 10 яблук – 3 яблука

1 диня = 7 яблук

7 яблук = 6 лимонів + 1 яблуко

7 яблук – 1 яблуко = 6 лимонів

6 яблук = 6 лимонів

1 яблуко = 1 лимону, отже, 1 диня = 7 лимонів.

Відповідь: одну диню зрівноважать 7 лимонів.

Завдання 202

х 93

744

х 387

774

х 108

756

х 217

651

Завдання 203

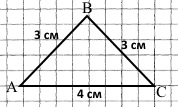
Побудуй у зошиті довільний трикутник. Обчисли його периметр.

Розв’язання

3 + 3 + 4 = 10 (см)

Відповідь: периметр трикутника 10 сантиметрів.

§ 22 Завдання 204

Обчисліть «ланцюжок» виразів і дізнаєтеся, скільки в Єгипті найвідоміших великих пірамід. Назвіть якомога більше дільників цього числа.

(9 • 100 – 300) : 10 • 9 : 10 : 6 • 1 = 9

Дільники числа 9: 1, 3, 9

1) 9 • 100 = 900

2) 900 – 300 = 600

3) 600 : 10 = 60

4) 60 • 9 = 540

5) 540 : 10 = 54

6) 54 : 6 = 9

7) 9 • 1 = 9

Завдання 205

Піраміди: 1, 3, 4

З’ясуй, з яких плоских фігур складається піраміда: трикутників і прямокутника.

Завдання 206

23 • 4 = (20 + 3) • 4 = 20 • 4 + 3 • 4 = 80 + 12 = 92

92 : 23 = 4

92 : 4 = 23

11 • 8 = (10 + 1) • 8 = 10 • 8 + 1 • 8 = 80 + 8 = 88

88 : 11 = 8

88 : 8 = 11

12 • 8 = (10 + 2) • 8 = 10 • 8 + 2 • 8 = 80 + 16 = 96

96 : 12 = 8

96 : 8 = 12

Завдання 207 Ділення чисел

28 : 2 = (20 + 8) : 2 = 20 : 2 + 8 : 2 = 10 + 4 = 14

72 : 6 = (60 + 12) : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12

Завдання 208, 209 Письмове ділення

_48 | 4

4 12

_84 | 4

8 21

_96 | 3

9 32

_55 | 5

5 11

_68 | 2

6 34

Завдання 210

У череді було 36 корів, а телят — у 3 рази менше. Скільки всього тварин було в цій череді?

^{Короткий запис}

^{Корів — 36 тв.}

^{Телят — ?, у 3 рази менше}

^{Разом — ?}

Розв’язання

1) 36 : 3 = 12 (тв.) – телят в череді;

2) 36 + 12 = 48 (тв.) – корів і телят в череді.

Відповідь: у цій череді було 48 тварин.

Завдання 211

_64 | 2

6 32

_93 | 3

9 31

_88 | 4

8 22

_82 | 2

8 41

Завдання 212

У саду росло 69 фруктових дерев. Третю частину всіх дерев становили груші, а решту — яблуні. Скільки яблунь росло в саду?

^{Короткий запис}

^{Усього — 69 д.}

^{Груші — ?, у 3 рази менше}

^{Яблуні — ?, решта}

Розв’язання

1) 69 : 3 = 23 (д.) – росло груш;

2) 69 – 23 = 46 (д.) – решта, або росло яблунь.

Відповідь: в саду росло 46 яблунь.

§ 23 Завдання 213 Усього одиниць даного розряду містить число

У числі 281 — 28 дес.

У числі 610 — 61 дес.

У числі 603 — 60 дес.

У числі 182 — 18 дес.

У числі 930 — 93 дес.

У числі 100 — 10 дес.

Завдання 214

684 : 2 = (600 + 80 + 4) : 2 = 600 : 2 + 80 : 2 + 4 : 2 = 300 + 40 + 2 = 342

276 : 3 = (270 + 6) : 3 = 270 : 3 + 6 : 3 = 90 + 2 = 92

Завдання 215, 216

_624 | 2

6 312

_848 | 4

8 212

_966 | 3

9 322

_486 | 2

4 243

Завдання 217

Два ряди обласного стадіону мають 448 місць, а один ряд стадіону в райцентрі — у 2 рази менше місць, ніж один ряд обласного стадіону. Скільки місць в одному ряду стадіону в райцентрі?

^{Короткий запис}

^{У області — 2 р. — 448 м.}

^{У області — 1 р. — ?}

^{У райцентрі — 1 р. — ?, у 2 рази менше}

Розв’язання

1) 448 : 2 = 224 (м.) – у ряді обласного стадіону;

2) 224 : 2 = 112 (м.) – у ряді стадіону в райцентрі.

Відповідь: в одному ряду стадіону в райцентрі 112 місць.

_448| 2

4 224

_224| 2

2 112

Завдання 218

За 1 год нові серії мультфільму «Фіксики» у ютубі переглянули 864 користувачі. Це у 2 рази більше тих, хто переглянув за 1 год старі серії. Скільки користувачів переглянули за 1 год старі серії мультфільму «Фіксики»?

^{Короткий запис}

^{Нові — 864 к., це у 2 рази більше}

^{Старі — ?}

Розв’язання

_864 | 2

8 432 (к.)

Відповідь: старі серії мультфільму переглянули 432 користувачі.

Завдання 219 Рівняння

у • 4 = 848 у = 848 : 4 у = 212	х : 5 = 102 х = 102 • 5 х = 510	3 • z = 639 z = 639 : 3 z = 213
_848 \| 4 8 212 _4 4 _8 8 0	х 102 5 510	_639 \| 3 6 213 _3 3 _9 9 0