ГДЗ математика 5 клас Істер вправи 1183 – 1215 § 37 Мішані числа ВІДПОВІДІ до підручника

Завдання 1183

Сім цілих дві третіх, п'ять цілих дві одинадцятих, сто сімнадцять цілих дванадцять тринадцятих, десять цілих двадцять одна сто других.

Завдання 1184 Додавання дробів

1) 5 + 1/6 = 5 1/6

2) 7 + 3/4 = 7 3/4

3) 3/7 + 19 = 19 3/7

4) 4/9 + 15 = 15 4/9

Завдання 1185

1) 9 + 1/3 = 9 1/3

2) 7 + 2/5 = 7 2/5

3) 1/9 + 4 = 4 1/9

4) 17/19 + 23 = 23 17/19

Завдання 1186

1) 7 1/8 = 7 + 1/8

2) 3 4/5 = 3 + 4/5

3) 5 1/17 = 5 + 1/17

4) 14 13/18 = 4 + 13/18

Завдання 1187

1) 13 1/9 = 13 + 1/9

2) 5 3/7 = 5 + 3/7

3) 12 135/136 = 12 + 135/136

4) 2022 1/2023 = 2022 + 1/2023

Завдання 1188

Числа, у яких ціла частина дорівнює нулю: 1/2, 5/6, 7/10 — це дробові числа.

Завдання 1189

Числа, у яких дробова частина дорівнює нулю. 1, 5, 60 — це натуральні числа.

Завдання 1190 Перетворення дробів

1) 21/5 = 4 1/5

5) 142/13 = 10 12/13

2) 311/100 = 3 11/100

6) 512/10 = 51 2/10

3) 36/3 = 12

7) 2569/11 = 233 6/11

4) 125/7 = 17 6/7

8) 552/8 = 69

Завдання 1191

1) 118/3 = 39 1/3

5) 319/100 = 3 19/100

2) 49/10 = 4 9/10

6) 275/25 = 11

3) 116/4 = 29

7) 1189/7 = 169 6/7

4) 257/8 = 32 1/8

8) 1147/25 = 45 22/25

Завдання 1192

1) 19 : 2 = 19/2 = 9 1/2

2) 26 : 5 = 26/5 = 5 1/5

3) 57 : 10 = 57/10 = 5 7/10

4) 62 : 25 = 62/25 = 2 12/25

Завдання 1193

1) 27 : 2 = 27/2 = 13 1/2

2) 147 : 5 = 29 2/5

3) 313 : 13 = 24 1/13

4) 3189 : 1000 = 3189/1000 = 3 189/1000

Завдання 1194 Порівняння дробів

1) 7 2/5 > 7

3) 7 8/11 < 8 9/100

2) 4 5/9 < 5

4) 17 2/5 > 17 1/5

Завдання 1195

1) 5 1/7 < 6

2) 9 2/3 > 9

3) 5 10/11 < 6 2/3

4) 8 5/9 > 8 4/9

Завдання 1196

Накресли координатний промінь, узявши за одиничний відрізок 5 клітинок. Познач на ньому неправильні дроби 7/5 , 13/5 , 9/5 , 11/5 , 14/5 , попередньо виділивши цілу та дробову частини кожного з них.

7/5 = 1 2/5

13/5 = 2 3/5

9/5 = 1 4/5

11/5 = 2 1/5

14/5 = 2 4/5

Завдання 1197

1) 8 км 113 м = 8 113/1000 км

3 км 8 м = 3 8/1000 км

2) 3 год 19 хв = 3 19/60 год

7 год 1 хв = 7 1/60 год

Завдання 1198

1) 9 > 17/2 (17/2 = 8 1/2)

2) 18/3 = 6; (18/3 = 6)

3) 18/6 < 16/5 (18/6 = 3, 16/5 = 3 1/5)

4) 32/9 < 14/3 (32/9 = 3 5/9, 14/3 = 4 2/3)

Завдання 1199

1) 17/3 < 6

2) 8 < 25/3

Завдання 1200

47/5 = 9 2/5 43/4 = 10 3/4	73/9 = 8 1/9 41/4 = 10 1/4	35/3 = 11 2/3 72/8 = 9
У порядку зростання: 73/9 Д 72/8 О 47/5 Л 41/4 И 43/4 Н 35/3 А Місто: ДОЛИНА

Завдання 1201

25/3 = 8 1/3	252/36 = 7	73/8 = 9 1/8	132/13 = 10 2/13	37/5 = 7 2/5
У порядку зростання: 252/36, 37/5, 25/3, 73/8, 132/13

Завдання 1202

47/9 > n правильна при n = 1, 2, 3, 4, 5, бо 47/9 = 5 2/9

Завдання 1203

m > 37/6 правильна при найменшому m = 7, бо 37/6 = 6 1/6

Завдання 1204

k < 37/8 була правильна при найбільшому k = 4, бо 37/8 = 4 5/8

Завдання 1205

Три числа, які більші за 7, але менші від 8: 7 1/2, 7 2/4, 7 50/100

Завдання 1206

Турист подолав 19 км за 4 год. З якою швидкістю він рухався?

Розв'язання

19 : 4 = 19/4 = 4 3/4 (км/год) – швидкість туриста.

Відповідь: 4 3/4 км/год.

Завдання 1207

Карлсон спустошив 9 баночок варення за 32 хв. За скільки хвилин він спустошує 1 таку баночку?

Розв'язання

32 : 9 = 32/9 = 3 5/9 (хв) – спустошує 1 баночку.

Відповідь: 3 5/9 хв.

Завдання 1208

На пошиття 15 однакових костюмів майстерня витратила 32 м тканини. Чи вистачає 2 м тканини на пошиття одного такого костюма?

Розв'язання

32 : 15 = 32/15 = 2 2/15 (м) – потрібно на пошиття 1 костюма.

2 < 2 2/15

Відповідь: не вистачає.

Завдання 1209

Мавпочка Абу розфасувала 41 кг бананів у 5 однакових ящиків. Чи поміщається в один такий ящик 8 кг бананів?

Розв'язання

41 : 5 = 41/5 = 8 1/5 (кг) – маса одного такого ящика.

8 < 8 1/5

Відповідь: поміщається.

Завдання 1210

Перше фермерське господарство з площі 80 м² зібрало 6 ц моркви, друге з 90 м² — 6 ц 20 кг, а третє зі 100 м² — 8 ц. У якого з господарств (у кг з 1 м²) урожайність найбільша? У якого — найменша?

Розв'язання

1) 600 : 80 = 600/80 = 7 40/80 (кг) – з першого господарства.

2) 620 : 90 = 620/90 = 6 80/90 (кг) – з другого господарства.

2) 800 : 100 = 8 (кг) – з третього господарства.

Відповідь: найбільша урожайність з третього господарства, а найменша — з другого.

Завдання 1211

5 2/7 < a/7 < 6 4/7 , 37/7 < a/7 < 46/7, при трьох значеннях а = 38, 39, 40.

Завдання 1212

1) найбільший правильний дріб зі знаменником 17: 16/17

2) найменший неправильний дріб із чисельником 20: 20/20

Завдання 1213 Якими цифрами можна замінити «зірочку», щоб дріб:

1) 7*5/775 буде неправильний: 785/775, 795/775

2) 783/7*4 буде правильний: 783/794

Завдання 1214 Ділення з остачею

До встановлення лічильників родина Петренків платила за користування водою 590 грн щомісяця. Після встановлення двох лічильників (на холодну та гарячу воду) щомісячна сплата за воду стала складати 360 грн. Один лічильник води коштував 390 грн, а його встановлення — 150 грн. Через яку найменшу кількість місяців економія з оплати води перевищить витрати на купівлю та установку лічильників, якщо тарифи на воду не зміняться?

Розв'язання

1) 590 – 360 = 230 (грн) – економія щомісяця.

2) (390 + 150) • 2 = 1080 (грн) – витратила на лічильники.

3) 1080 : 230 = 4 (ост. 160) (м.)

Відповідь: щонайменше через 5 місяців економія з оплати води перевищить витрати на купівлю та установку лічильників.

Завдання 1215

Прямокутник зі сторонами 2 см і 6 см розрізали на два рівних між собою прямокутники. Знайди периметр кожного з них.

Розв'язання

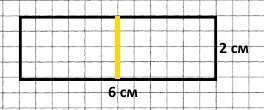
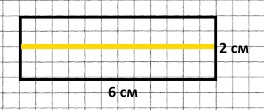
випадок 1:	випадок 2:

1) 6 : 2 = 3 (см) – довжина прямокутника. 2) (2 + 3) • 2 = 10 (см) Відповідь: 10 см.	1) 2 : 2 = 1 (см) – ширина прямокутника. 2) (6 + 1) • 2 = 14 см) Відповідь: 14 см.