Завдання 1807
Карлсон і Малюк разом з’їли 3,6 кг варення, причому Карлсон з’їв утричі більше, ніж Малюк. Скільки варення з’їв Карлсон і скільки — Малюк?
Розв’язання
1 спосіб
Нехай Малюк з'їв х кг варення, тоді Карлсон з"їв 3х кг. Разом вони з'їли 3,6 кг варення. Складаємо рівняння:
х + 3х = 3,6
4х = 3,6
х = 3,6 : 4
х = 0,9 (кг) – варення з'їв Малюк;
0,9 • 3 = 2,7 (кг) – варення з'їв Карлсон.
2 спосіб
1) 1 + 3 = 4 (ч.) – всього частин;
2) 3,6 : 4 = 0,9 (кг) – варення з'їв Малюк;
3) 0,9 • 3 = 2,7 (кг) – – варення з'їв Карлсон.
3 спосіб
1) 1 + 3 = 4 (ч.) – всього частин;
2) 3,6 : 4 = 0,9 (кг) – варення з'їв Малюк;
3) 3,6 – 0,9 = 2,7 (кг) – – варення з'їв Карлсон.
Відповідь: 2,7 кг; 0,9 кг.
Завдання 1808
Вантаж масою 4,8 т розмістили на двох вантажівках, причому на першій — на 0,6 т більше, ніж на другій. Скільки т вантажу було на кожній вантажівці?
Розв’язання
1 спосіб
Нехай на другій вантажівці розмістили х т вантажу, тоді на першій розмістили (х + 0,6) т. Складаємо рівняння:
(х + 0,6) + х = 4,8
2х + 0,6 = 4,8
2х = 4,8 – 0,6
2х = 4,2
х = 4,2 : 2
х = 2,1 (т) – вантажу розмістили на другій вантажівці;
2,1 + 0,6 = 2,7 (т) – вантажу розмістили на першій вантажівці.
2 спосіб
Нехай на першій вантажівці розмістили х т вантажу, тоді на другій розмістили (х – 0,6) т. Складаємо рівняння:
х + (х – 0,6) = 4,8
х + х – 0,6 = 4,8
2х – 0,6 = 4,8
2х = 4,8 + 0,6
2х = 5,4
х = 5,4 : 2
х = 2,7 (т) – вантажу розмістили на першій вантажівці;
2,7 – 0,6 = 2,1 (т) – вантажу розмістили на другій вантажівці.
Відповідь: 2,7 т; 2,1 т.
Завдання 1809
Робітники, працюючи втрьох, за 7 год виготовили 1001 деталь. Причому перший виготовив 3/11 усіх деталей, а другий — 5/13 усіх деталей. Скільки деталей за годину виготовляв третій робітник?
|
Розв’язання
1) 1001 : 11 • 3 = 91 • 3 = 273 (д.) — виготовив I робітник;
2) 1001 : 13 • 5 = 77 • 5 = 385 (д.) — виготовив II робітник;
3) 273 + 385 = 658 (д.) — виготовили I і II робітники разом;
4) 1001 – 658 = 343 (д.) — виготовив III робітник за 7 год;
5) 343 : 7 = 49 (д.) — виготовляв III робітник за 1 год.
Відповідь: 49 деталей.
|
||||||
|
_1001| 11 99 91 _11 11 0 |
х 91
3
273
|
_1001| 13 91 77 _91 91 0 |
х 77 5 385 |
+273 385 658 |
_1001 658 343 |
_343| 7 28 49 _63 63 0 |
Завдання 1810 Ознайомлення з дробами
Від деякого числа відняли його 1/10 та отримали 14,4. Знайди це число.
Розв’язання
1 спосіб
Нехай шукане число дорівнює х, тоді 1/10 (або 0,1) цього числа дорівнює 0,1х. Складаємо рівняння.
х – 0,1х = 14,4
0,9х = 14,4
х = 14,4 : 0,9
х = 16
2 спосіб
1) 1 – 1/10 = 10/10 – 1/10 = 9/10 – припадає на 14,4;
2) 14,4 : 9 • 10 = 1,6 • 10 = 16 – шукане число.
Відповідь: 16.
Завдання 1811
До деякого числа додали його 1/5 і отримали 74,4. Знайди це число.
Розв’язання
1 спосіб
Нехай шукане число дорівнює х, тоді 1/5 (або 0,2) цього числа дорівнює 0,2х. Складаємо рівняння.
х + 0,2х = 74,4
1,2х = 74,4
х = 74,4 : 1,2
х = 62
2 спосіб
1) 1 + 1/5 = 5/5 + 1/5 = 6/5 – припадає на 74,4;
2) 74,4 : 6 • 5 = 12,4 • 5 = 62 – шукане число.
Відповідь: 62.
Завдання 1812
Знайди два числа, сума яких — 4,7, а різниця — 3,1.
Розв’язання
1 спосіб
Нехай друге число дорівнює х, за умовою різниця цих чисел дорівнює 3,1, тому перше число дорівнює (х + 3,1), а сума цих чисел дорівнює 4,7. Складаємо рівняння.
х + (х + 3,1) = 4,7
2х + 3,1 = 4,7
2х = 4,7 – 3,1
2х = 1,6
х = 1,6 : 2
х = 0,8 – друге число;
0,8 + 3,1 = 3,9 – перше число.
2 спосіб
Нехай перше число дорівнює х, за умовою сума цих чисел дорівнює 4,7, тому друге число дорівнює (4,7 – х), а різниця цих двох чисел дорівнює 3,1. Складаємо рівняння.
х – (4,7 – х) = 3,1
х – 4,7 + х = 3,1
2х – 4,7 = 3,1
2х = 3,1 + 4,7
2х = 7,8
х = 7,8 : 2
х = 3,9 – друге число;
4,7 – 3,9 = 0,8 – друге число.
Відповідь: 3,9; 0,8.
Завдання 1813
Сума двох чисел дорівнює 27,2. Знайди ці числа, якщо одне з них утричі більше за інше.
Розв’язання
1 спосіб
Нехай менше число дорівнює х, а утричі більше число дорівнює 3х. Складаємо рівняння.
х + 3х = 27,2
4х = 27,2
х = 27,2 : 4
х = 6,8 – менше число;
6,8 • 3 = 20,4 – більше число.
2 спосіб
1) 1 + 3 = 4 (ч.) – всього частин;
2) 27,2 : 4 = 6,8 – менше число;
3) 6,8 • 3 = 20,4 – більше число.
3 спосіб
1) 1 + 3 = 4 (ч.) – всього частин;
2) 27,2 : 4 = 6,8 – менше число;
3) 27,2 – 6,8 = 20,4 – більше число.
Відповідь: 20,4; 6,8.
Завдання 1814
Мотузку завдовжки 10,6 м розрізали на три частини. Знайди їхні довжини, якщо третя частина на 0,4 м довша як за першу, так і за другу.
Розв’язання
1 спосіб
Нехай довжина першої частини мотузки дорівнює х м і довжина другої частини мотузки дорівнює х м, тоді довжина третьої частини — (х + 0,4) м. Складаємо рівняння.
х + х + (х + 0,4) = 10,6
3х + 0,4 = 10,6
3х = 10,6 – 0,4
3 х = 10,2
х = 10,2 : 3
х = 3,4 (м) – довжина окремо першої і другої частин мотузки;
3,4 + 0,4 = 3,8 (м) – довжина третьої частини мотузки.
2 спосіб
Нехай довжина третьої частини мотузки дорівнює х м, тоді довжина першої частини дорівнює (х – 0,4) м і довжина другої частини — (х – 0,4) м. Складаємо рівняння.
х + (х – 0,4) + (х – 0,4) = 10,6
3х – 0,8 = 10,6
3х = 10,6 + 0,8
3 х = 11,4
х = 11,4 : 3
х = 3,8 (м) – довжина третьої частини мотузки;
3,8 – 0,4 = 3,4 (м) – довжина окремо першої і другої частин мотузки.
Відповідь: 3,4 м; 3,4 м; 3,8 м.
Завдання 1815
Власна швидкість катера у 13 разів більша за швидкість течії. Рухаючись за течією 2,5 год, катер подолав 63 км. Знайди власну швидкість катера і швидкість течії.
Розв’язання
1 спосіб
Нехай швидкість течії річки дорівнює х км/год, тоді власна швидкість катера — 13х км/год. Складаємо рівняння.
(х + 13х) • 2,5 = 63
14х • 2,5 = 63
35х = 63
х = 63 : 35
х = 1,8 (км/год) – швидкість течії річки;
1,8 • 13 = 23,4 (км/год) – власна швидкість катера.
2 спосіб
1) 63 : 2,5 = 25,2 (км/год) – швидкість катера за течією річки;
2) 1 + 13 = 14 (ч.) – всього частин;
3) 25,2 : 14 = 1,8 (км/год) – припадає на 1 частину або швидкість течії річки;
4) 1,8 • 13 = 23,4 (км/год) – власна швидкість катера;
3 спосіб
1) 63 : 2,5 = 25,2 (км/год) – швидкість катера за течією річки;
2) 1 + 13 = 14 (ч.) – всього частин;
3) 25,2 : 14 = 1,8 (км/год) – припадає на 1 частину або швидкість течії річки;
4) 25,2 – 1,8 = 23,4 (км/год) – власна швидкість катера;
Відповідь: 23,4 км/год; 1,8 км/год.
Завдання 1816
З двох станцій, відстань між якими дорівнює 385 км, вирушили одночасно назустріч один одному два поїзди і зустрілися через 2,5 год. Знайди швидкість кожного з них, якщо швидкість одного в 1,2 раза більша за швидкість другого.
Розв’язання
1 спосіб
Нехай швидкість першого поїзда дорівнює х км/год, тоді швидкість другого поїзда — 1,2х км/год. Складаємо рівняння.
(х + 1,2х) • 2,5 = 385
2,5х + 3х = 385
5,5х = 385
х = 385 : 5,5
х = 70 (км/год) – швидкість першого поїзда;
1,2 • 70 = 84 (км/год) – швидкість другого поїзда.
2 спосіб
1) 385 : 2,5 = 154 (км/год) – швидкість зближення;
2) 1 + 1,2 = 2,2 (ч.) – всього частин;
3) 154 : 2,2 = 70 (км/год) – припадає на 1 частину або швидкість першого поїзда;
4) 70 • 1,2 = 84 (км/год) – швидкість другого поїзда.
3 спосіб
4) 154 – 70 = 84 (км/год) – швидкість другого поїзда.
1) 385 : 2,5 = 154 (км/год) – швидкість зближення;
2) 1 + 1,2 = 2,2 (ч.) – всього частин;
3) 154 : 2,2 = 70 (км/год) – припадає на 1 частину або швидкість першого поїзда;
Відповідь: 70 км/год; 84 км/год.
Завдання 1817
Сума довжини і ширини прямокутника дорівнює 9,6 см, причому ширина складає 3/5 від довжини. Знайди площу і периметр прямокутника.
Розв’язання
Нехай довжина прямокутника дорівнює х см, тоді ширина, що складає 3/5 (або 0,6) довжини, дорівнює 0,6х см. Складаємо рівняння.
1 спосіб
х + 0,6х = 9,6
1,6х = 9,6
х = 9,6 : 1,6
х = 6 (см) – довжина прямокутника;
6 • 0,6 = 3,6 (см) – ширина прямокутника;
Р = (6 + 3,6) • 2 = 19,2 (см) – периметр прямокутника;
S = 6 • 3,6 = 21,6 (см²) – площа прямокутника.
2 спосіб
1) 5 – 3 = 2 (ч.) – на стільки частин більша довжина;
2) 3 + 2 = 5 (ч.) – припадає на довжину;
3) 5 + 3 = 8 (ч.) – припадає на суму довжини і ширини, що дорівнює 9,6 см;
4) 9,6 : 8 = 1,2 (см) – припадає на 1 частину;
5) 1,2 • 3 = 3,6 (см) – ширина прямокутника;
6) 1,2 • 5 = 6 (см) – довжина прямокутника;
7) Р = (6 + 3,6) • 2 = 19,2 (см) – периметр прямокутника;
8) S = 6 • 3,6 = 21,6 (см²) – площа прямокутника.
Відповідь: 21,6 см²; 19,2 см.
Завдання 1818
Довжина однієї сторони трикутника складає 2/7 від периметра, а довжина іншої сторони — 3/7 від периметра. Знайди довжини цих двох сторін, якщо третя сторона завдовжки 10,4 см.
Розв’язання
1 спосіб
Нехай периметр трикутника дорівнює х см , тоді перша сторона — 2/7 х см, друга сторона — 3/7 х см, трета сторона — 10,4 см. Складаємо півняння.
2/7 х + 3/7 х + 10,4 = х
5/7 х + 10,4 = х
х – 5/7 х = 10,4
7/7 х – 5/7 х = 10,4
2/7 х = 10,4
х = 10,4 : 2 • 7
х = 36,4 (см) – периметр трикутника;
36,4 : 7 • 2 = 5,2 • 2 = 10,4 (см) – довжина першої сторони;
36,4 : 7 • 3 = 5,2 • 3 = 15,6 (см) – довжина другої сторони.
2 спосіб
1) 2/7 + 3/7 = 5/7 (ч.) – припадає на першу і другу сторони разом;
2) 1 – 5/7 = 7/7 – 5/7 = 2/7 (ч.) – припадає на третю сторону, що дорівнює 10,4 см.
3) 10,4 : 2 • 7 = 36,4 (см) – периметр трикутника;
4) 36,4 : 7 • 2 = 5,2 • 2 = 10,4 (см) – довжина першої сторони;
5) 36,4 : 7 • 3 = 5,2 • 3 = 15,6 (см) – довжина другої сторони.
3 спосіб
1) 2 + 3 = 5 (ч.) – припадає на першу і другу сторони разом;
2) 7 – 5 = 2 (ч.) – припадає на третю сторону, що дорівнює 10,4 см;
3) 10,4 : 2 = 5,2 (см) – припадає на 1 частину сторони;
4) 5,2 • 2 = 10,4 (см) – довжина першої сторони;
5) 5,2 • 3 = 15,6 (см) – довжина другої сторони.
Відповідь: 10,4 см; 15,6 см.
Завдання 1819
Юля прочитала спочатку 0,25 усієї книжки, а потім ще 0,4 решти, після чого виявилося, що вона прочитала на 30 сторінок більше, ніж їй залишилося прочитати. Скільки сторінок у книжці?
Розв’язання
1 спосіб
Нехай у книжці х сторінок. Спочатку Юля прочитала 0,25х сторінок, тоді решта
становить х – 0,25х = 0,75х сторінок. Потім вона прочиталв ще 0,4 решти, тобто
0,4 • 0,75х = 0,3х сторінок. А всього прочитала 0,25х + 0,3х = 0,55х сторінок,
тоді їй залишилося прочитати х – 0,55х = 0,45х сторінок, різниця яких дорівнює 30.
Складаємо рівняння:
0,55х – 0,45х = 30
01х = 30
х = 30 : 0,1
х = 300
2 спосіб
1) 1 – 0,25 = 0,75 (книжки) – решта, що становить 0,4 (або 4/10);
2) 0,75 : 10 • 4 = 0,075 • 4 = 0,3 (книжки) – прочитала потім;
3) 0,25 + 0,3 = 0,55 (книжки) – прочитала всього;
4) 1 – 0,55 = 0,45 (книжки) – залишилося прочитати;
5) 0,55 – 0,45 = 0,1 (книжки) – на стільки більше прочитала, що дорівнює 30 с.
6) 0,1 : 30 = 300 (с.)
Відповідь: у книжці 300 сторінок.
Завдання 1820
|
m = 1,17 : 0,9 = 1,3
h = 2,13 – m = 2,13 – 1,3 = 0,83
g = 0,79 + h = 0,79 + 0,83 = 1,62
n = g : 1,62 = 1,62 : 1,8 = 0,9
k = 1,71 : n = 1,71 : 0,9 = 1,9
l = 10,44 – k = 10,44 – 1,9 = 8,54
|
_11,7| 9 9 1,3 _21 21 0 |
+0,79
0,83
1,62
|
_16,2| 18 162 0,9 0 |
_17,1| 9 9 1,9 _81 81 0 |
_10,44
1,90
8,54
|
Завдання 1821
У трьох ящиках разом 62,88 кг товару. У першому ящику товару в 1,4 раза більше, ніж у другому, а у третьому — стільки, скільки його в першому і другому разом. Скільки кілограмів товару в кожному ящику?
Розв’язання
Нехай у другому ящику х кг товару, тоді у першому — 1,4х кг, в третьому — х + 1,4х кг. Складаємо рівняння.
1,4х + х + (х + 1,4х) = 62,88
4,8х = 62,88
х = 62,88 : 4,8
х = 13,1 (кг) – товару в другому ящику;
13,1 • 1,4 = 18,34 (кг) – товару в першому ящику;
13,1 • 2,4 = 31,44 (кг) – товару в третьому ящику.
Відповідь: 18,34 кг; 13,1 кг; 31,44 кг.
Завдання 1822 Письмове додавання і письмове віднімання
|
1) +5452319
3452317
8904636
|
+ 7352419
3452317
10804736
|
+ 8311152
3452317
11763469
|
|
2) _10311153
1452317
8858836
|
_7452318
1452317
6000001
|
_9352421
1452317
7900104
|
|
а)
|
б)
|
в)
|
|
8 904 636 > 6 000 001
|
10 804 736 > 7 999 104
|
11 763 469 > 8 858 836
|
Завдання 1823 Письмове множення і письмове ділення
|
× 4211
273
12633
29477
8422
1149603
|
x 5317
273
15951
37219
10634
1451541
|
x 6002
273
18006
42014
12004
1638546
|
|
2) _76072 | 37
74 2056 _207 185 _222 222 0 |
_58386 | 37 37 1578 _213 185 _288 259 296 296 0 |
_48359 | 37 37 1307 _113 111 _259 259 0 |
|
3) Порівняй:
|
||
|
_1149603
1578
1148025
|
_1638546
2056
1636490
|
+1451541
1307
1452848
|
|
а) 1 148 025 < 1 636 490
|
а) 1 452 848 < 1 638 546
|
|
Завдання 1824
Один з робітників виготовив 96 деталей за 6 год, а інший — 45 деталей за 2,5 год. За скільки годин вони виготовлять 119 деталей, працюючи разом?
Короткий запис
I — 96 д. — 6 год
II — 45 д. — 2,5 год
Разом — 119 д. — ?
Розв’язання
1) 96 : 6 = 16 (д.) – виготовив перший робітник за 1 год;
2) 45 : 2,5 = 18 (д.) – виготовив другий робітник за 1 год;
3) 16 + 18 = 34 (д.) – виготовили два робітники разом за 1 год;
4) 119 : 34 = 3,5 (год) – час виготовлення 119 деталей, працюючи разом.
Відповідь: за 3,5 год.
Завдання 1825
У родині Максименків батько заробляє 12 000 грн на місяць, мати — 14 000 грн, а старший син–студент отримує 3000 грн стипендії та ще 2000 грн, підробляючи як фрилансер (freelancer — вільний робітник). Який бюджет цієї родини: 1) на місяць; 2) на квартал (3 місяці); 3) на рік?
Розв’язання
1) 12000 + 14000 + 3000 + 2000 = 26000 + 5000 = 31000 (грн) – бюджет на місяць;
2) 31000 • 3 = 93000 (грн) – бюджет на квартал (3 місяці);
3) 31000 • 12 = 372000 (грн) – бюджет на рік.
Відповідь: 31000 грн; 93000 грн; 372000 грн.
Завдання 1826
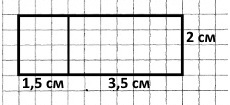
Накресли на аркуші в клітинку прямокутник зі сторонами 2 см і 1,5 см. Доповни його до такої фігури, щоб площа прямокутника становила 3/10 від площі цієї фігури.
Розв’язання
1) 2 • 1,5 = 3 (см²) – площа прямокутника;
2) 3 : 3 • 10 = 10 (см²) – площа фігури;
3) 10 : 2 = 5 (см) – довжина фігури;
4) 5 – 1,5 = 3,5 (см) – на стільки треба продовжити сторону 1,5 см прямокутника.